Health and homelessness in Scotland: research

Annex E: Temporal analysis: health activity relative to the date of first homelessness assessment

In order to perform the temporal analysis the date of the health activity needs to be considered. The date of health activity itself is not primarily of interest. What is of interest is when the health activity occurred relative to when that person became homeless. The date of the first homelessness assessment will be used as a proxy for the date of becoming homeless. The date of the first homelessness assessment can then be subtracted from the date of the start of the health activity (if an episode), or simply the date of health activity. Positive values will indicate health activity that occurs after the homelessness assessment, negative values indicate health activity prior to the homelessness assessment. Any activity that happens at the same time will have a value of zero. Thus t _r = t _he - t _ho, where t _he is the time of the health activity and t _ho is the time of the first homelessness assessment.

We can therefore plot activity as a function of the relative time t _r. The structure of this plot will not only be dependent on the direction of causality with respect to the homelessness episode. It will also depend on the relative timing of the availability of the data. Even if health activity rate and the rate of homelessness assessments were constant over time, there would still be variation seen in activity over t _r. For example, suppose that health data covered the period from the start of 2011 to the start of 2017, and homelessness data went from 2002 to 2015 (see Figure E.1). The range of t _r would then be from -4 to 15 years. Activity could happen at t _r = -4 if there was someone who had a homelessness assessment at the start of 2015 and had a health episode at the start of 2011 (indicated by the arrow (A) on Figure E.1). It would not be possible for t _r < -4 as this would require either that the homelessness assessment happened later than this, or the health activity happened earlier than this, neither of which are possible given the availability of data. Similarly the maximum possible value of t _r = 15, as indicated by the arrow (B) on Figure E.1. In general then t _r,max = t _he,max- t _ho,min, and t _r,min = t _he,min - t _ho,max, where max and min indicate the largest and smallest possible values given the data available. Therefore the range of ( i.e. the difference between its maximum and minimum values) is given by:

t _r,range = t _r,max - t _r,min

= ( t _he,max - t _ho,min) - ( t _he,min - t _ho,max)

= t _he,max - t _he,min + t _ho,max - t _ho,min

= t _he,range + t _ho,range

In this case the range would be 19 years, which is the sum of the range of the homelessness data (6 years) and that of the health data (13 years).

Figure E.1: Impact of different time periods in datasets on calculating the date relative to the first homelessness assessment

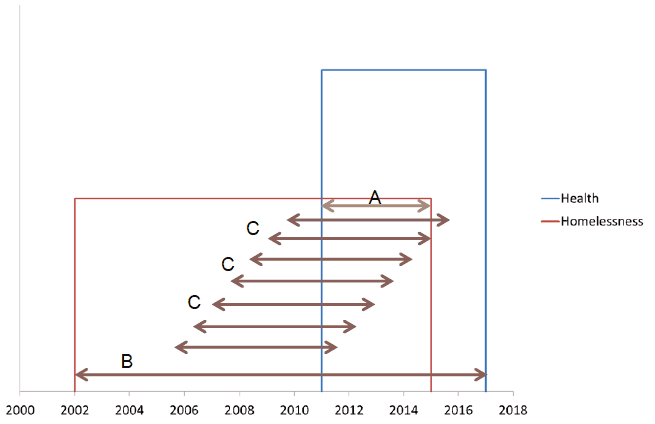
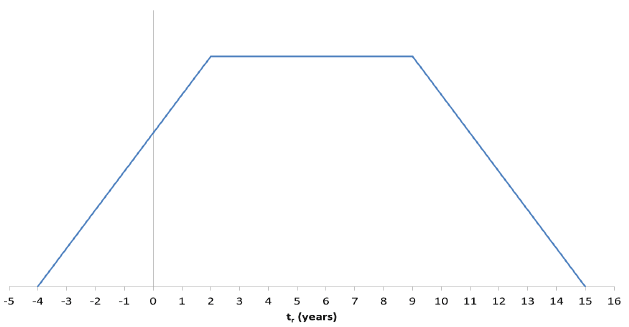
It can also be seen that the amount of activity that happens will not be constant over this range. For example there is only one possible combination of dates that will result in years. However there are many possible dates that result in years, as indicated by the multiple arrows (C) in Figure E.1. In general the number of possible combinations of dates that leads to particular values of will increase as diverges from its maximum and minimum values. Eventually this increase will stop and the number of combinations will remain constant. For example if we imagine the orange arrows in Figure E.1 being extended to the left slightly then there would be a similar number of combinations as there are for the orange arrows themselves. Therefore plotting the number of possible combinations of dates over would result in the plot in Figure E.2. This is also the graph that would be seen when plotting the count of health episodes as a function of if the rates of homelessness assessments were constant over times, and the rate of health episodes were constant over time for these people.

Figure E.2: Theoretical shape of the count of health activity episodes relative to the date of first homelessness assessment

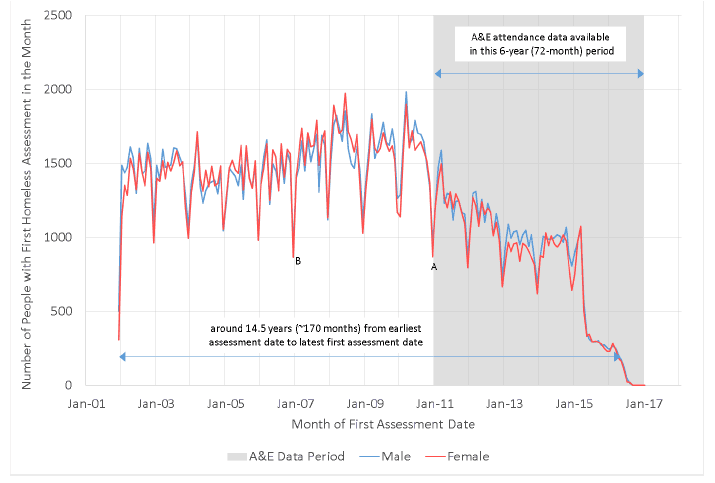
In this way the resulting pattern would be the convolution ^[71] of the health data and the homelessness data. In the actual analysis the shape will be complicated further by variations in the number of events over time. Figure E.3 below shows the actual distribution of the number of people with homelessness assessments in each month over the time period (along with the time period of the A&E dataset for reference). It can be seen that this is not constant. There is significant seasonality with fewer homelessness assessments in December of each year. Furthermore there are fewer homelessness assessments each year after 2011 than there were before then. This will make the trend of the health activity as a function of even more complex than that seen in Figure E.2.

Figure E.3: Number of Homeless People by Month of First Homeless Assessment

There will also be variations in the health activity rates that will not be related to the homelessness episode. For example it may be that health activity rates increase over time as people age. This would make the trend increase with as each person included would have more activity at later times than at earlier times.

Fortunately it is possible to control for both these effects to more clearly isolate the relationship between homelessness and health activity. To do this we make use of the controls. For each person in the EHC there are two controls with the same age who are known to be alive [although not necessarily present in the Scottish population] at the date of the EHC person's first homelessness assessment. We therefore use the date of first assessment of the EHC person and assign this to each of the two controls. Using this date a value of can be calculated for all the activity of the controls. These people will therefore have exactly the same range of possible values of as the EHC people. Furthermore, these controls are the same age as the people in the EHC. Therefore the effects of the convolution of the datasets and of the aging cohort will affect the EHC and the controls equally.

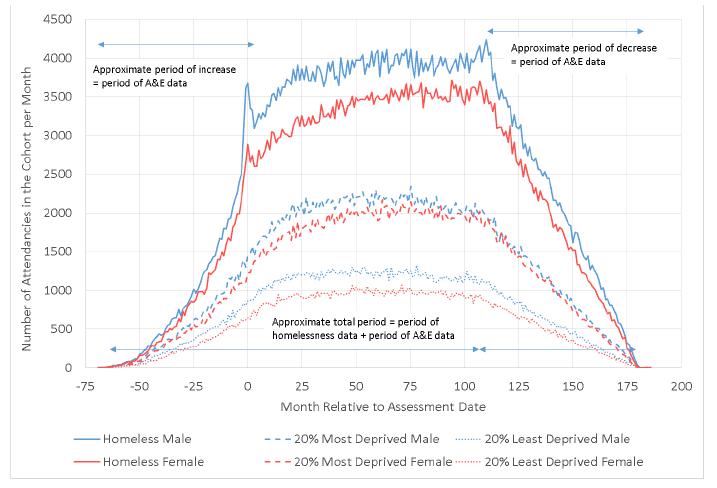
As an example, Figure E.4 shows what happens when this temporal analysis is performed on the homelessness data and the is below that when this is done the rough shape of the trend is similar across the cohorts. Therefore we divide the values seen in the EHC by those seen in the LDC. This would divide out the shape of the trend simply due to these effects, making it much flatter. Whatever structure remains would therefore be more directly related to the homelessness itself.

In some cases the activity levels among the LDC may fluctuate substantially from month to month. This is especially the case for activity relating to services that are less used by people in the LDC. To avoid carrying that fluctuation in to the ratios the LDC values are smoothed before being used as a denominator. To do this a triangular smoothing kernel was used, with a width of 20 months.

Figure E.4: A&E Attendances per month relative to first assessment date by cohort: