The Scottish Shelf Model. Part 2: Pentland Firth and Orkney Waters Sub-Domain
Part 2 of the hydrodynamic model developed for Scottish waters.
5 Marine Energy Resources
5.1 Introduction
According to the Invitation to Tender ( ITT) Deliverable CS 1(b) requires that a one-year simulation using idealized forcing is undertaken for waves. As shown in the previous section, the year 2005 has been chosen as the representative year. The results from the simulation of the representative year (2005) are used to map the available wave energy resources in the Pentland Firth and Orkney waters ( PFOW). In addition, the tidal energy resources have been calculated. Mean neap and spring tidal range and mean neap and spring peak currents were calculated from the M2 and S2 tidal constituents. Tidal power density was calculated using the annual results from the climatological simulation.
5.2 Tidal energy resources
There are two main approaches to estimating tidal energy resources - either to select a representative tidal period (typically a "mean" spring tide) to analyse, or to perform harmonic analysis on a longer time series and use the constituents derived to compute representative values. The former approach is outlined in the EMEC standards document "Assessment of Tidal Energy Resource" ( www.emec.org.uk), whilst the latter approach was used for the ABPMer / NOC Atlas of Marine Energy Resources ( www.renewables-atlas.info). The second approach, performing harmonic analysis of a longer time series was chosen in this study.
The PFOW model was run for a whole year with boundary conditions taken from the shelf model climatology run. The results from this run were then analysed. The MATLAB software package T_TIDE was used to analyse time series to obtain harmonic constituents.
5.2.1 Mean Spring / Neap Tidal Range
Mean spring tidal ranges have been computed directly from the two principal semi-diurnal components M 2 and S 2 based on the following equations from Pugh (1987):
mean high-water springs = Z 0 + (H M2 + H S2)
mean low-water springs = Z 0 - ( H M2 + H S2)
spring tidal range = mean high-water springs - mean low-water springs
Values for these constituents were obtained from a harmonic analysis of 60 days' worth of data from the PFOW climatology run. These harmonic components control the timing of the spring-neap cycle, and their combination is considered to give a good measure of average spring (and neap) tides. The data was also used to calculate the mean neap tidal range as:
mean high-water neaps = Z 0 + (H M2 - H S2)
mean low-water neaps = Z 0 - (H M2 - H S2)
neap tidal range = mean high-water neaps - mean low-water neaps
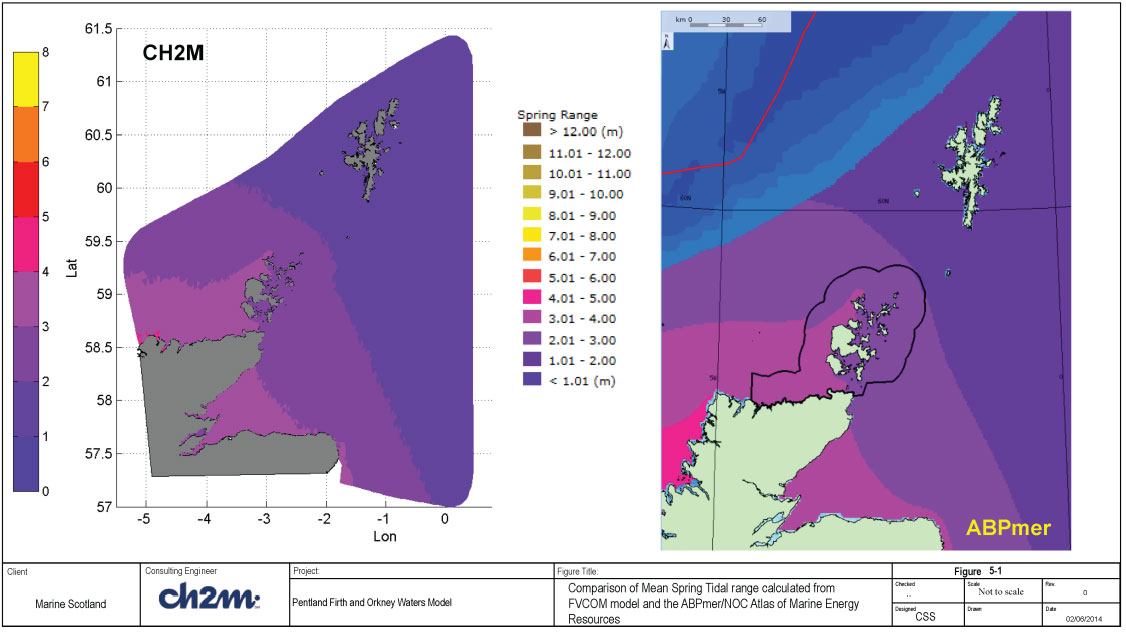
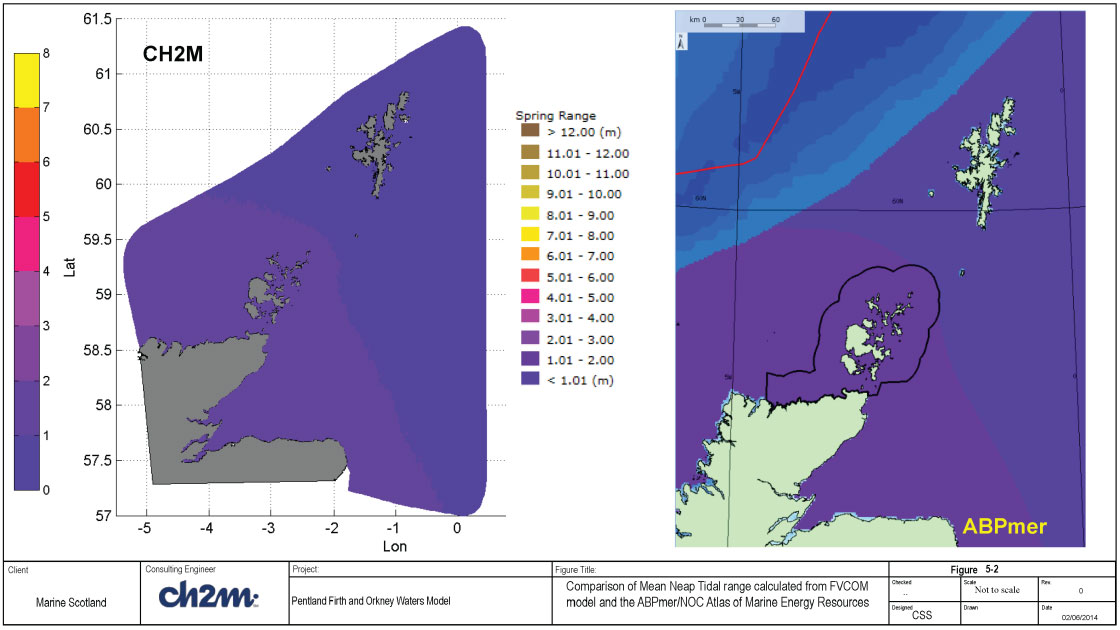
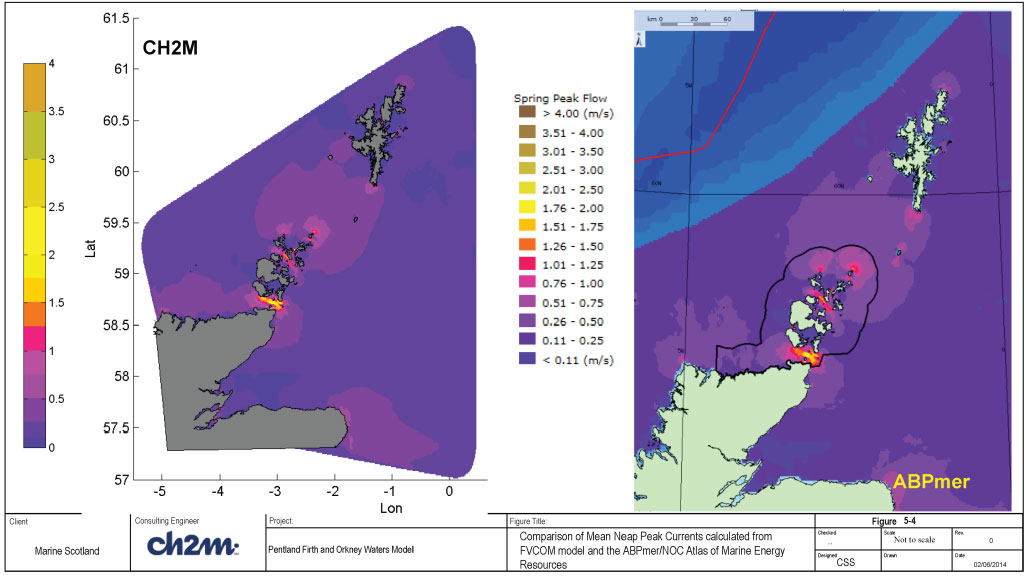
A map of the mean spring results are shown, along with the equivalent tidal range from the ABPMer / NOC Atlas of Marine Energy Resources ( http://www.renewables-atlas.info/), in Figure 5-1. The corresponding plots for mean neap tidal range are shown in Figure 5-2. There are some small variations in spring tidal range between the ABPMer/ NOC Atlas and the CH2MHILL data sets, the reduction in tidal range with distance from the mainland occurs sooner in the CH2MHILL data along the east coast; although it should be noted that the Lochs within the Moray Firth are resolved and included within the PFOW model, but do not appear to be resolved within the ABPMer / NOC Atlas results. Overall the agreement between the two data sets is good. The comparison of neap tides shows very good agreement between the two data sets.
5.2.2 Mean Spring / Neap Currents
Mean peak current speeds have been calculated from a harmonic analysis of 60 days of tidal velocities, from the PFOW climatology run. In line with the methodology used for the ABPMer / NOC Atlas, a mid-depth velocity was used for the calculations. The east and west components of velocity were analysed using T_TIDE to give the M 2 and S 2 amplitudes and phases. These were in turn analysed to give the semi-major axis amplitudes for each ellipse. The mean peak spring current was then computed as:
mean peak spring current = amplitude semi-major axis M 2 + amplitude semi-major axis S 2
The mean neap spring current was computed as:
mean peak neap current = amplitude semi-major axis M 2 - amplitude semi-major axis S 2
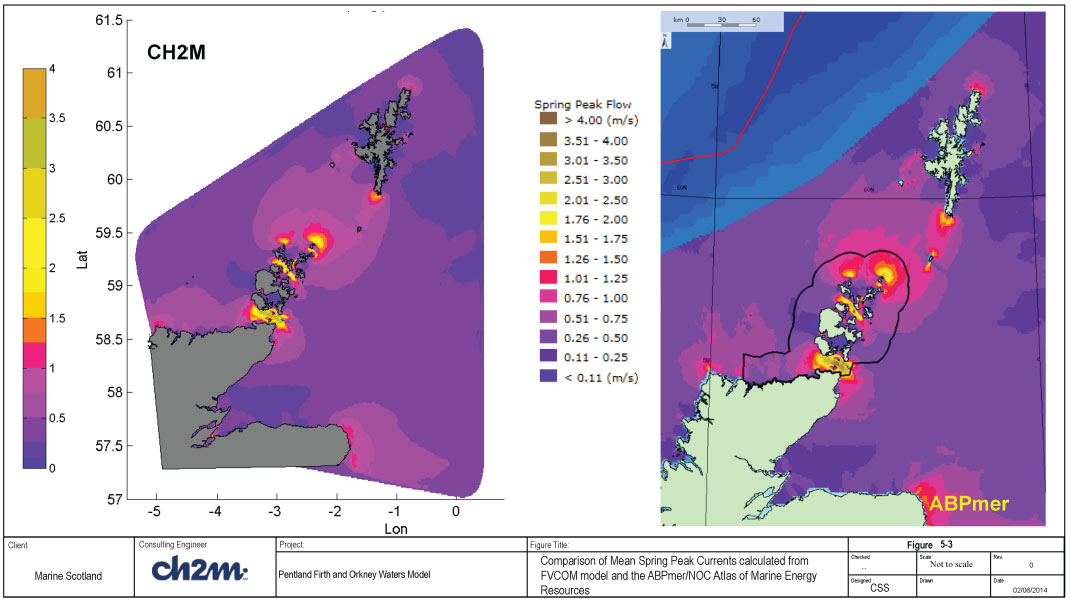
A map of the results for mean spring current is shown, along with the equivalent peak currents from the ABPMer / NOC Atlas of Marine Energy Resources, in Figure 5-3. Corresponding plots for the mean neap current are shown in Figure 5-4. The comparison of peak flows show good agreement between the data sets. Spatial variations are consistent between the two data sets for both the spring and neap tides, however the CH2MHILL data gives lower values of peak flow velocities at some locations, i.e. Fair isle (between Orkney and Shetland) and the north east corner of the mainland.
5.2.3 Mean Tidal Stream Power Density
The mean tidal stream power density (denoted as P TS) is the kinetic energy in the tidal flows (per unit cross-sectional area) averaged over the time period, which in this exercise was 365 days of the PFOW climatology run. A mid-depth velocity was used as in the previous section, with the mean power density being given by:
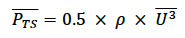
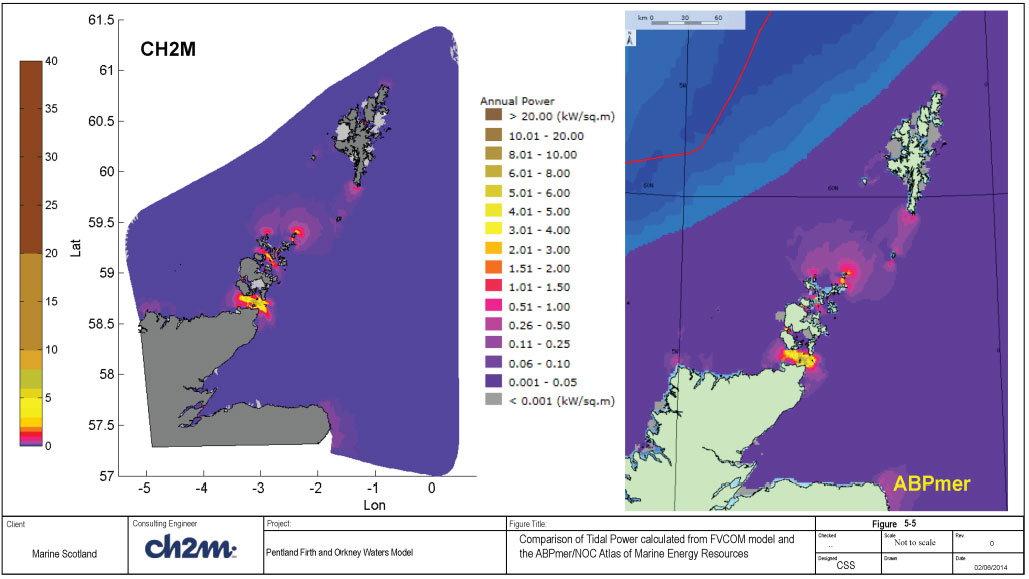
Where U is the mid-depth current speed, P is density taken as 1027 kg/m 3 and the overbar sign denotes averaging over the entire year. A map of the results is shown, along with the equivalent tidal power from the ABPMer / NOC Atlas of Marine Energy Resources, in Figure 5-5. As with the spring and neap peak flows the spatial variations in tidal stream power are consistent between the two data sets but the CH2MHILL data gives lower values at some locations.
5.3 Wave energy resources
The model results from the wave simulations for the representative year described in Section 4 were processed to determine maps of the following wave energy parameters at the project site:
- Mean annual parameters
- Mean annual significant wave height, H m0 (m)
- Mean annual peak wave period, T p (s)
- Mean annual wave power, P (kW/m)
- Mean seasonal wave power, P (kW/m)
- Mean monthly wave power, P (kW/m)
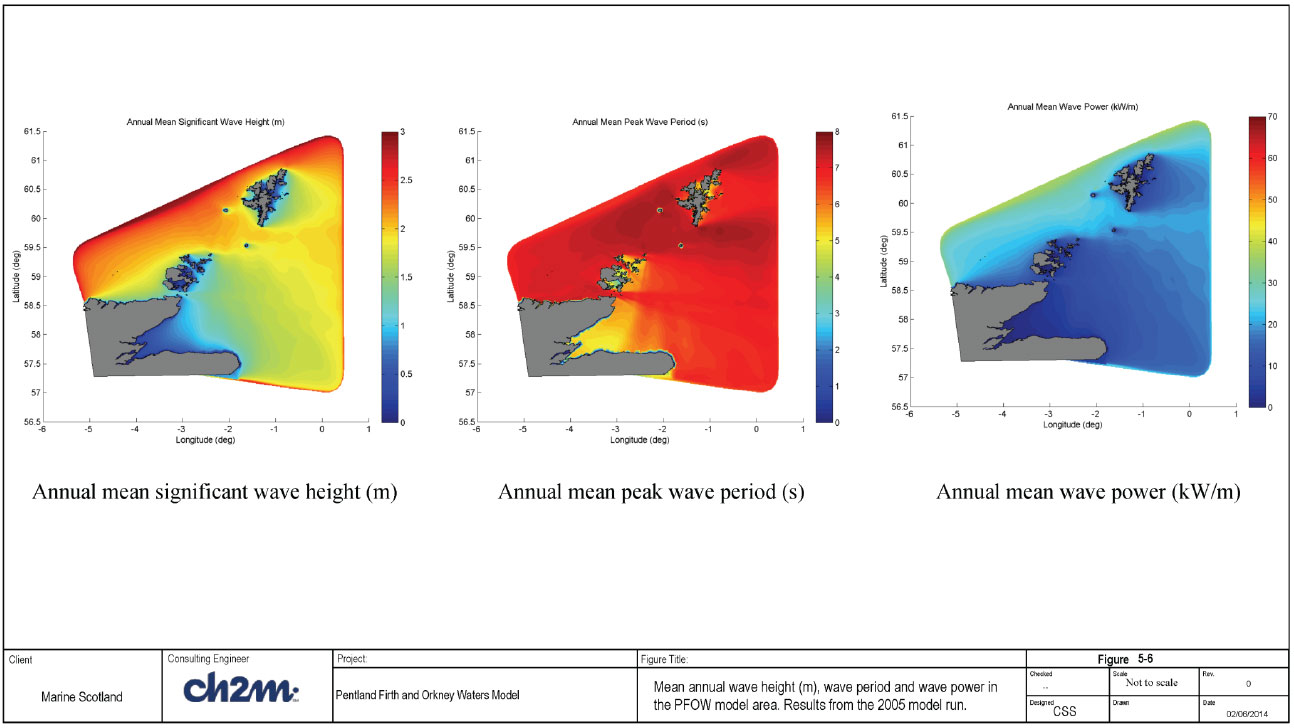
The mean annual parameters are shown in Figure 5-6. As discussed in Section 4.4.1, the mean monthly wave power has been determined by scaling the wave power results calculated for the each month in 2005 with the corresponding R value to determine the long term monthly wave power. The maps showing the wave energy parameters are shown in Appendix E (E1 -E5). The results from this study are compared with previous studies in Section 5.3.3 ( ABPmer, 2008 and 2012) and 5.3.4 (Neill et al, 2014).
In addition to the wave power maps, the following wave energy parameters were calculated at selected stations (see Table 4-12 for a list of the stations) and presented in Appendix E (Figure E5-E16).
- Annual wave power weighted rose
- Annual wave power exceedance curve
- Monthly distribution of wave power
- Scatter plot of Hm0-Te
Wave power is not one of the output parameters from FVCOM- SWAVE model. Hence, this parameter needs to be calculated separately. Matlab scripts were developed to carry out these calculations. There are two methods to calculate wave power namely: 1) the direct method using wave spectra and 2) the approximate method using wave parameters. These methods are described in Section 5.3.1 and 5.3.2. In FVCOM- SWAVE, wave spectra is not output over the entire model domain. Hence, only the approximate method can be used to output the wave power over the domain. However, it is possible to output the frequency spectrum at specific points in the model area, which can in turn be used to determine the wave power at those points.
5.3.1 Calculation of wave power from wave spectrum
The omni-directional wave power, P (W/m) can be calculated from the wave spectrum using ( EMEC, 2009):
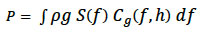(5-1)
In Eq 5-1, is the density of seawater (1025 kg/m 3), g is acceleration due to gravity (9.81m/s), S is the energy spectral density (as a function of frequency, f), C g is the wave group velocity (calculated using the linear wave dispersion equation. Given the frequency, f i and spectral density, S i at N discrete frequency points, Eq 5.1 can be expressed in discrete form to calculate wave power as shown below:
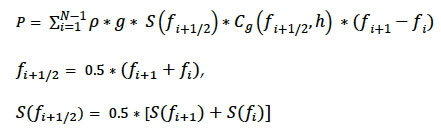(5-2)
C g is calculated using frequency f i+1/2 and water depth, h.
In addition to calculating the wave power, the spectral data can also be used to determine the appropriate relationship between the peak period and other integral wave periods, T -10 (=m -1/m 0), T 01 (=m 0/m 1) and T 02 (=sqrt(m 0/m 2). T -10 is the wave energy period (T e) used in the calculation of wave energy from wave parameters, T 01 is sometimes called the mean wave period, while T 02 is the approximately the zero-crossing wave period (T z). The n th moment of the spectrum is:
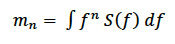(5-3)
And in discrete form:
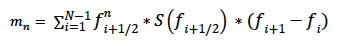(5-4)
5.3.2 Calculation of wave power from parameters
The omni-directional wave power can be calculated using integral wave output parameters (H m0 and T e) as shown below:
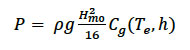(5-5)
where H m0 is the significant wave height, C g is the wave group velocity (calculated as a function of wave energy period, T e and water depth, h). In deep water (water depth > L 0/2, where L 0 is deep water wave length) Eq. 5.5 can be further simplified to:
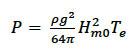(5-6)
As the bathymetry in the study area includes shallow to transitional water depths, Eq 5-5 was used to calculate the wave power over the entire model area.
FVCOM- SWAVE outputs the peak wave period, but does not output the wave energy period T e. In order to determine T e, the spectral output data at the selected stations were analysed to determine the moments of the spectrum and spectrally derived wave periods T e, T 01 and T 02 as described in Section 5.3.1. Furthermore, the ratios T p/T e, T p/T 01, T p/T 02 were calculated at every output time step (typically 1-hour) and averaged over the entire year (see Table 5-1). At the exposed locations, T p/T e vary from 1.13 to 1.17 with an average of 1.14. The corresponding average T p/T 01 and T p/T 02 is 1.26 and 1.34. These ratios correspond approximately to a JONSWAP spectral shape with peakedness parameter of 1.9. The wave energy period T e used in the power calculations is calculated from the calculated peak periods (T p) using the average ratio T p/T e = 1.14. Table 5.2 shows a comparison of the empirically derived ratios used in this study with those used in previous wave power studies at the project site.
Table 5-1 Spectrally derived wave period ratios at the output locations (Each ratio is averaged over simulated year).
| Location ID |
T p/T e |
T p/T 01 |
T p/T 02 |
|---|---|---|---|
| WN1a |
1.15 |
1.26 |
1.34 |
| WN2a |
1.13 |
1.25 |
1.32 |
| WN2b |
1.15 |
1.27 |
1.35 |
| WN3a |
1.16 |
1.28 |
1.37 |
| WN3b |
1.17 |
1.31 |
1.39 |
| Billia Croo East buoy |
1.13 |
1.24 |
1.31 |
| Billia Croo Offshore |
1.13 |
1.24 |
1.31 |
| Costa Head |
1.14 |
1.25 |
1.33 |
| Average |
1.14 |
1.26 |
1.34 |
| Falls of Wareness |
1.20 |
1.35 |
1.45 |
| West PF |
1.16 |
1.30 |
1.38 |
| Mid PF |
1.15 |
1.28 |
1.36 |
| East PF |
1.21 |
1.37 |
1.47 |
Table 5-2 Empirically derived Period ratios
| Location ID |
Empirical ratios |
Remarks |
|---|---|---|
| ABPme |
T e/T z = T e/T 02 =1.05 - 1.14 |
|
| ABPme |
T e/T m = T e/T 01 = 1.19 |
|
| Present study |
T p/T e = 1.14; |
|
5.3.3 Comparison with ABPmer results
The results from this study are compared with results from ABPmer (2008, 2012) in Appendix E (Figure E-17 to Figure E-22). The ABPmer (2008) study was used to develop a wave and tidal energy Atlas UK waters. The ABPmer (2012) study supplements this study with a high resolution model of the PFOWSA. In the present report, the ABPmer (2012) PFOWSA results is referenced as ABPmer ( PFOW), while the original study for the UK Atlas is referenced as ABPmer (Shelf). In order to better illustrate the differences between the present study and ABPmer studies, the wave height and wave power are also compared at selected locations (see Table 4-10 for a list of selected locations).
The comparison plots in Appendix E show the following features:
- Model bathymetry - The main bathymetry features in both models are broadly similar (Figure E-17). The present model shows more detailed features than the 12km grid bathymetry used in ABPmer (2008). For example, the depths in the 12km grid tend to be deeper near the coast. This is expected, since the 12km grid model does not resolve the variation in the water depths close to the coast. The consequence of the increased depths in the 12km grid model is that the wave height and wave group velocity are likely to be overestimated near the coast, so that the corresponding wave power is also likely to be high.
We were not able to access plots of the PFOWSA area bathymetry used in ABPmer (2012), and therefore unable to compare with the high resolution bathymetry used in the present study.
- Wave height - The spatial distribution of the mean annual significant wave height is broadly similar for the two model results. The wave heights are higher on the western side (North Atlantic side) and lower in the lee of Orkney, Shetland, the Pentland Firth and the Moray Firth. The mean annual wave height is lower (about 0.3m) in the present model compared to the ABPmer (Shelf) results, and about 0.5m lower compared to the ABPmer ( PFOW) results.
Figures E-18 and E-19 show that the ABPmer ( PFOW) results are higher compared with the ABPmer (Shelf) results. The reasons for this are unclear. Possible reasons include: a) use of boundary wave data from a model that is different from the Met Office UK Waters model in the ABPmer ( PFOW) model; b) Rougher wave conditions in the additional period outside of June 2000-May 2007 used in the original study; and c) differences in the model resolution and model setup. The boundary conditions for this study was obtained from the Met Office wave data, which was used in the ABPmer (2008) study. It is therefore considered prudent to focus only on comparing the present results with the ABPmer (2008 results).
We conclude that the present model provides a reasonably accurate representation of the wave height variation in the study area, as this is based on a larger high resolution model that has been calibrated and validated for this model area.
- Wave period - The mean annual peak wave period in the present model is generally lower (about 2secs) compared to the ABPmer (2008) results. The reason for this is unclear. Possible reasons are: a) the influence of swell wave conditions at the boundary of the present model. In the present model, wave parameters have been specified at the model boundary and a JONSWAP spectral shape prescribed. Such a spectral shape will not include the effect of mixed wind sea and swell waves correctly, and may lead to smaller peak wave period. However, this is the best approximation that can be made within the framework of the present study, as only the wave parameters were available as offshore boundary data; b) the method of calculation of peak period (T p) from the spectral data. The peak period T p is defined as the wave period corresponding to the maximum spectral energy density in the wave spectrum. However, given the discrete frequencies that are used in numerical models, calculation of peak period using the direct search method means that the output peak period will have some granularity (as it can only be found at the different discrete periods). This is the method used in FVCOM- SWAVE. However, alternative methods exist to improve the accuracy of determining T p. For instance, by fitting a quadratic to the 3 values around the peak spectral density (as used in MIKE 21 SW). The method used in the Met Office Coastal wave model used in the ABPmer (2008) study is not known to us at this time.
- Wave power - The mean annual wave power in the present model is generally similar or lower to the ABPmer (Shelf) results. This is probably due to the differences discussed above (bathymetry, model resolution and effect of swell waves). In the present study, the bathymetry has been compiled from the best available data sources (see Section 2.2), and the mesh resolution is significantly improved compared to previous models. As the boundary data was specified with wave parameters (as opposed to wave spectrum), it is likely that the effect of swell waves may not be well represented. Even with this limitation, the wave model was successfully calibrated against measured wave heights at 3 different locations.
5.3.4 Comparison with results from Neill et al (2014)
The results from this study are compared with results from Neill et al (2014) in Appendix E (Figure E-23 to Figure E-25). Neill et al (2014) used the SWAN (Simulating WAves Nearshore) wave model with a high resolution grid (approximately 434m grid resolution) over the Pentland Firth and Orkneys Waters to quantify the Orkney wave power resource over a ten year period (2003 - 2012). The wave model validation results achieved by Neill et al (2014) is reproduced in Figure E-23, and shows that the model is adequately validated.
The comparison plots in Appendix E show the following features:
- Monthly wave power - The variation of mean monthly wave power developed in the present model is generally similar to the results of Neill et al (2014), see Figure E-24. The wave power is typically maximum in January and gradually reduces through April. Between May and August, the wave power is generally low, and starts increasing gradually again in September through December. The calculated wave power in the present model is however higher (visually estimated as about 25% higher) than the results of Neill et al (2014).
- Annual wave power - The spatial variation of the mean annual wave power developed in the present model is similar to the results of Neill et al (2014). This indicates that most of the wave power resource are on the western and northern coasts (and offshore areas) of Orkneys. However, the calculated wave power in the present model is higher (visually estimated as about 25% higher) than Neill et al (2014). Furthermore, the penetration of wave energy through the Pentland Firth does not appear to be reproduced to the same extent in the Neill et al model.
It is interesting to see that the key features of the annual and monthly wave power resource are similar in both models. However, there are differences in the level of the wave power resources. Neill et al estimated the uncertainty in their calculated mean annual wave power resources to be in the order of 15 to 20%, west of the Orkneys. Addition of the uncertainty estimate to their calculated wave power resources will bring their results closer to the results from the present study.
5.3.5 Influence of wave-current interaction
The influence of wave-current interaction can be conveniently separated into two categories - namely, 1) effect on currents on waves as summarised in Table 5-3, and 2) effect of waves on currents summarised in Table 5-3.
Table 5-3 Effect of currents on waves
| Process |
Effect |
Modelled in FVCOM (Y/N) |
|---|---|---|
| Tide levels |
|
Y - Included in wave action equation solved. |
| Current speeds |
|
Y - Included in wave action equation solved. |
Table 5-4 Effect of waves on currents
| Process |
Effect |
Modelled in FVCOM (Y/N) |
|---|---|---|
| Wave boundary layer |
Increased bottom friction by mean flow |
N |
| Stokes drift |
Modification of currents in the top layers due to wave orbital velocities. |
N |
| Radiation stresses |
Breaking waves driven currents in the surf zone. |
Y (depends on mesh resolution) |
| Mixing due to surface waves |
Changes to turbulent mixing due to surface waves |
Y -parameterised in 2.5 MY model |
In the present study, the influence of wave-current interaction on wave parameters and wave energy resources in the PFOW area has been assessed. The assessment was carried out by running two sets of simulations, namely: 1) waves only runs (with and without wind forcing) and 2) coupled wave and flow model simulation as summarised in Table 5-5. The model setup parameters for the runs are summarised in Table 5-6. These simulations were carried out using the wave model mesh, which is different (coarser) from the mesh used for the hydrodynamic simulations in Section 3.2.1. Thus, a tides only simulation was also carried out to ensure that the modelled tides using this mesh is also good.
Table 5-5 Simulations carried out to assess effect of wave-current interaction
| Run ID |
Description |
Simulation period |
Remarks |
|---|---|---|---|
| co00 |
Tide only simulation, no waves |
10 days |
Check tide levels and current speeds are reasonable when compared to measured data & previous flow model calibration. |
| wo01 |
Waves only simulation |
48h |
Baseline run, no wind forcing |
| wo02 |
Waves only simulation + wind |
48h |
Baseline run + wind forcing |
| wc01 |
Waves + tides |
48h |
Assess influence of wave-current interaction by comparison with Run wo01 |
| wc02 |
Waves + tides + wind |
48h |
Assess influence of wave-current interaction by comparison with Run wo02 |
| wc03 |
Waves + tides + wind + surface wave mixing ON. |
48h |
Assess influence of wave-current interaction by comparison with Run wo02 |
Table 5-6 model setup parameters
| Parameter |
Value |
|---|---|
| Mesh: |
23,508 nodes; 41,666 cells; |
| Time steps: |
EXTSTEP_SECONDS=0.5 , ISPLIT= 3 |
| Forcing: |
Elevation forcing + nesting data (from AMM model); |
| Turbulence physics |
Mixing: Smagorinsky+MY2.5; |
| Wave model setup parameters: |
Boundary data: Hm0=2m, Tp=10s, MWD=270degN |
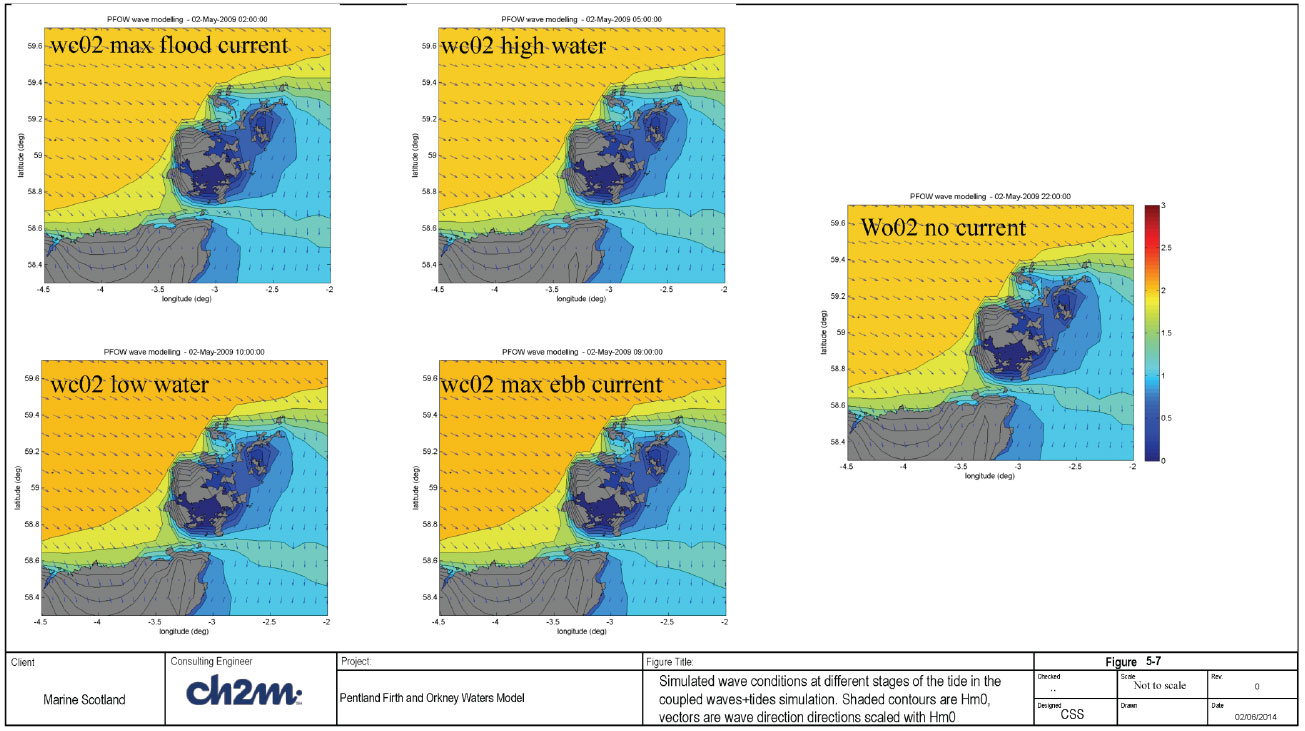
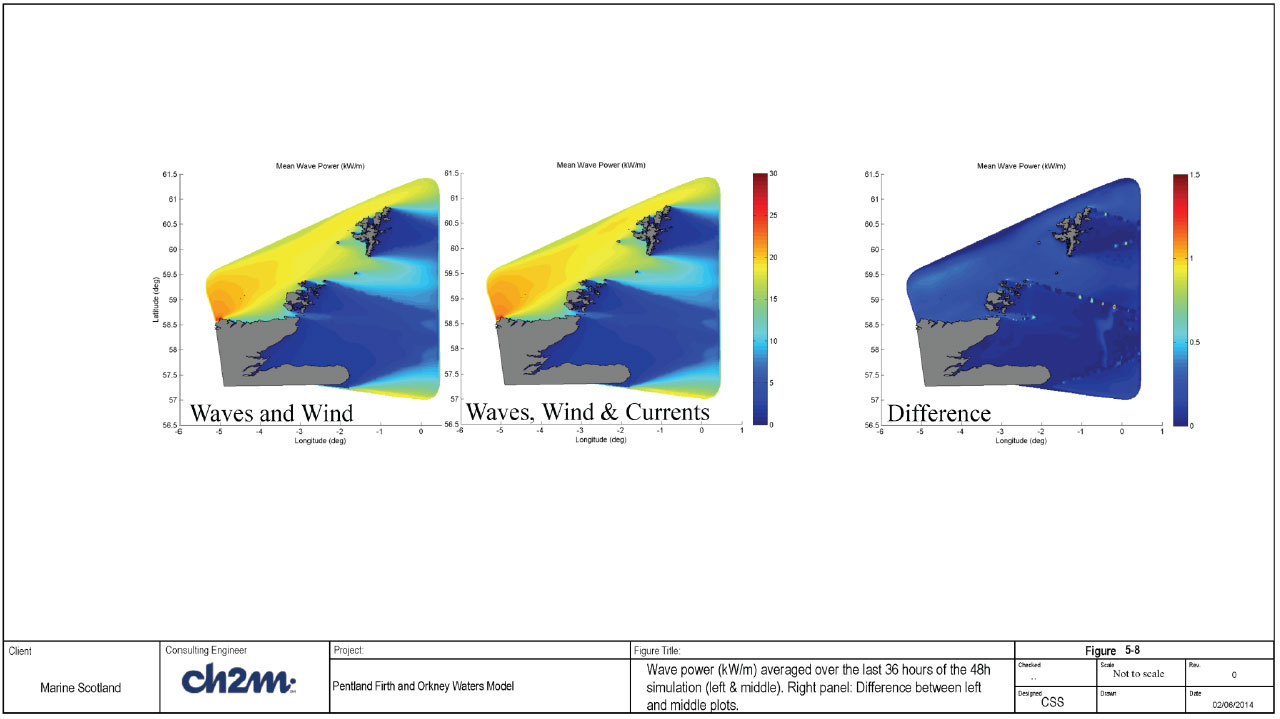
The detailed model results are shown in Appendix E (Figure E-26 to Figure E-30), while the key results are shown in Figure 5-7 and Figure 5-8. Figure E-26 shows that the tide is well predicted by the model (Figure E-26), while Figure E-27 show that the maximum currents in the area are attained in the Pentland Firth. The main result from the investigation is that the effect of wave current interaction on the wave parameters is small (< 0.1m for wave height and 2 to 4 deg for wave direction). Similarly, the effect on wave power is small, but localised changes of up to 10% in wave power was found at a few locations. Furthermore, the effect of increased turbulent mixing due to surface waves is not noticeable in the calculated depth-averaged current speeds or water levels. However, the absence of any noticeable effect may be due to the limited number of vertical sigma-levels used in this assessment.
Other investigators have also reported that the effect of wave-current interaction on the calculated wave energy resource is small. For example, Hashemi et al (2014) carried out a study to investigate the impact of wave-current interaction on the NW European shelf seas. They carried out model simulations for January 2005 using a decoupled SWAN model, a one-way coupled model (in which calculated water levels and currents from a separate model are introduced into SWAN) and a fully coupled wave-current model using a model called COAWST. They concluded that the decoupled SWAN model, one-way coupled model, and the COAWST model seem to produce very similar results. However, they also observed that the impact in some specific regions (e.g. Orkney) can reach 10% of the resource.
Wolf et al (2006) also investigated the influence of wave-current interaction in Liverpool bay. They carried out a wave model hindcast for 26 January - 7 February 2003, using the coupled POLCOMS- WAM model, forced by Met Office mesoscale model winds. They also obtained buoy and ADCP observations for the same period. They concluded that the general agreement between model and measurements is very good. However, they observed marked tidal modulations of the wave height especially, and to a lesser extent the wave period, that are not captured by the coupled model. They found only slight differences between the uncoupled and coupled model runs for Liverpool bay.
The conclusion from the present study is however different from ABPmer (2012) who also studied the impact of wave-current interaction on wave parameters and wave energy resources in the PFOWSA. The ABPmer (2012) study was carried out by determining the difference in wave conditions for a waves-only run, and a simulation using one-way coupling (pre-calculated ebb and flood pattern of mean spring tidal currents used as input to the wave model). They found that the effect of wave -current interaction is quite significant. ABPmer calculated that the changes in Hm0 for ebb and flood flow are well above 20% at a number of locations including the Pentland Firth. However, they also observed that the large changes are mostly in areas where the baseline wave conditions is typically low. It is also important to note that they found little impact of wave-current interaction in the western part of the Orkneys where the wave energy resource is high.
In summary, the assessment of wave-current interaction on wave energy resources carried out in this study shows that the effect is generally small, but localised changes of up to 10% in wave power can be seen at some locations.
5.4 Approaches for assessing impacts of extracting energy
The energy available from currents and waves throughout the PFOW area without any energy extracting devices have been determined in the preceding sections. However the future use of the hydrodynamic and wave models will entail the determination of the impact from the extraction of tidal and wave energy from the system. If the flow or wave extracting device can be represented adequately in the numerical models, the impact of the device can be determined by post-processing of the model results to determine differences with the baseline conditions for a range of parameters. Thus, in this section, we focus on how the devices can be incorporated within the FVCOM model so that the impact of extraction of energy can be assessed.
5.4.1 Representation of flow energy devices in FVCOM
The ongoing Terawatt Project produced a report by Baston, Waldman and Side (2014) entitled "Modelling energy extraction in tidal flows". This position paper presents approaches used by a range of organisations and numerical models, to simulate the energy removed by energy extraction devices and the effect upon the surrounding hydrodynamics. The information contained within the Terawatt position paper should be read with this report, as the Terawatt project is an ongoing project which extends beyond the duration of the present study. This paper also goes into much more detail than can be included in this section of this report.
5.4.1.1 Scale of representation
Simulating the accurate shape and dynamics of a tidal energy device and its effect upon the immediate surrounding water body could only be simulated accurately using Computational Fluid Dynamic ( CFD) models. These are costly in terms of time and would only allow the structure to be simulated and not the wider regional area surrounding it which is usually the reason to simulate the devices. This is the reason why representation of tidal energy devices, assumed here to be turbines, are often represented as supra or sub-grid scale devices using 2D or 3D hydrodynamic models. Supra scale meaning that each device is resolved in one or more model elements (but not in the detail that a CFD model could do) whereas the sub-grid scale means that a device or number of devices are included within a model element that is larger than the device(s).
A tidal energy device will generally consist of rotating blades as well as a mounting structure (if mounted onto the bed) both of which can have an effect upon the water flowing past. There are the drag forces from the whole structure as well as the lift/rotational forces from the turbine blades which extract the energy from the water flowing by. Additional turbulence is also created from the structure and the revolving blades which can cause further mixing in the water column. The additional mixing may not be important for 2D model, but could be for a 3D model if the vertical structure is important.
Another factor to consider is the interaction between multiple devices deployed in an array. Representing a number of devices within one grid element, may allow for the representation of the effects from the drag and the energy extraction, but will not be able to simulate the hydrodynamic interaction between the structures. For example an acceleration of water may occur between two closely located devices creating faster flowing water downstream, likewise a shadow zone of slower, more turbulent water is likely to extend downstream of a turbine, which in turn could affect a turbine downstream.
In the current PFOW model the model elements within the Pentland Firth have, in general, dimensions of the order of 100m or more. It would be possible to refine the model mesh further around an array of devices in order to resolve the overall dimensions of each individual device, however this will have an impact upon the timestep used and would slow the model down.
The alternative approach is to use a subgrid scale representation. In this approach the energy extraction and drag forces for each device are parameterised within an element that is larger than the device itself, in fact this representation may include more than one device although the hydrodynamic interaction is then affected.
What would be preferable would be a mixture of both approaches with one device per model element, thus the resolution of the model is driven by the distance apart of the devices rather than the device size itself. This approach would then be able to include to some extent, the hydrodynamic interaction between the devices. If devices are close together however, then this approach may prove too costly in terms of increases to simulation time.
5.4.2.1 Representation of energy extraction
In 2D models, a structure such as a turbine and the support is often represented by considering the drag/lift forces as an increase in the local bed roughness, such structures are often parametrised as a pier. This allows for sub-grid scale structures to be represented by models with resolutions greater than the dimension of the structure itself. However as the turbine and structure will affect the flow in only part of the water column then the 2D approach is not entirely valid as the assumed model velocity profile will not be correct following the inclusion of the device.
Models such as MIKE3 can include structures by including the drag, and for turbines the lift forces also.
An alternative approach has been presented, Yang et. al. (2013) where a momentum sink was included in the underlying model equations (using FVCOM) to take into account drag of the supporting structure and the turbine blades, as well as the thrust from the turbine blades. This approach seems a sensible approach requiring a number of parameters to define the coefficients of drag and thrust. As given in Yang et. al. (2013), the momentum sink rate due to tidal energy extraction by tidal turbines can be defined generally as:-
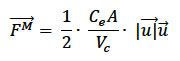
Where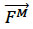 
is the momentum sink rate from a control volume, 
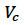by tidal turbines
C e is the momentum extraction coefficient
A is the flow facing area of the turbines, or turbine swept area
and,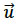 
is the velocity vector.
Yang, et al., goes on to further break down the momentum sink rate by subdividing a tidal turbine unit into three energy dissipative parts:-
1) turbine blades
2) turbine supporting poles
3) turbine foundation
Giving:-
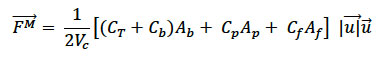
Where
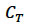is the turbine thrust coefficient for the amount of thrust exerted on a fluid, 
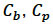, and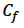 
are drag coefficients due to the physical structure of turbine blades, supporting poles and foundation. The area 
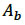is the flow-facing area swept by the turbine, 
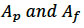are the total flow-facing areas of the supporting poles and foundation respectively. This general approach has also been implemented (with small changes) by Rory O'Hara-Murray of MSS (personal communication and presentation at UK FVCOM user group meeting).
5.4.2 Representation of wave energy devices in FVCOM
As part of the ongoing TeraWatt project, MacIver et al (2013) produced a comprehensive position paper that summarise various approaches of representing wave energy extraction in regional scale numerical models. They considered spectral wave models and Boussinesq wave models as best suited for regional scale hydrodynamic models considering the environmental impact of arrays of wave energy converters, where domains can extend up to several tens of kilometres. Potential flow or CFD models were considered more appropriate in the immediate vicinity of devices.
FVCOM wave model ( FVCOM- SWAVE) is a spectral wave model. The approaches for representing the devices in spectral models presented in MacIver et al (2013) are discussed below in relation to FVCOM.
The representation of wave energy converters in spectral models, either individually or as an array, can be achieved only through accounting for their influence on the wave energy density spectrum . Specifically phase-dependent effects cannot be accounted for directly, although certain effects, e.g. diffraction, can be modelled approximately. Furthermore, spectral wave models do not account for the scattering or radiating of energy by the wave energy converters.
Diffraction of wave energy is represented in spectral wave models (including FVCOM- SWAVE) using an approximate phase-decoupled refraction-diffraction formulation. Thus, the effects are not well reproduced in the immediate vicinity of a structure (i.e. within a few wavelengths). The diffraction option can be switched on in the INPUT file for FVCOM- SWAVE. However, this option has not been tested in this project.
5.4.2.1 Supra-Grid representation
In the supra-grid representation, each individual device within the array is resolved in the model, and a sufficient number of cells (at least 5 cells) are used to resolve the spaces within the individual devices. An explicit frequency dependent transmission coefficient is specified at each device (Foley et al, 2012). This ensures that the model can represent the effect of wave energy extraction for different frequencies at each device.
It is possible to resolve individual devices in the FVCOM SWAVE model (at mesh generation stage), hence this method can be used in principle. However, there is presently no facility to specify a frequency dependent transmission coefficient in FVCOM. The only alternative is to model the devices as small islands, with the surface of each island taken as an absorbing layer. This will however not model the wave energy extraction at the devices correctly.
5.4.2.2 Subgrid representation
In the subgrid representation, the energy absorption characteristics of individual device is represented as a point source [or sink] of energy at a computational node by including an additional frequency and directionally dependent source term (S wec) in the governing equation (Silverthorne & Folley 2011, Weywada, Child & Cruz 2012, Greenwood, Christie & Venugopal 2013).
S wec = c g C(f,) E(f,)
where c g is wave group velocity, C(f,) is a frequency and directionally dependent coefficient for the wave energy device.
The source term, S wec is not implemented yet in FVCOM. Hence, it is presently not possible to use this method in FVCOM without significant additional coding.
Contact
There is a problem
Thanks for your feedback