The Scottish Shelf Model. Part 2: Pentland Firth and Orkney Waters Sub-Domain

4 Wave Model Development

4.1 Introduction

The objective of the wave modelling study is to construct a calibrated and validated wave model for the Pentland Firth and Orkney Waters ( PFOW) using the fully spectral wave model, FVCOM- SWAVE. Furthermore, the wave model is used to carry out one-year long simulation for mapping available wave energy resources in the PFOW model area.

Originally, the one year simulation was to be carried out using idealised forcing. After discussions with Marine Scotland ( MS), it was agreed that the one-year simulation be carried out for the year that best represents the average year from the available dataset. This year is referred to as the representative year.

The remainder of this section of the report is organised as follows. A description of the wave model setup is given in Section 4.2, followed by the wave model calibration in Section 4.3. The analyses carried out to determine the representative year is presented in Section 4.4 together with key simulation results from one-year simulation. Lastly, the conclusions from this study are presented in Section 4.5.

4.2 PFOW wave model setup

FVCOM- SWAVE is an unstructured-grid finite-volume spectral wave model, developed by implementing finite-volume algorithms within SWAN (Qi et al, 2009).

SWAN (Simulating WAves Nearshore) is the third-generation spectral wave model developed originally by Booij et al. (1999) and improved through a team effort ( SWAN Team, 2006a). The model solves the wave action balance equation and takes into account the effects of refraction and shoaling due to varying depth, diffraction, local wind-wave generation, nonlinear wave-wave interaction, wave-current interaction and energy dissipation due to bottom friction and wave breaking. The model is used to simulate local wind-wave generation and the transformation of offshore waves into shallow waters.

Since FVCOM- SWAVE is an unstructured grid implementation of SWAN, it includes all the key processes included in SWAN, with the added flexibility of using an unstructured grid (mesh). This provides the user the flexibility to use coarser meshes away from the area of interest and gradually increase the mesh resolution towards the coastline or specific areas of interest.

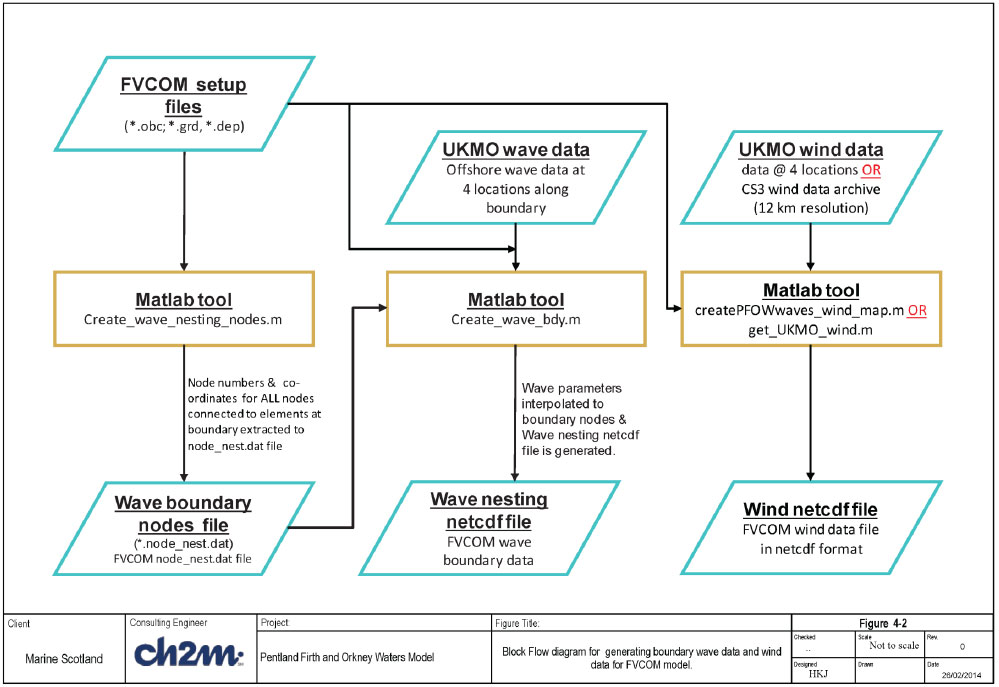
Schematic block flow diagram for preparing the required model setup files are shown in Figure 4-1 and 4-2. The steps in these figures are discussed in the sub-sections below.

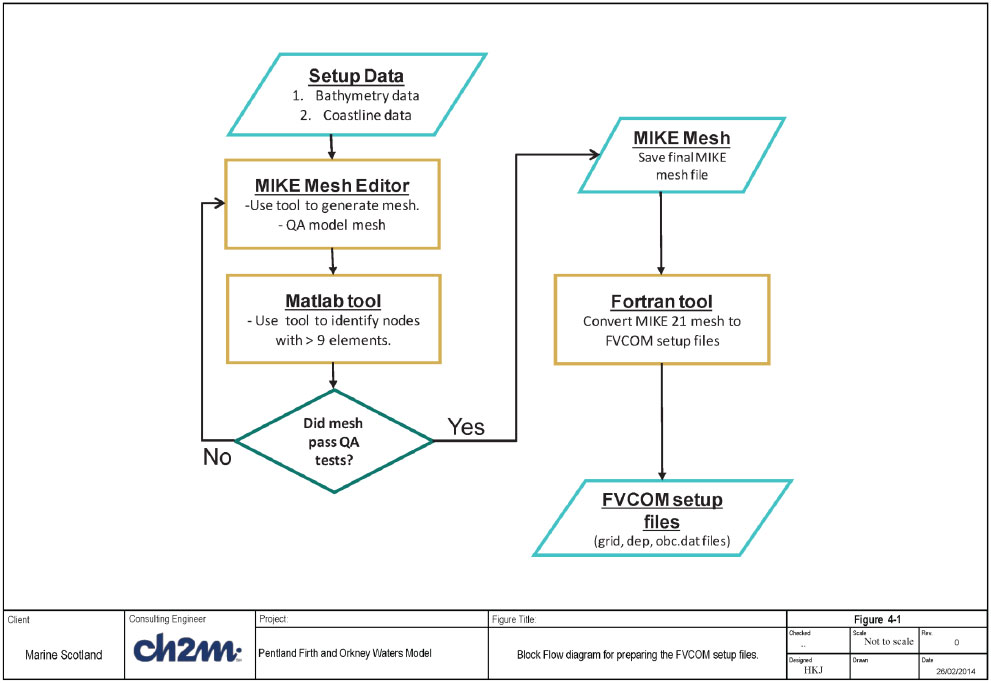
4.2.1 Model mesh

The model area covered by the wave model is identical to the model area covered by the hydrodynamic model (discussed in Section 3). The initial consideration was to use the same mesh as that developed for the hydrodynamic model for the wave modelling task. However, initial tests showed that this leads to unrealistic computational times using the available IT resources (Dell R815 with 64 processor cores). For an illustration, the hydrodynamic model mesh (at the time of evaluation) has 85,840 nodes (161,141 cells). With the wave energy spectrum divided into 25 discrete frequencies and 24 discrete directions, the wave model simulation (excluding any coupled wave-current interaction) is estimated to take 13 hours for every 24 hr simulation period (using 30 cores on the Dell R815). This is considered unrealistic, and a new model mesh was constructed for the wave model.

The wave model mesh has been created using DHI's MIKE 21 mesh generator tool (described in Section 3.2.1). The horizontal coordinate system used is latitude and longitude with a vertical datum of mean sea level.

The bathymetry and coastline data used are the same as described in Section 3.2.1. These data are loaded into the mesh generator tool (Figure 4-1) and the tool used to generate triangular meshes throughout the model area. The mesh resolution in different areas have been varied by specifying maximum element area sizes in various polygons, see Figure 4-3. In order to improve the computational time for the wave model, the following modifications were made in generating the mesh:

• All islands in the open sea with length scale < 1km are deleted. These islands usually require high resolution to resolve the island boundary, and this forces the mesh to have very dense meshes in the immediate vicinity of the island.
• The resolution used to describe the boundary of the polygons and the coastlines were modified as shown in Table 4-1.

The indicative mesh sizes for the different polygons are shown in Table 4-1. The highest resolution is in the Pentland Firth and Orkney waters, where the resolution is typically about 250m to 500m.

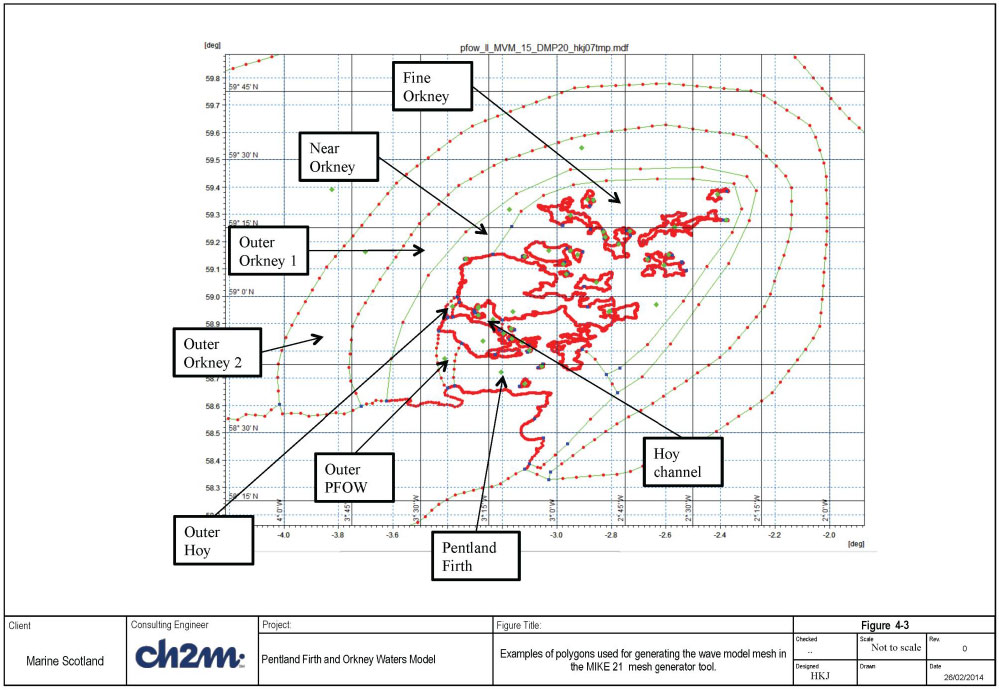
Table 4-1 Mesh resolution in the FVCOM- SWAVE model for PFOW.

Polygon	Resolution (deg) along polygon / shoreline	Max element area (deg 2)	Indicative resolution (km)
Outer	0.1 / 0.050	20E-04	5.00
Shetland	0.1 / 0.050	15E-04	4.00
Orkney 2	0.1 / 0.035	10E-04	3.50
Orkney 1	0.1 / 0.020	5.0E-04	2.00
Near Orkney	0.1 / 0.010	2.5E-04	1.00
Fine Orkney	0.1 / 0.005	1.2E-04	0.50
Outer Hoy	0.1 / 0.005	1.2E-04	0.50
Hoy channel	0.1 / 0.005	0.8E-04	0.50
Outer PFOW	0.1 / 0.005	0.8E-04	0.50
PF	0.1 / 0.005	0.5E-04	0.25

The process for generating the mesh is an iterative process as schematised in Figure 4-1. The iterative process is used to ensure that the model mesh complies with the FVCOM- SWAVE model mesh requirements. These are:

• The number of elements connected to any mesh node should not exceed 8.
• The areas of the mesh should vary smoothly (not more than a factor of 2 to 3) throughout the model area.
• The mesh triangles should not have angles that are too acute (less than 30 ^o).

Experience has shown that the model is especially sensitive to violation of the first two constraints, as this typically results in early development of model instabilities or the model not running. The PFOW wave model mesh is shown in Figure 4-4.

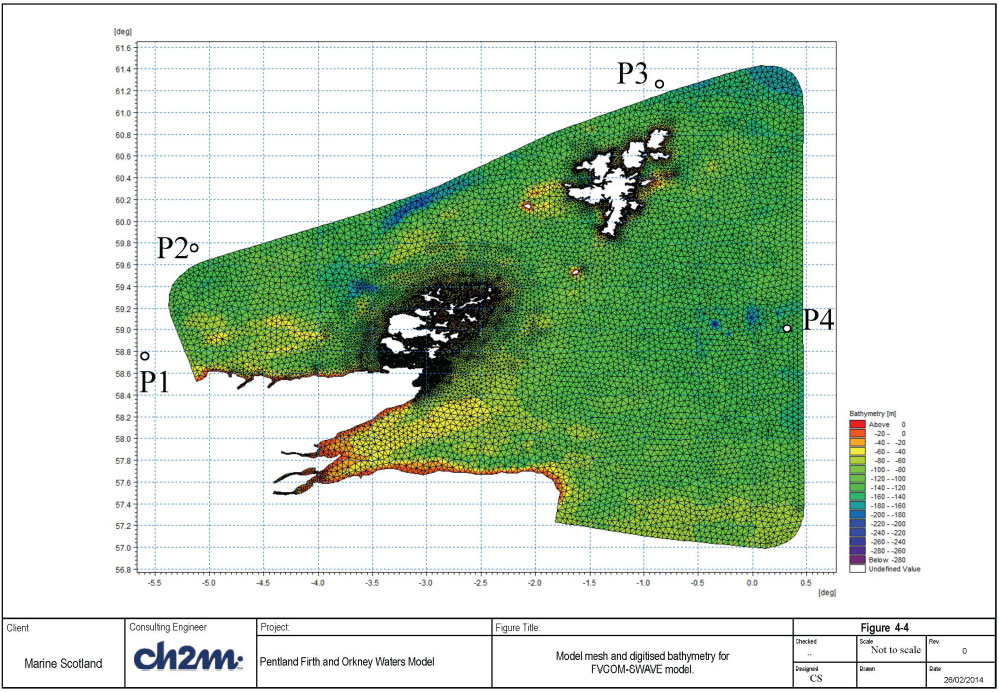
4.2.2 Model bathymetry

The bathymetry data used for the wave model is the same as used for the hydrodynamic model (see Section 3.2.2). The bathymetry data consists of the following datasets in order of priority: a) UKHO (United Kingdom Hydrographic Office) and Marine Scotland datasets; b) EMODnet/ NOOS datasets; and c) digitised bathymetry data from Admiralty Charts. Further details are given in Section 3.2.2.

The bathymetry data was interpolated onto the model mesh to create the digitised model bathymetry. The digitised model bathymetry is shown in Figure 4-4. The mesh file produced by the MIKE 21 tool includes information about the mesh (node co-ordinates and element connectivity), bathymetry (depths at all nodes) and special markers for open boundary nodes. This file is used as input file to a FORTRAN tool that generates the required FVCOM setup files for describing the mesh (grid file), the bathymetry (dep file) and the nodes along the open boundary (obc file).

4.2.3 Boundary wave data

Wave data are obtained from the UK Met office ( UKMO) under a licence agreement with Marine Scotland, at locations P1 to P4 (see Figure 4-4). The wave data cover a 13-year period, from January 2000 until December 2012. The data is from three UKMO wave hindcast models, namely: a) European model for the period 01/2000 - 03/2000; b) UK Waters model for 03/2000 - 11/2008; and c) WaveWatch III (WW III) model for 1/2008 - 12/2012.

The wave data is in the form of 3-hourly time series of wave parameters (wave height, period and direction) for swell component, wind-wave component and the resultant (combined swell and wind-waves). The model was forced using the resultant wave parameters. The two dimensional energy spectrum was specified by imposing JONSWAP frequency spectrum (peakedness parameter, Gamma =3.3) and cos^5 directional distribution function.

The wave data at P1 to P4 are interpolated along the boundary of the wave model ( note that the wave parameters should be interpolated to all nodes connected to elements located along the model boundary) to create an FVCOM wave nesting file. This file is used to specify the wave conditions along the boundary of the model. A block flow chart illustrating how the wave boundary data file is derived is shown in Figure 4-2.

4.2.4 Wind data

Two sources of wind data were available for this study. These are:

• Wind data (hourly averaged wind speed and direction) provided by UKMO at locations P1 to P4. The wind data cover the same period as the wave data and are available as 3-hourly time series data. This dataset is hereafter called 4-pt wind data.
• Hourly wind fields from the UKMO ( UK Met Office) forecast models that have been archived at NOC-L. This dataset have been presented in Section 2.3.2.1. The relevant dataset for the wave study is the post-1995 surface wind data, which is available at 12km resolution. This dataset is hereafter called the 12km wind data.

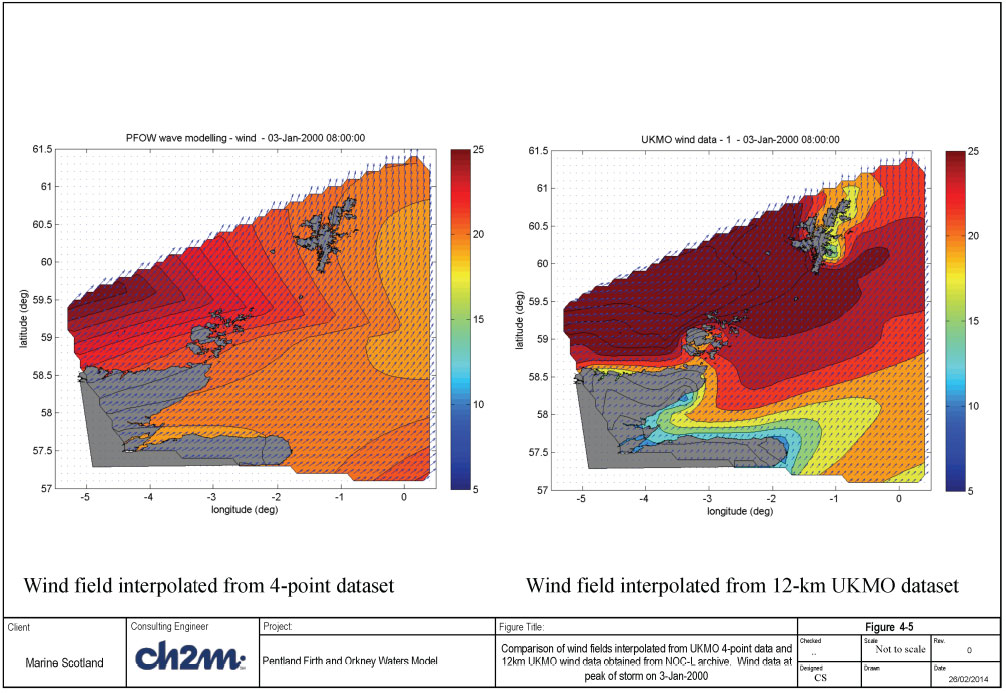
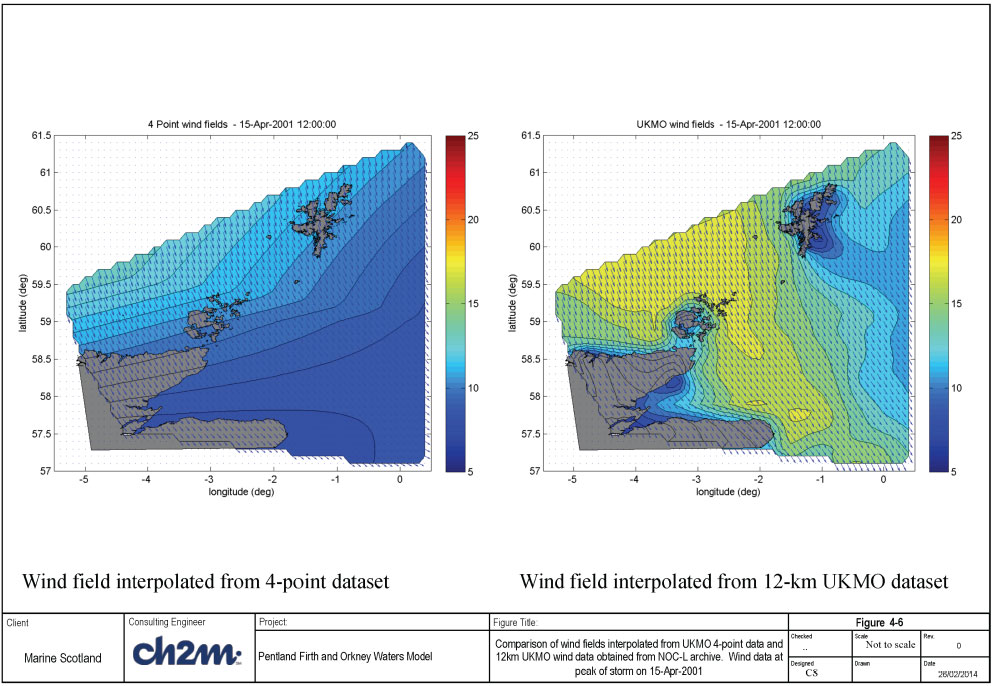
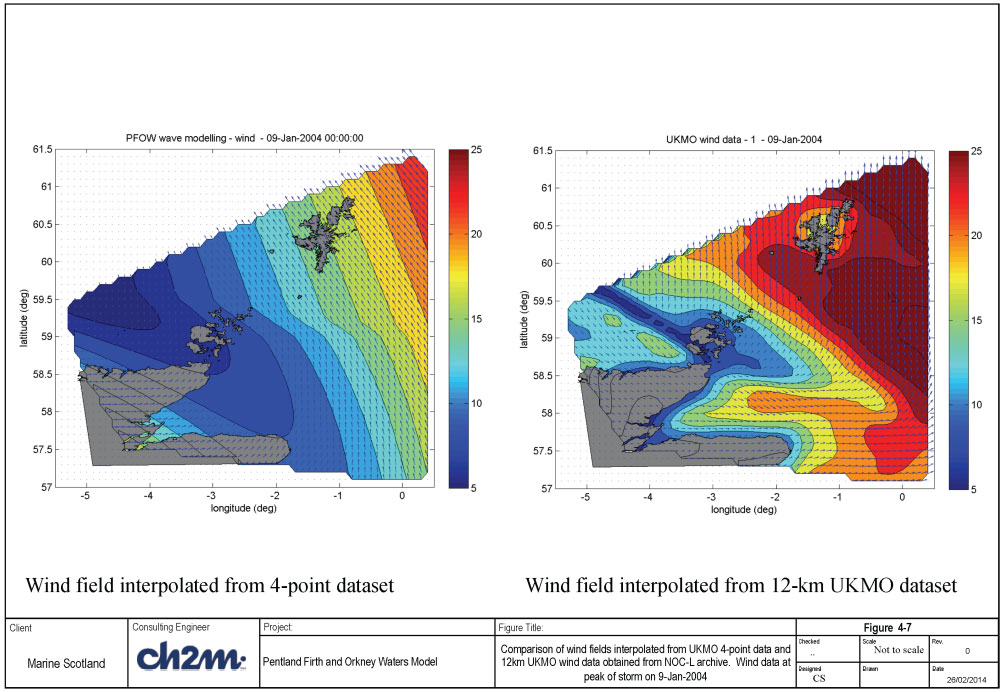
In order to use these data for the wave simulation, the wind data for the selected simulation periods are interpolated onto the FVCOM grid using Matlab scripts (see Figure 4-2). Example comparisons of the interpolated wind fields using the 4-pt wind data and the 12km wind data are shown in Figure 4-5 (peak of storm on 3-Jan-2000), Figure 4-6 (peak of storm on 11-Apr-2001), and Figure 4-7 (peak of storm on 9-Jan-2004). These figures show that the broad features of the wind fields are reproduced in the 4-point data; however, the 4-point data omit a number of details that are seen in the 12km wind data.

4.3 Wave Model calibration

Model calibration is a procedure where the following tasks are undertaken:

• Numerical model is run with selected model parameters
• Model results are compared with measurements (in the area of interest) to check if the agreement between the model results and measurements is acceptable. Relevant model parameters are adjusted and the model re-run.
• The preceding step is repeated until acceptable agreement between the model results and measurements is achieved. When this is achieved, the model is considered to be calibrated.

In order to carry out model calibration, the following information is required: a) measured wave data, and b) target quality measure/s for quantifying and accepting the level of agreement between model results and measurements.

4.3.1 Wave calibration data

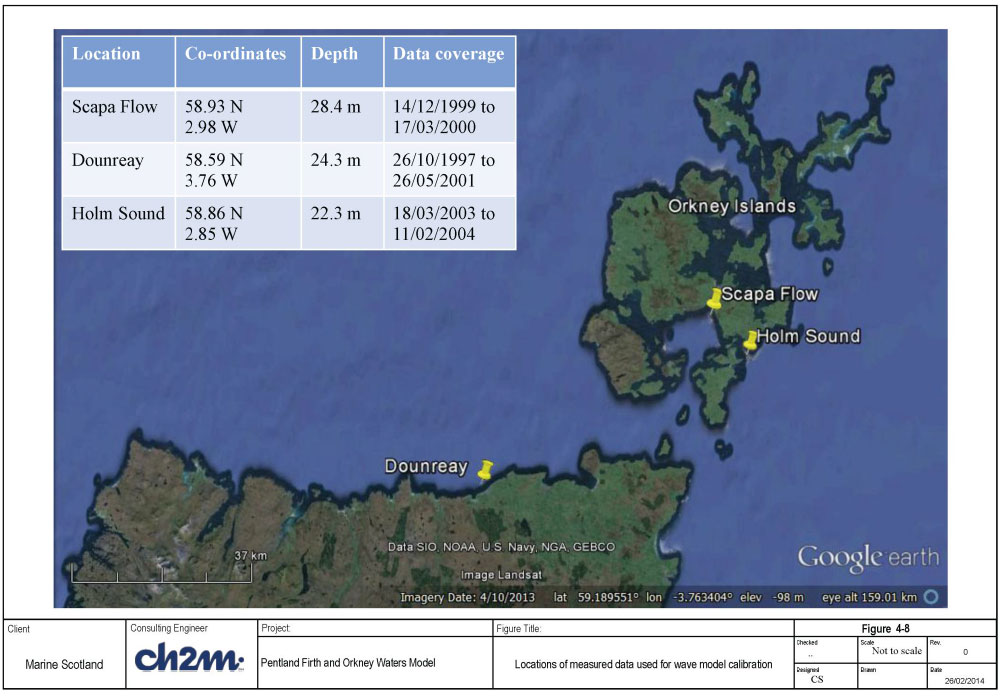
Measured wave data that can be used as calibration data are available at the three locations shown in Figure 4-8 and Table 4-2.

Table 4-2 Calibration data used for wave modelling

Location	Co-ordinates	Water depth (m)	Data coverage
Scapa Flow	58.93 N, 2.98 W	28.4 m	14/12/1999 to 17/03/2000
Dounreay	58.59 N, 3.76 W	24.3 m	26/10/1997 to 26/05/2001
Holm Sound	58.86 N, 2.85 W	22.3 m	18/03/2003 to 11/02/2004

4.3.2 Wave calibration targets

In a publication by ECMWF, ("The Wave Model", http://www.ecmwf.int/en/learning/education-material/lecture-notes, slide 114), the modelled wave data was compared with buoy measurements for the period February to April 2002. The root mean square error ( RMS error) for wave height was calculated as 0.44m, and the corresponding scatter index ( SI = RMS error/mean of the measured data) is about 18%. The RMS error for peak wave period was 1.75s and the SI was 19%.

Lawrence et al (2009) carried out calibration of the MIKE 21 SW wave model at a location near the Orkney Islands. They described agreement between the modelled and measured wave height with a SI of 12% as "exceptionally good results" using improved wind forcing. The OWI wind forcing that was initially used gives SI of 18% for November 2005. This is still considered good. No quality metric was provided about the agreement with wave period or wave direction. Based on experience at Halcrow, the agreement between measured and modelled wave height is usually considered good if the RMS error is less than 0.3m or the scatter index is less than 20%. However, this is not always achievable depending on the accuracy of the best available boundary wave data and wind data. In such cases, the target is to get the best quality measure that can be realistically achieved.

4.3.4 Model parameters

The parameters used in the model simulations are summarised in Table 4-3.

Table 4-3 Wave model setup parameters

Parameter	Value
Software:	FVCOM v3.1.6 (latest FVCOM, released in August 2013).
Spatial grid:	PFwv07, spherical grid co-ordinates (lon/lat); 23,508 nodes; 41,666 cells
Frequency grid:	JONSWAP shape, f_low= 0.05; f_high = 0.5, No of frequencies = 24
Direction grid:	Cos^5 spreading, D_low= 0; D_high = 360, No of discrete directions =24
Forcings:	Boundary waves: Varies (depending on the simulation) Wind conditions: Varies (depending on the simulation)
Water level:	0.0m (i.e. MSL)
Model physics	Wind Generation: GEN=3, GROWTH=KOM/JANS, AGROW=F Bottom Friction: Jonswap formulation, Cfjon=0.067 Whitecapping: WCAP= varies (Komen & Janssen - KOM/JANS) Wave breaking: alpha=1, gamma=0.73 (Battjes & Janssen) Wave-wave interaction: Quadruplet wave interaction
Time steps:	Flow part: OFF in Waves ONLY run, but should be specified External timestep = 1s; ISPLIT= 6 Waves part: Propagation: NS_DELTC = 12.0s Source terms: DTMIN = 1.0, DTMAX = 12.0s
Others:	Minimum water depth = 1.0m Nautical=True PWTAIL=4 (Non-diagnostic high frequency tail)

The following parameters are used as calibration parameters:

1. Wind-wave generation source term.
This term controls the rate at wind adds energy to the growing waves in the model. It is particularly important in areas where waves are dominated by locally generated wind waves. Different formulations are available for this term in FVCOM- SWAVE. For this study, we have investigated: 1) Janssen formulation and 2) Komen formulation.

2. Whitecapping source term.
This term controls the rate at which energy is dissipated in the waves due to whitecapping (waves becoming too steep leading to wave breaking and whitecapping). Different formulations are available for this term in FVCOM- SWAVE. For this study, we have investigated: 1) Janssen formulation and 2) Komen formulation.

3. Bottom friction.
This term controls the rate at which energy is dissipated in the waves due to the effect of bottom friction. This is mainly important in shallow and intermediate waters. It is not important in deep water as the waves do not feel the bottom. Different formulations are available for this term in FVCOM- SWAVE, and the effect can also be controlled by the bed roughness parameter (or bottom friction coefficient).

4. Wind data.
Various studies have shown that the adequacy of the wind data is one of the most important parameters for wave modelling. Two wind datasets are available for this study (4-point wind data and 12 km data). The latter is the most detailed wind information that is available.

4.3.5 Initial simulation runs

After completing the model setup, it was found that the model did not run (stopped with error messages) for the initial test runs. The following FVCOM files were modified in order to get the wave model to run using our installed version of Intel Fortran compiler:

• Mod_nctools.F
  This was modified to fix the error message: "CAN NOT UPDATE TIME FOR INVALID FLOATING POINT TIME VARIABLE."
  
  An alternative fix is to include:
  DATE_REFERENCE = 'default' in the namelist file
• Swanmain.F
  This was modified to fix error message in subroutine SWINCO: VARS_WAVE: Name in only list does not exist [M, MT, N, NGL, NPROCS, MYID].
  
  These variables are not defined explicitly in Module VARS_WAVE. However, they are defined in Module LIMS which is embedded in module ALL_VARS which is also used in this subroutine. The fix was to remove the 'offending' variables from VARS_WAVE, ONLY list.
• Mod_nesting.F
  For building the FVCOM code, the file mod_nesting.F in FVCOM v3.1.6 is replaced with a new version provided by Dr J. Qi (from Prof Chen's group) in Nov 2013. He mentioned that this is required to keep the unit of time as default modified Julian Day ( MJD).
• INPUT (specification file for SWAN):
  PWTAIL should be set to 4 or higher. Setting PWTAIL=3 triggers an error message: "error tail computation"

After making these modifications, a number of initial simulations were carried out using constant wind forcing. The key lessons learnt from these simulations are summarised below:

• FVCOM v3.1.6 model was found to be more stable than earlier versions of FVCOM (that included a wave model).
• As expected, the wind wave growth in the model is quite sensitive to the wind formulation used.
• The instability in the model is removed by using a wave propagation time step (NS_DELTC) determined using the Courant condition:
  • Cr = Cg _max*dt / dx ≤ 1
  • dt ≤ dx _min / Cg _max
  • Using f _min = 0.05, dx _min = 250m, dt ≤ 16s. In practice the time step used is lower than the maximum value.

4.3.6 Calibration runs

The wave model calibration runs were carried out for selected periods in January 2000, April 2001 and January 2004. The calibration was carried out using available wave measurements at Scapa Flow, Dounreay and Holm Sound.

The locations of the measurement data make it possible to investigate the adequacy of model description of a number of key physical processes in the study area, see Table 4-4.

Table 4-4 Characteristics of the locations with measured data

Location	Site Characteristics	Processes checked in the model
Scapa Flow	Sheltered from offshore waves approaching from the North, West or East.	Local wind-wave generation
Dounreay	Located at an exposed location on the western approaches to the Pentland Firth.	Offshore wave propagation towards the western section of the Pentland Firth.
Holm Sound	Located at an exposed location on the eastern side of the Orkneys.	Offshore wave propagation from the North Sea towards the eastern coast of the Orkneys and the Pentland Firth.

Measured wave data in the Pentland Firth would have been useful for investigating the effect of wave-current interaction in the firth, as the current speeds are quite high in this area. However, we are not aware of any dataset in this area.

4.3.6.1 Jan 2000 simulation - Scapa Flow

The following model runs are carried out for selected periods in January 2000:

• Run 1: No wind
• Run 1A: 4-point wind; Janssen wind input; Janssen whitecapping
• Run 1D: 4-point wind; Komen wind input; Komen whitecapping

The modelled wave height for the "No wind" case is less than 0.1m throughout the simulation. This is as expected, as this area is well sheltered from offshore waves.

The results with the 4-point wind data are generally similar, but the wave heights are slightly higher for the Komen formulation.

Initial simulations using the 12km wind were not successful (Run 1C, 1E, etc). It was found that the wind field (wind speed components) written into the wave output file is very different from the wind field in the input wind netcdf file. The problem was traced to errors in the matlab script used to prepare the wind netcdf file (a transpose error in the node connectivity variable written into the wind netcdf file plus a couple of additional errors in the file attributes). These errors were corrected and the 12km hourly wind field used for the calibration simulations. Table 4-5 provides a summary of investigations using the 12km wind field for calibration.

Table 4-5 Model runs with 12km wind fields.

Run ID	Description	Remarks
01J	Wind data - 12km UKMO wind Wind input - Komen formulation Whitecapping - Komen formulation	Calculated wave heights are too low in Scapa Flow (<0.3m throughout 01-Jan-2000). Conclusion: Setup not considered viable.
01K	Wind data - 12km UKMO wind Wind input - Janssen formulation Whitecapping - Janssen formulation	The calculated wave heights were improved compared to Run 01J. However, the wave heights were still underestimated. The underestimation was about 50% at the peak of the storm (measured peak Hm0=3.2m, simulated peak Hm0=2.0m). Conclusion: Results are promising, but there is a need to increase wind forcing in the model. Alternatively, the whitecapping dissipation may need to be reduced.
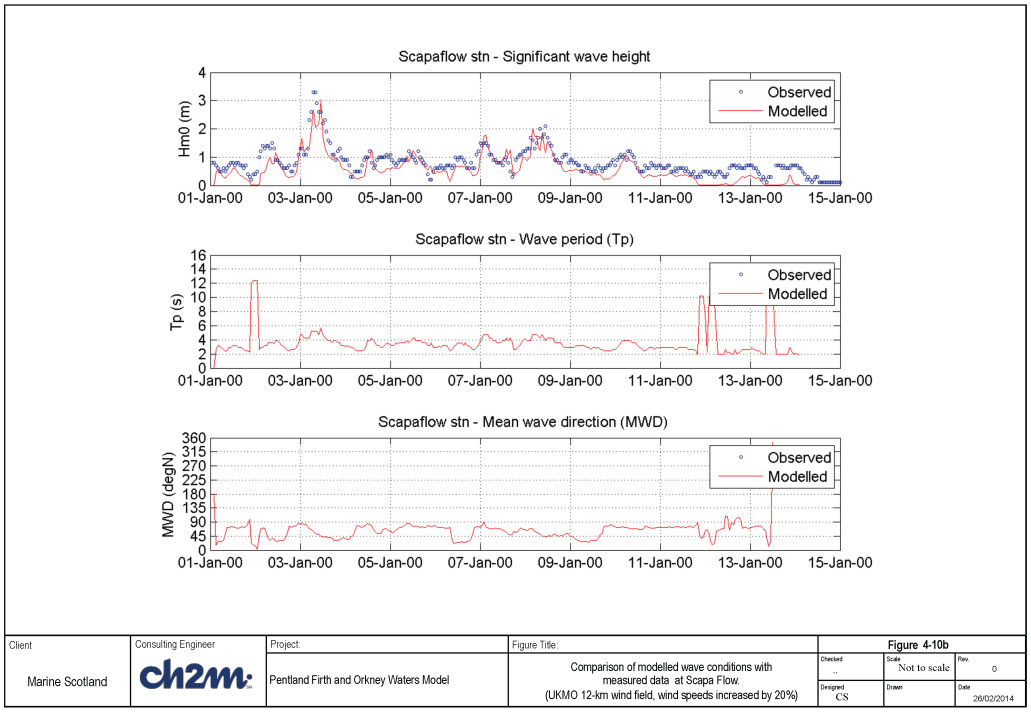
01L	Wind data - 12km UKMO wind scaled by 1.2 Wind input - Komen formulation Whitecapping - Komen formulation	The calculated wave heights were significantly improved compared to Run 01K, see Figure 4-10b. Conclusion: Setup considered to be adequate.

The final setup makes use of the 12-km UKMO wind speeds multiplied by 1.2. This multiplication factor was found to be necessary in order to get reasonable agreement between the measured and modelled wave conditions at Scapa Flow. We consider that this factor adjusts the UKMO wind data from hourly averaged wind data ( UKMO wind data is provided every hour) to wind data averaged over a shorter duration required in the numerical wave model (averaged duration that is consistent with the time step used in the integration of the wind-wave growth source terms). For example, Brown et al (2013) investigated the influence of wind variability at sub-hourly time scales in a numerical model and concluded that the inclusion of wind variability can lead to a difference in wave height of up to 35% compared to the use of 3-hourly wind data. This clearly suggest that if 3-hourly wind data is used, this should be multiplied by a factor (>1) in order to reproduce the correct wave heights. Resio and Westerink (2008) noted that ocean wave models use winds averaged over 10 to 30min, while CEM (2006, Part II, Chapter 2) suggests that the required wind averaging interval can vary depending on the size of the water body (1 to 5mins for small ponds, and 15 to 30mins for large lakes or oceans). For this study, the multiplication factor of 1.2 has been determined from calibration.

A summary of the calibration quality measures for selected runs is shown in Table 4-6. Only measured wave heights are available at Scapa Flow, hence no calibration measures are available for peak wave period and mean wave direction. Table 4-6 shows a very high negative bias for Run 1 (No wind). This is as expected, since the wave heights at Scapa Flow are dominated by the local wind. This is significantly improved by applying wind forcing to the simulation.

Table 4-6 Model quality measures at Scapa flow for 01 Jan - 14 Jan 2000 simulation.

Simulation Quality indices	Run 1 No wind	Run 1A 4-point wind + Janssen wi + Janssen wc	Run 1D 4-point wind + Komen wi + Komen wc	Run 1L Scaled 12km wind + Janssen wi + Janssen wc
Hm0: Mean error, bias (m)	-0.80	-0.18	0.12	-0.26
Hm0: RMS error (m)	0.92	0.37	0.32	0.35
Hm0: SI ( RMS/mean Hm0)	1.15	0.45	0.38	0.41
Hm0: Correlation coeff.	-1.0	0.78	0.77	0.87

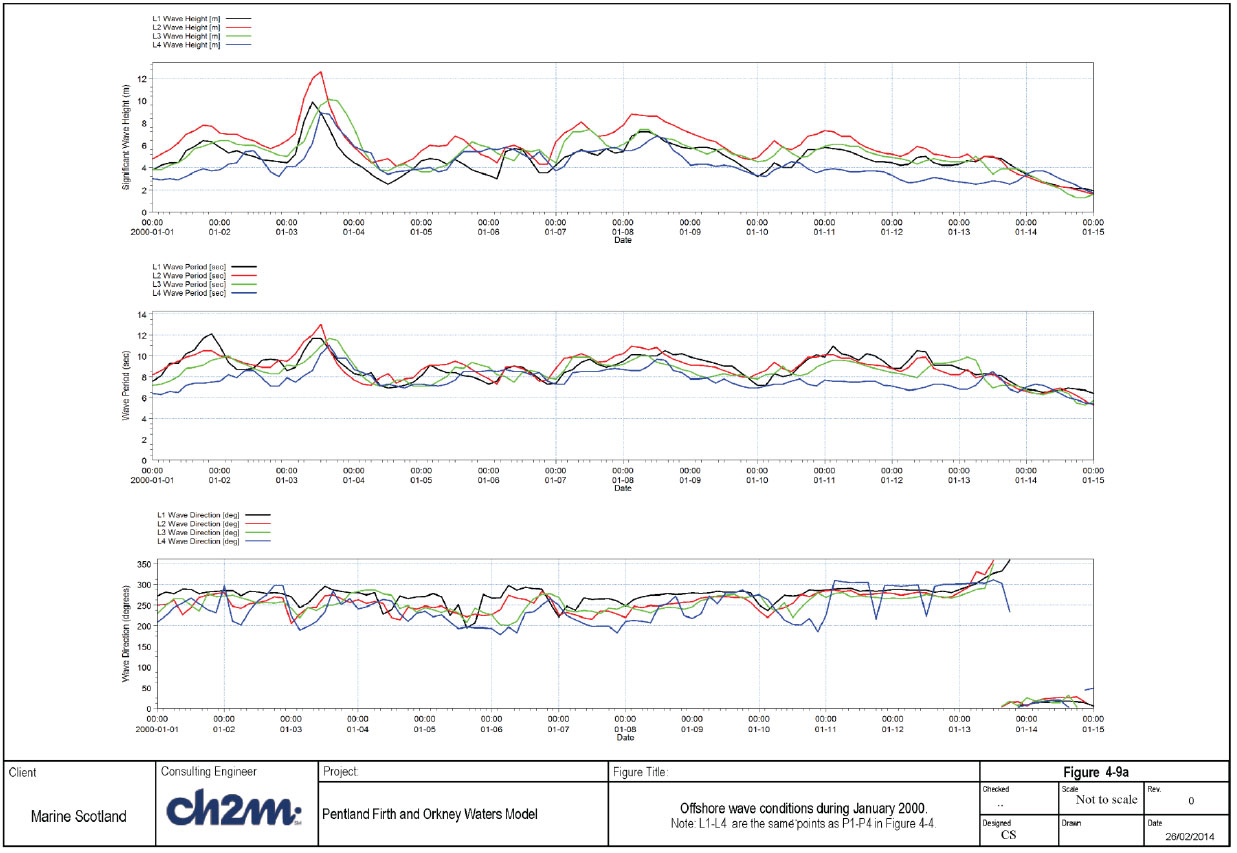
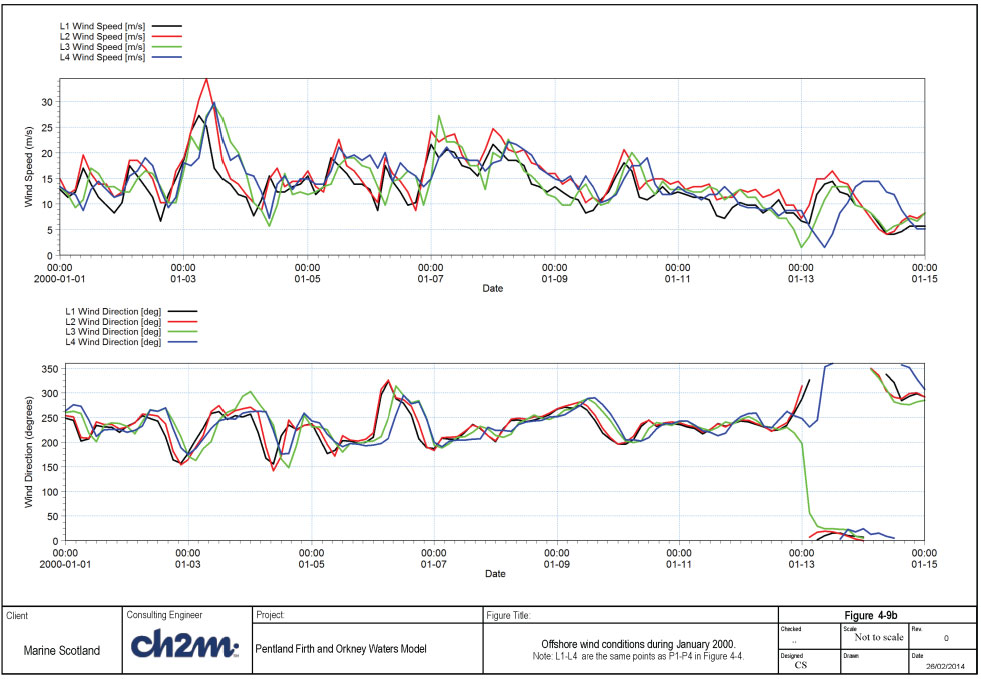
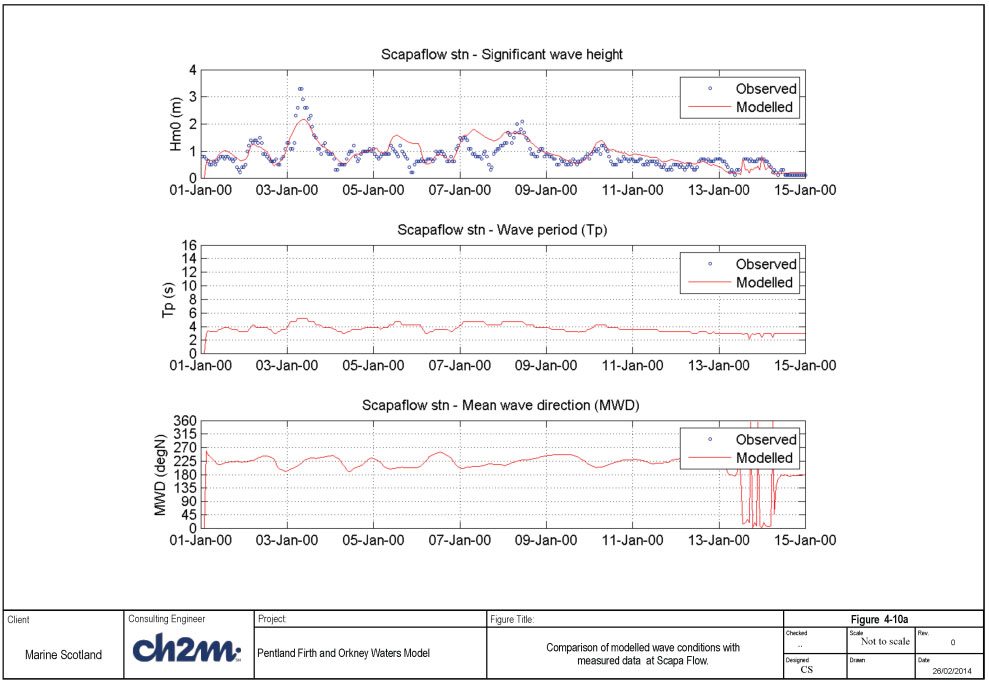
Time series of wave conditions during the simulated period at the 4 UKMO points are shown Figure 4-9a, while the time series of wind conditions are shown in Figure 4-9b. The modelled and measured wave conditions are shown in Figure 4-10a for the model setup with the smallest scatter index (Run 1D), and Figure 4-10b for the model setup with the highest correlation coefficient (Run 1L).

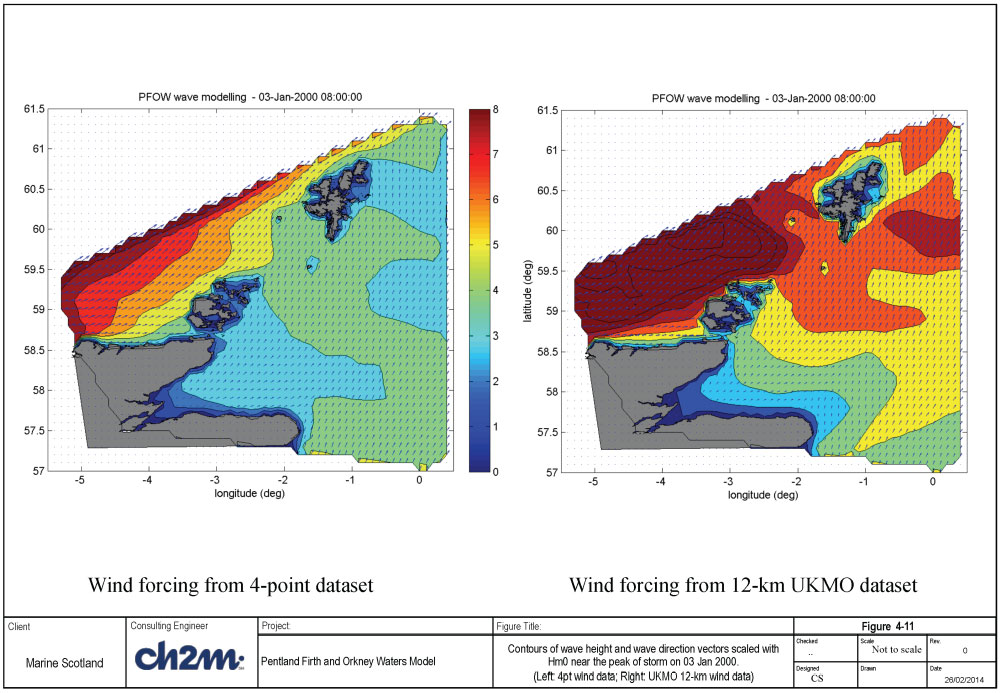
The largest storm during the simulation period occurred on 03 January, with offshore significant wave height of 9 to 12m, from SW to WNW sector. The corresponding maximum winds vary from 25 to 35m/s at the four locations. The observed peak wave height during the storm is about 3.3m, while the modelled peak wave height is under-estimated (just over 2.0m) for the 4-point wind data (Run 1D). On the other hand, the simulation with the 12-km wind (Run 1L) provides better agreement (peak wave height of about 3m) with the measurements (see Figure 4-10b). Overall, Run 1L is considered to provide the best agreement between the measured and predicted wave heights.

Figure 4-11 shows two-dimensional contours of significant wave heights and wave direction pattern (scaled with wave height) at the peak of the storm. The left panel shows the best result using the 4-point wind data, while the right panel shows the best result using the 12-km wind data.

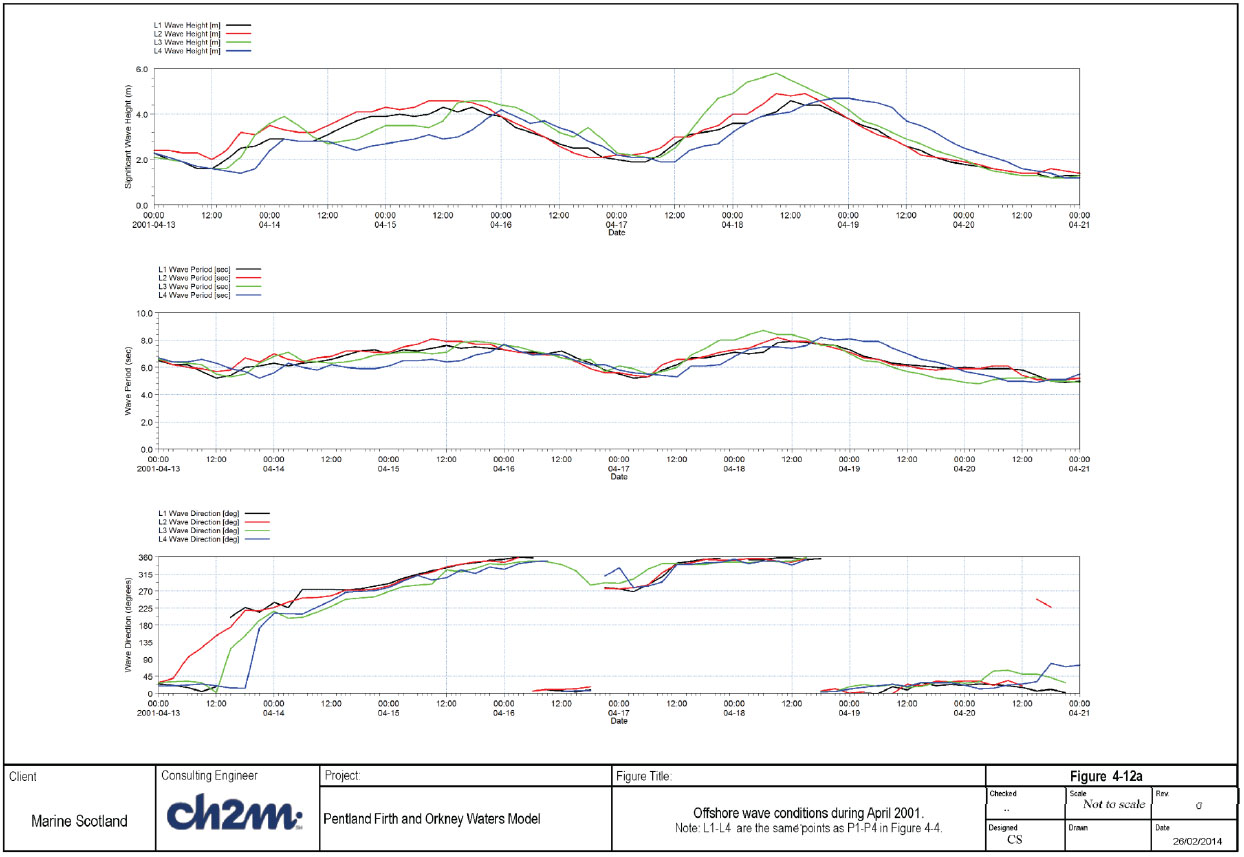
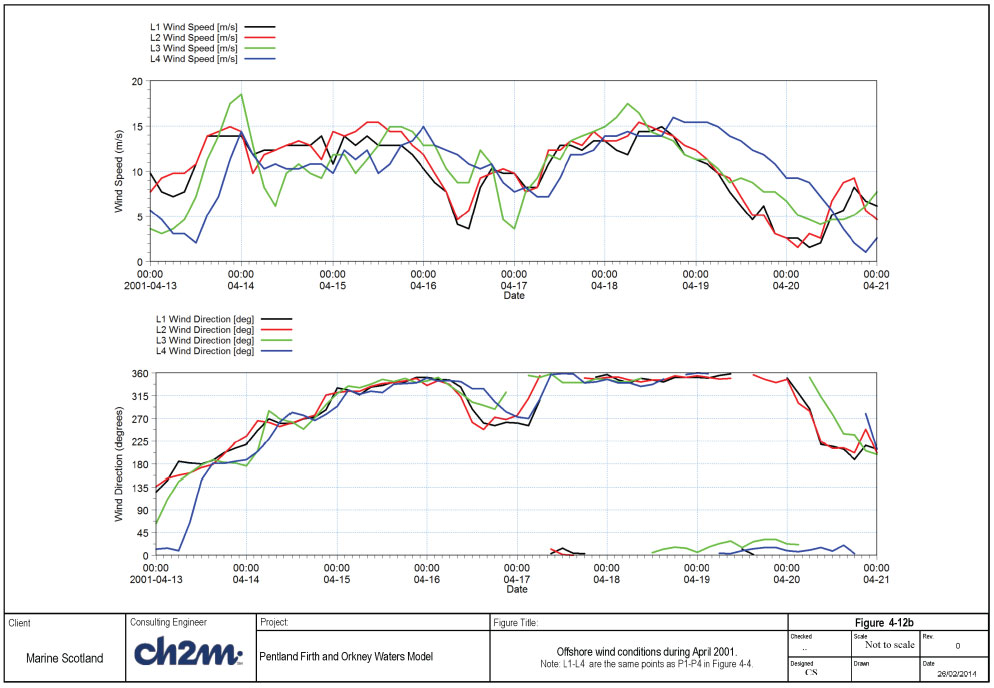
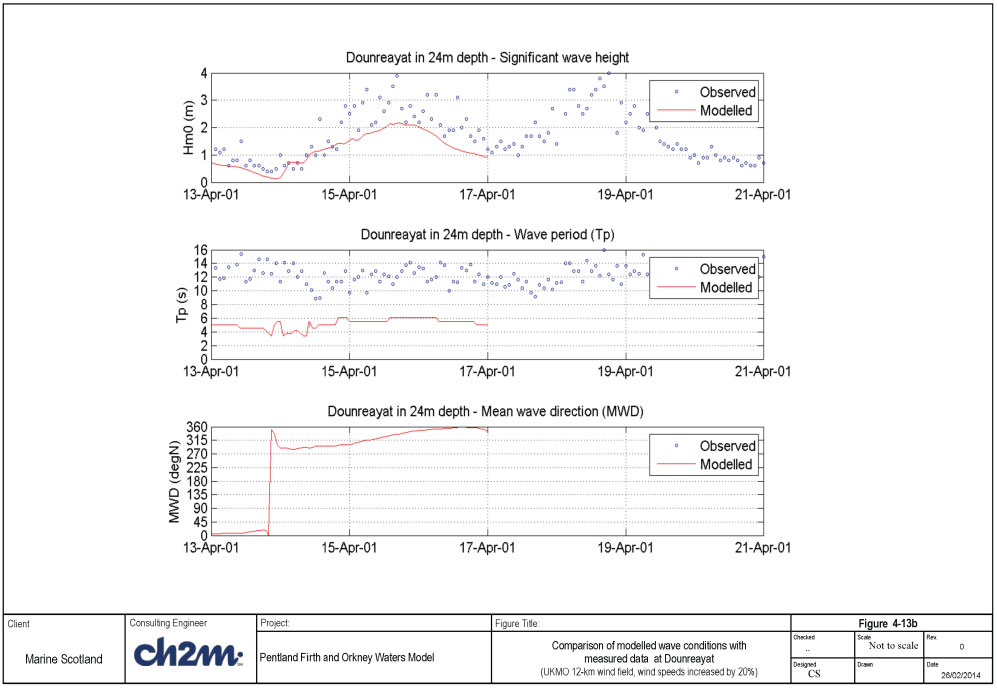
4.3.6.2 April 2001 simulation - Dounreay

A number of model runs were carried out to calibrate the wave model against measured data at Dounreay. Results from two selected runs are presented in this Section, which illustrate the effects of input wind dataset, and model sensitivity to the wind input and whitecapping source term formulation. The model runs are carried out for the period 12-April 00:00 to 16-Apr 23:00, including a 24-hour model spin-up period. The selected model runs are:

• Run 2F: 4-point wind; Komen wind input; Komen whitecapping
• Run 2J: 12km wind multiplied by 1.2 (Scaled 12km wind); Janssen wind input; Janssen whitecapping

Time series of wave conditions (during the simulated period) at the 4 UKMO points are shown Figure 4-12a, while the time series of wind conditions are shown in Figure 4-12b. It is difficult to pick out a definite storm during this event. The offshore Hm0 vary from 2.0 to 5.0m (mainly from West to North sector), with offshore wave period of approximately 7s. The wind speed is very variable at the 4 locations, with peaks of about 15m/s (in general) blowing from SW to NNW in the simulated period.

A summary of the model quality measures for these runs is shown in Table 4-7. Note that measurements of wave direction are not available at this site.

Table 4-7 Model quality measures at Dounreay for April 2001 runs (13 April 00:00 - 16 Apr 23:00).

Simulation Quality indices	Run 2F 4-point wind + Komen wi + Komen wc	Run 2J Scaled 12km wind + Janssen wi + Janssen wc
Hm0: Mean error, bias (m)	-0.48	-0.56
Hm0: RMS error (m)	0.64	0.67
Hm0: SI ( RMS/mean Hm0)	0.37	0.39
Hm0: Correlation coefficient	0.92	0.93
Tp: Mean error, bias (s)	-4.96	-4.67
Tp: RMS error (s)	5.22	4.83
Tp: SI ( RMS/mean Tp)	0.53	0.49
Tp: Correlation coefficient	-0.28	-0.21

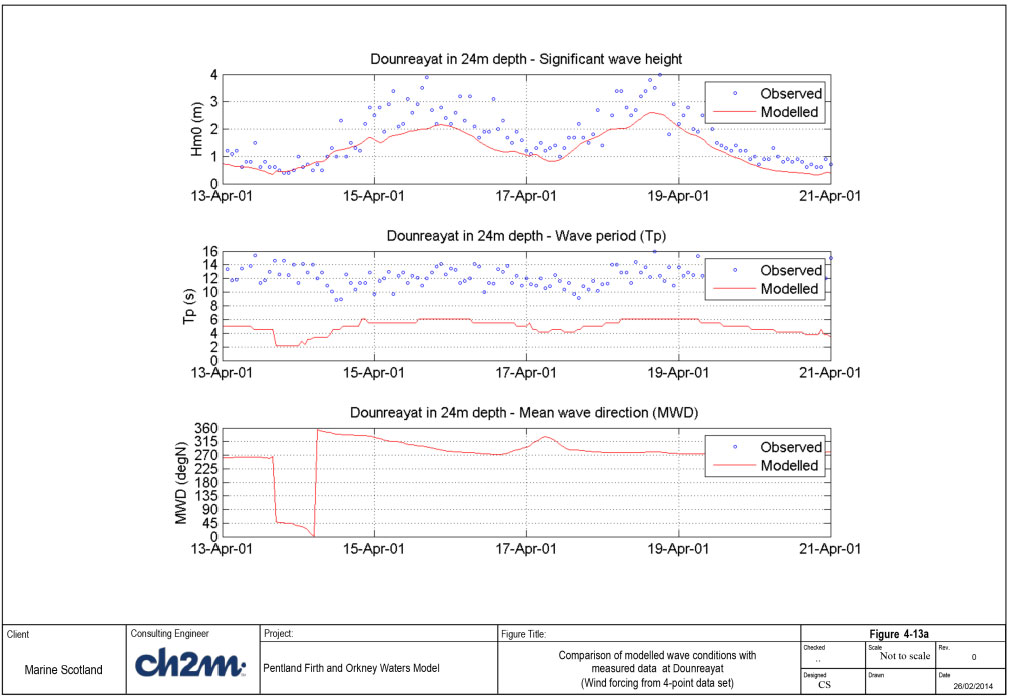
The modelled and measured wave conditions are shown in Figure 4-13a and Figure 4-13b for Run 2F (4-point wind data) and Run 2J (12km wind data) respectively. Table 4-7 shows a negative bias in the wave heights (that is, the modelled wave heights are generally lower than the measurements during the comparison period) of about 0.5m to 0.6m. Furthermore, the peak period is also significantly under-estimated (bias of about -5s). The under-estimation in the wave period comes from the specified offshore wave period (about 7s) as this site is an exposed site. With offshore wave period of about 7s, there is no mechanism in the wave model that can increase the wave period to 12s over the propagation distance. The fact that the offshore wave period is relatively short can partly explain the under-estimation of the wave height, since the effect of whitecapping dissipation is stronger for steep waves (which is the case here). Thus, this is likely the best comparison that can be obtained with the available offshore boundary wave conditions for this event.

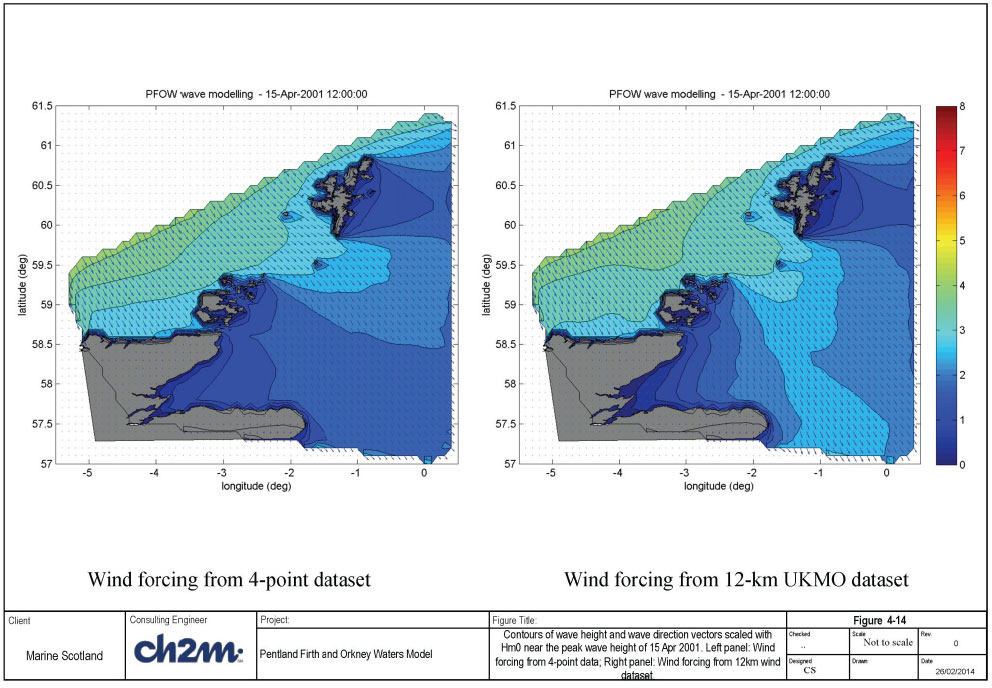
Figure 4-14 shows examples of two-dimensional contours of significant wave heights and wave direction pattern (scaled with wave height) at the peak of the storm. The left panel shows the result using the 4-point wind data, while the right panel shows the result using the scaled 12-km wind data.

4.3.6.3 Jan 2004 simulation - Holm Sound

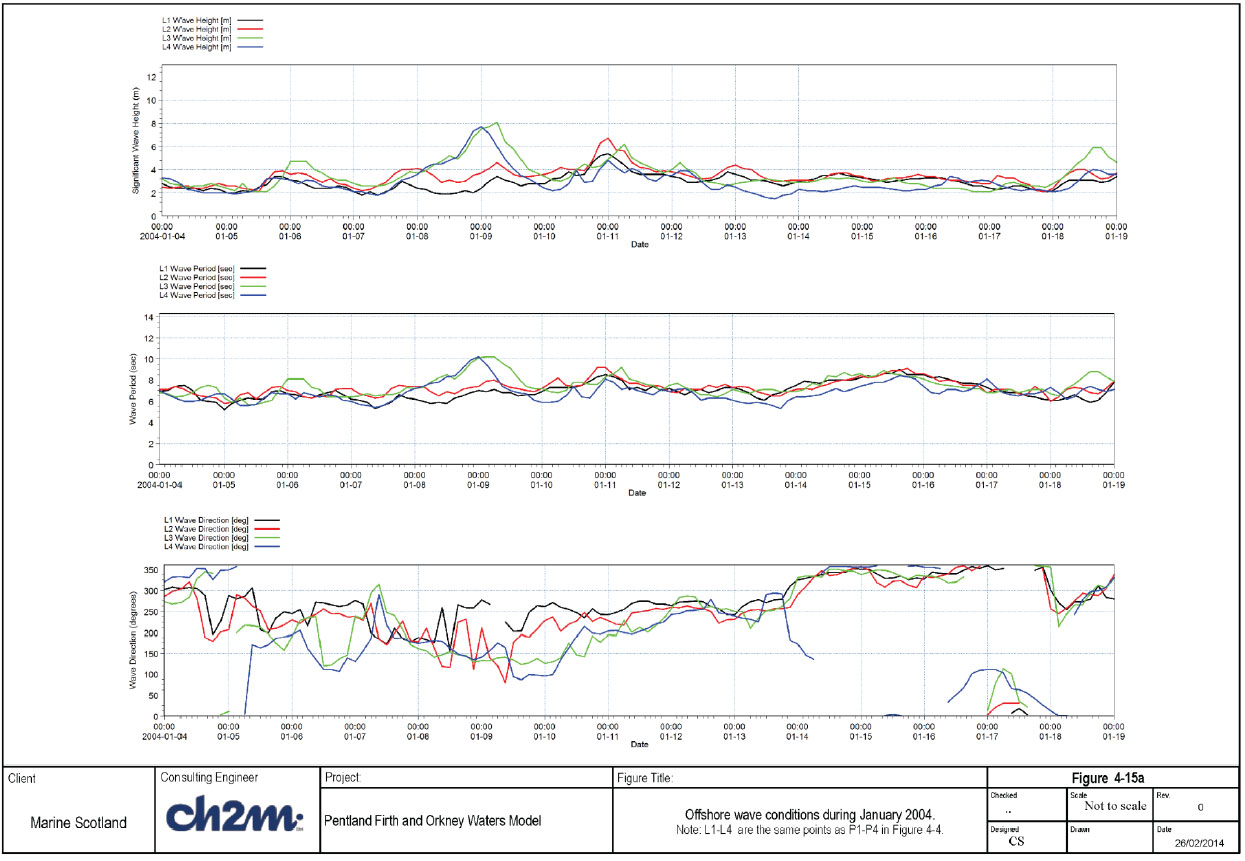
A number of model runs were carried out to calibrate the wave model against measured data at Holm Sound. Results from two selected runs are presented in this Section, which illustrate the effects of input wind dataset, and model sensitivity to the wind input and whitecapping source term formulation. The model runs are carried out for the period 04-January 00:00 to 18-January 23:00, including a 24-hour model spin-up period. The selected model runs are:

• Run 3C: 4-point wind; Komen wind input; Komen whitecapping
• Run 3D: Scaled 12-km wind; Janssen wind input; Janssen whitecapping

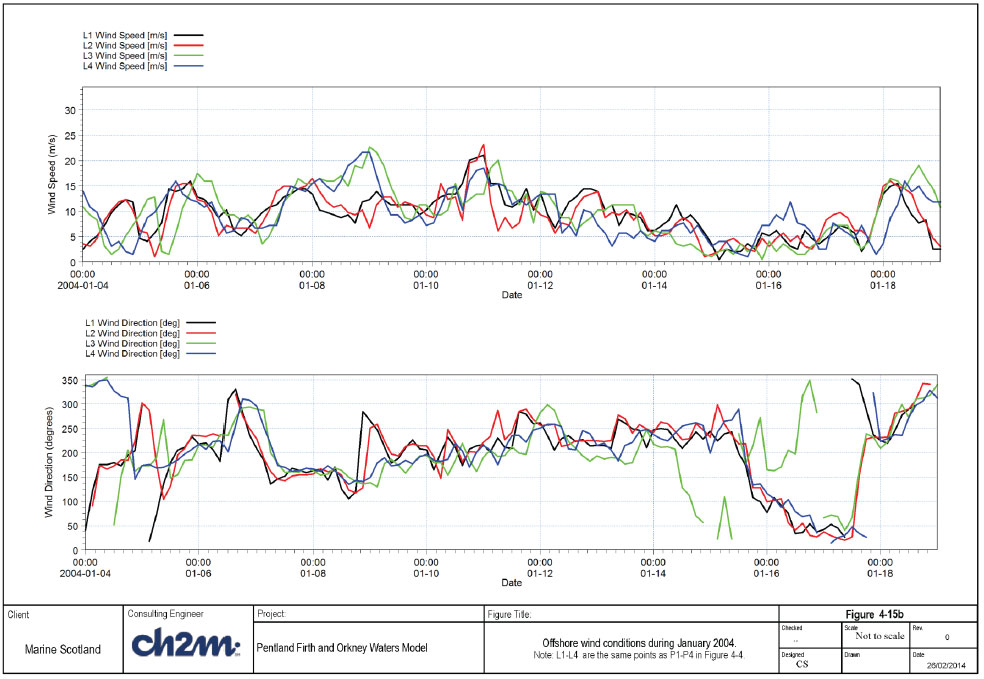
Time series of wave conditions (during the simulated period) at the 4 UKMO points are shown Figure 4-15a, while the time series of wind conditions are shown in Figure 4-15b. The largest storm during the simulation period occurred on 08-09 January 2004. The maximum offshore wave height during the storm is about 8m, coming from SSE (at position P4/L4) and with wave period of 10secs. The corresponding wind speed is about 22m/s from S to SSE sector.

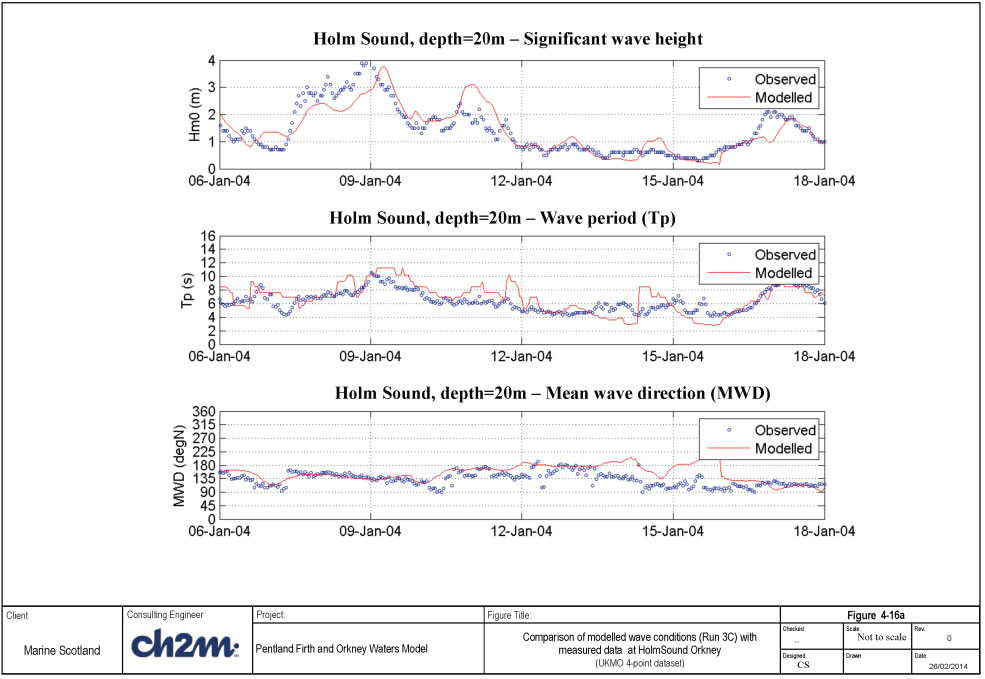
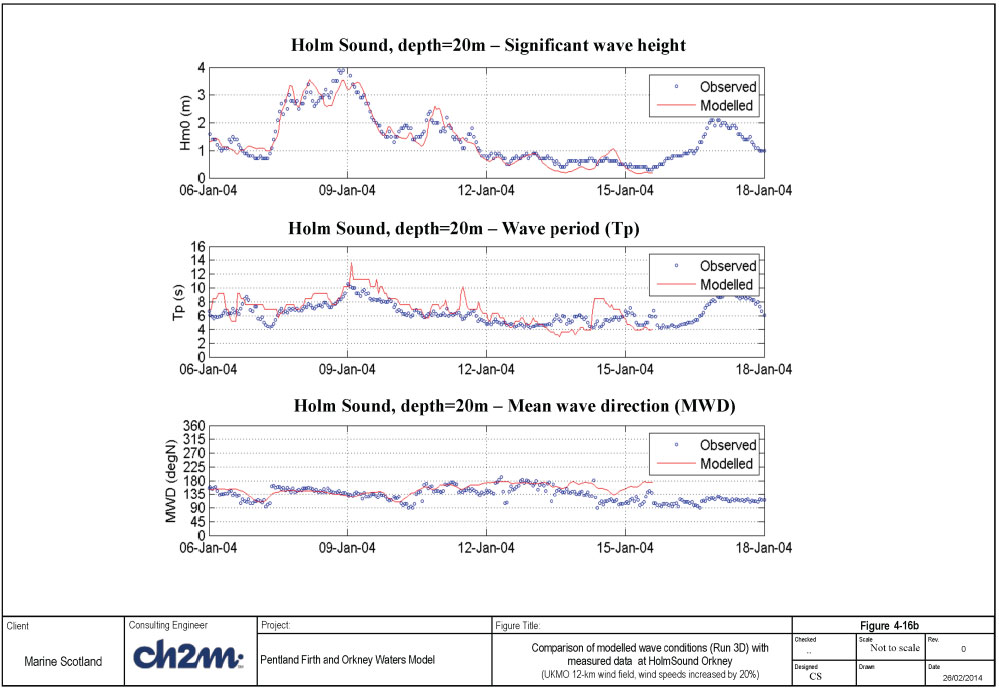
A summary of the model quality measures for these runs is shown in Table 4-8. The modelled and measured wave conditions are shown in Figure 4-16a and Figure 4-16b for Run 3B (4-point wind data) and Run 3D (scaled 12km-grid wind data) respectively.

The observed peak significant wave height during the storm is about 4.0m, while the corresponding modelled wave height is about 3.8m (Run 3C) and 3.5m (Run 3D). The peak wave height occurs slightly later in the model forced with the 4-point wind data (Run 3C). This phase error is corrected in Run 3D with the use of the scaled 12km wind fields. Visual comparison between the modelled and measured data shows that the model prediction of the wave height, wave period and direction are significantly improved in Run 3D. This calibration is considered to be satisfactory.

Table 4-8 Model quality measures at Holm Sound for Jan 2004 runs (05 Jan 00:00 - 18 Jan 23:00).

Simulation Quality indices	Run 3C 4-point wind + Komen wi + Komen wc	Run 3D** Scaled 12km wind + Janssen wi + Janssen wc
Hm0: Mean error, bias (m)	0.02	-0.10
Hm0: RMS error (m)	0.48	0.35
Hm0: SI ( RMS/mean Hm0)	0.35	0.26
Hm0: Correlation coefficient	0.85	0.94
Tp: Mean error, bias (s)	1.71	1.75
Tp: RMS error (s)	2.35	2.36
Tp: SI ( RMS/mean Tp)	0.47	0.48
Tp: Correlation coefficient	0.67	0.75
Dir: Mean error, bias (deg)	23.47	9.67
Dir: RMS error (deg)	41.77	24.66
Dir: SI ( RMS/mean Dir)	0.31	0.18
Dir: Correlation coefficient	0.28	0.38

**Run 3C completed to 15 Jan 14:00, and indices calculated to for corresponding period.

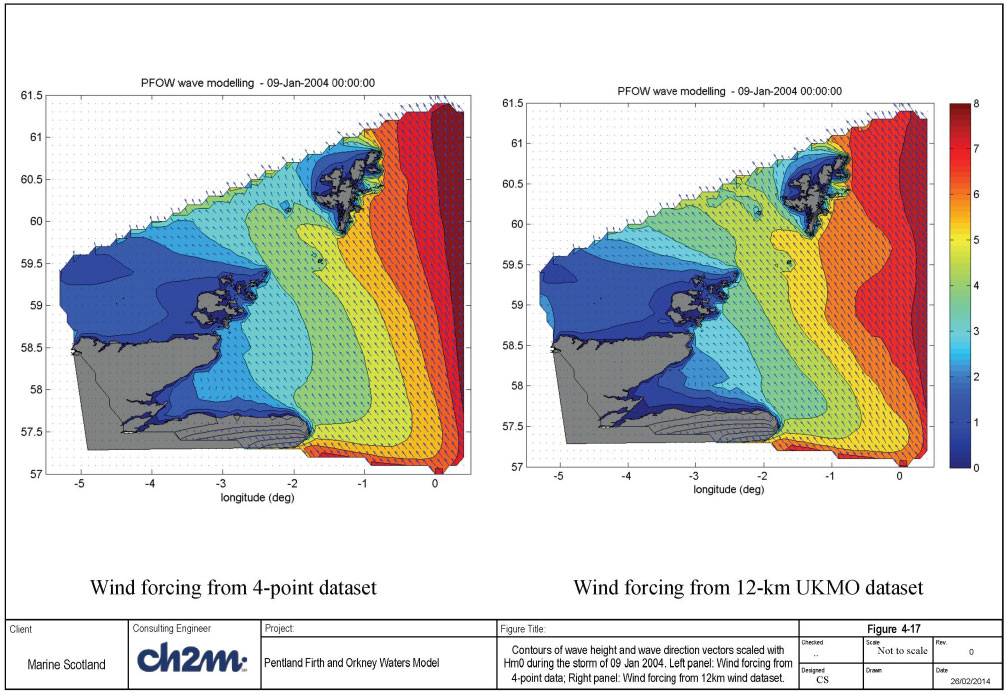
Figure 4-17 shows examples of two-dimensional contours of significant wave heights and wave direction pattern (scaled with wave height) at the peak of the storm. The left panel shows the result using the 4-point wind data, while the right panel shows the result using the scaled 12-km wind data.

4.3.7 Summary & Conclusions

A wave model for the Pentland Firth and Orkney Waters ( PFOW) has been constructed using the FVCOM- SWAVE. The model has been calibrated using measured wave data at Scapa Flow, Dounreay and Holm Sound. The comparison between the modelled and measured wave data at Scapa Flow and Holm Sound are considered to be satisfactory. The correlation coefficient for wave height is above 0.85 at all three locations.

However, the model generally under-predicts wave heights at Dounreay. A close examination of the offshore wave conditions during April 2001 shows that the offshore wave periods are significantly lower than the measured wave periods at Dounreay. Assuming that the measured wave periods are correct, the limitation in the offshore wave data is a plausible explanation for the under-prediction at this site.

The calibration shows that the wind input and whitecapping source terms are best described using the Komen formulation if the 4-point wind data is used to force the model. The Janssen formulation was found to be better when using the high resolution wind data (12km wind data). Furthermore, the scaled 12-km wind data provides improved results compared to the measurements.

4.4 Wave model simulations

Deliverable CS 1(a) in the Invitation to Tender ( ITT) requires a wave model to be setup and calibrated in order that seasonal conditions and specific periods of interest can be simulated. For this purpose the spectral wave model FVCOM- SWAVE has been used, and the model has been setup and calibrated as described in Section 4.3. Deliverable CS 1(a) also require that the model should deliver an assessment of the wave energy available for extraction.

Deliverable CS 1(b) requires that a year-long simulation using idealised forcing is undertaken for waves. For this simulation, a representative year was selected from analysis of the available boundary wave data (P1 to P4, see Figure 4-4). The representative year was selected using the methodology described in Section 4.4.1.

4.4.1 Selection of representative year

As stated above, one of the deliverables in CS 1(a) is that the model should deliver an assessment of the wave energy available for extraction.

The standard method of assessing wave energy resources is to carry out long term wave simulations (over several years) or use long term wave data available from reputable wave data supplier such as UK Meteorological Office. The long term wave data are used to determine available wave energy resources by determining the average annual, monthly and seasonal wave power (averaged over the number of years simulated) at all computational points in the model area. This approach was used in a number of previous studies (for instance, ABPmer (2008) to determine wave energy resources in UK waters; EMEC, 2009; WERATLAS, 2007, Wave Energy Centre, 2010). These studies typically cover a large area with fairly coarse model resolution, for instance, ABPmer (2008) used data from the Met Office UK Coastal Waters model with 12km resolution.

Recently, ABPmer (2012) used the same method to determine wave energy resources over the Pentland Firth and Orkney Waters Strategic Area ( PFOWSA) by simulating wave conditions over a 20year period (1990-2009). However, the area of coverage of the PFOWSA model is small in comparison to the model area covered in the present study. Similarly, Neill et al (2014) carried out wave simulations over a 10 year period (2003 -2012) to assess wave energy resources over the PFOWSA area.

For this study, the area covered by the PFOW model is relatively large and the model spatial resolution is also quite high (0.25 km to 1.0 km in the Pentland Firth and Orkney Waters). This results in excessive computational resource requirements (4 days simulation per month, using 60 cores on the computer cluster at the Hartree centre [http://community.hartree.stfc.ac.uk/wiki/site/admin/Home.html]) which is considered impractical for carrying out long term simulations. An alternative approach was therefore devised with the aim of ensuring that a realistic measure of the average annual wave energy resources is derived in a way that is computationally practical. A representative year approach was devised, which is an extension of a method used by Johnson et al (2001) to select representative annual wave conditions for sediment transport studies.

The aim is to determine a "representative year" from the available 12-year time series (2000-2011), such that the wave power determined from the selected year is broadly representative of the average available wave power over the 12-year period. The selected year is chosen to be broadly representative in terms of the annual, monthly and quarterly wave power and the directional distribution of the wave power. This method is referred to as the representative year approach, in contrast with the multiple year simulation approach used in previous studies.

The representative year has been determined using the wave data obtained from UK Met Office ( UKMO) at four locations around the study area. The methodology outlined below has been used:

• 1. The time series of available wave power per metre of wave crest, P was calculated as:

P = E*Cg, (4.1)

where E = 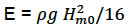is the wave energy, C _g = C _g(T _e, h) is the wave group velocity calculated as a function of wave energy period (T _e = m _-1/m ₀) and water depth (h), is the density of seawater (1025 kg/m ³), g is acceleration due to gravity (9.81m/s). Wave energy period, T _e has been calculated as: T = Tp/1.2 (this assumption is reviewed in Section 5.3), Tp is the peak wave period and C _g is calculated from the linear wave dispersion relation. The units of P is in W/m crest.

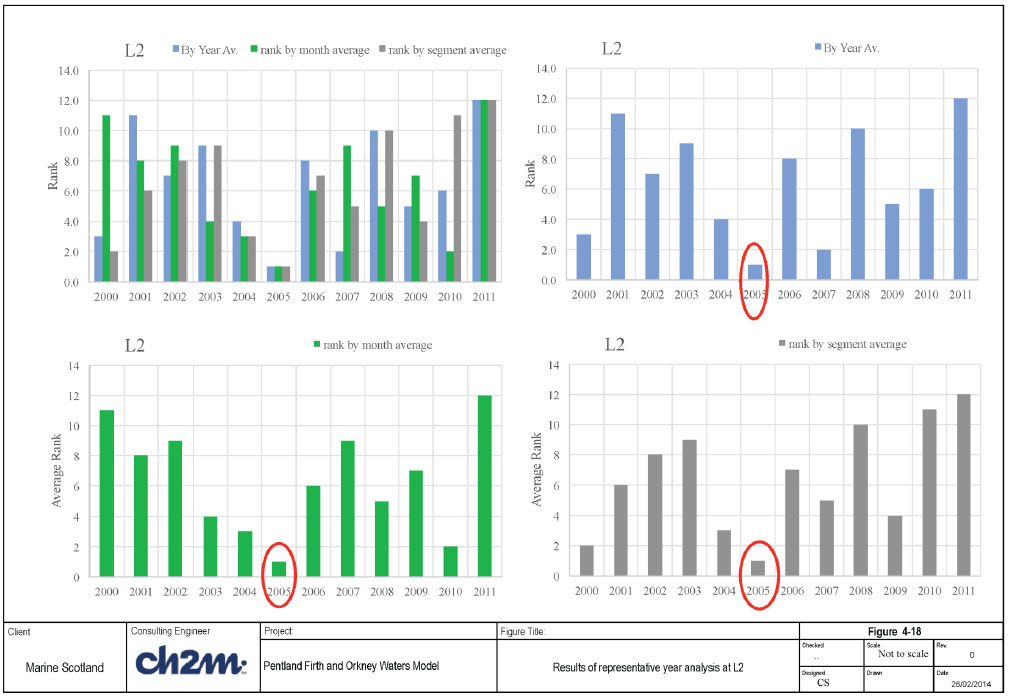
• 2. The average annual wave power for each year was calculated along with the average annual wave power for all years. The years were then ranked based on their deviation from the average annual wave power for all years (Figure 4-18).
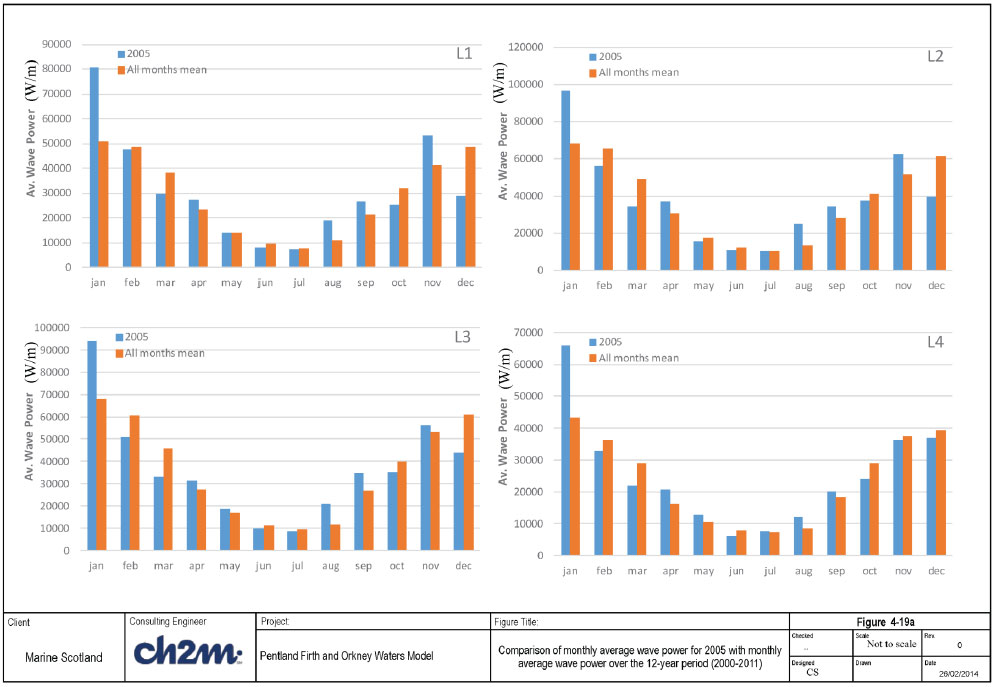
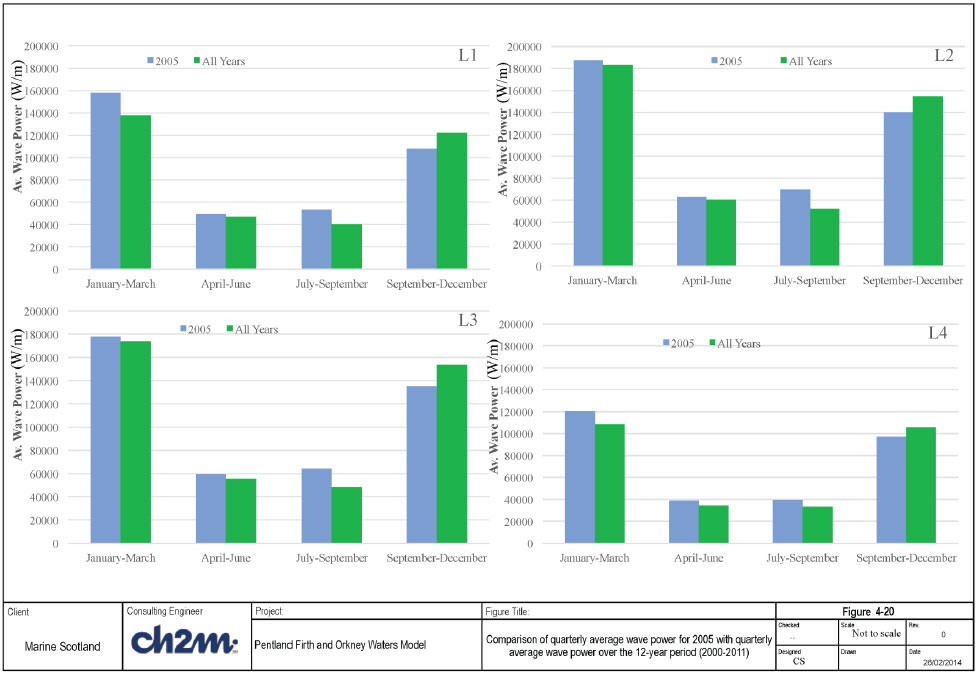
• 3. The average wave power for each month in each year was calculated as well as the average monthly wave power for the 12-year series. (For example, the average wave power for January was calculated for each year individually, then the average for all Januarys was calculated). The individual monthly averages were then ranked based on their deviation from the all-years average (Figure 4-19a). Similarly, the average quarterly wave power for each year was calculated and ranked based on their deviation from the overall average quarterly wave power (average for each quarter in the 12-yr time series). This is shown in Figure 4-19b.
• 4. The data was divided into 16 directional sectors (sector width of 22.5°), the process described above was repeated for the 16 sectors, i.e. the average wave power from each sector in each year was ranked against the average wave power from each sector for all years (Figure 4-20).

Ranking the years in terms of their deviation from the overall average provides an indication of which year falls closest to the average and hence a representative year. For the monthly and directional rankings, there are 12 and 16 values for each year respectively. This required simplification, therefore the ranks for each year were averaged and ranked from smallest to largest to give a single measure of fit for each year. The results of this analysis at L2 are shown in Figure 4-18 and a summary for all four locations is shown in Table 4-9.

Table 4-9 Summary of representative year analysis results at the 4 wave data locations

Location	Annual best fit			Monthly best fit			Directional best fit
	1 st	2 nd	3 rd	1 st	2 nd	3 rd	1 st	2 nd	3 rd
L1	2000	2005	2004	2010	2005	2004	2004	2000	2009
L2	2005	2007	2000	2005	2010	2004	2005	2000	2004
L3	2005	2007	2000	2004	2005	2007	2004	2005	2001
L4	2002	2004	2005	2004	2003	2001	2004	2001	2005

Table 4-9 shows that: a) year 2005 is the most representative of the annual wave power at the 4 locations, while year 2000 is second; b) year 2004 is the most representative of monthly distribution of wave power, while year 2005 is a second; and c) year 2004 is the most representative of the directional distribution of annual wave power, while year 2005 is second. Based on these results, 2005 was selected as the representative year.

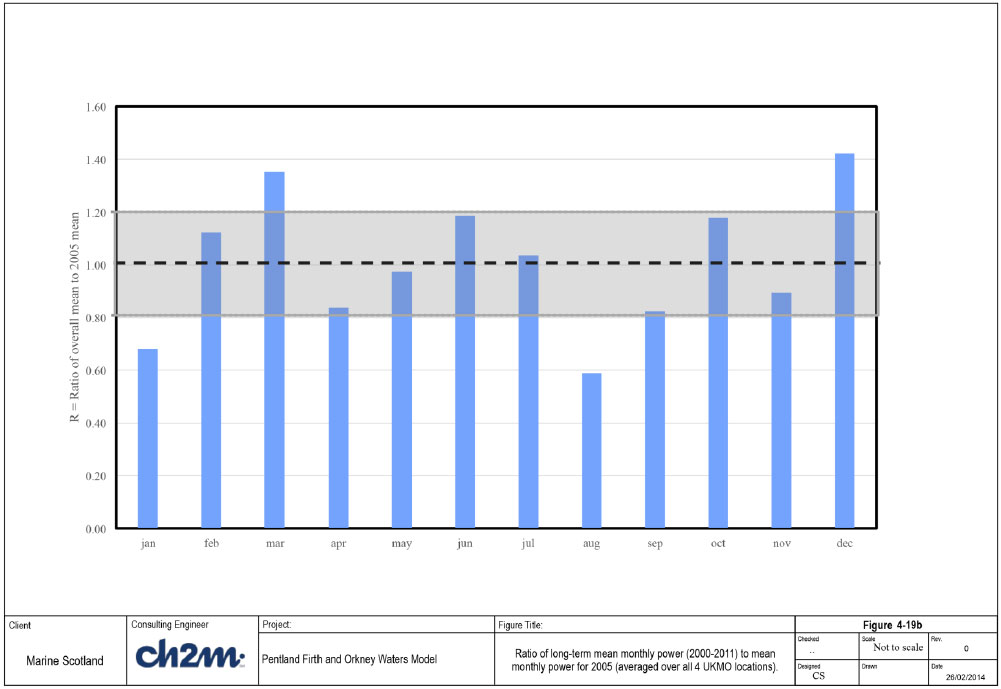
Therefore the wave energy resource throughout the model domain was determined using wave model results from 2005. The calculated mean monthly distribution of wave power for the representative year (2005) is compared with the mean monthly wave power for the entire record (2000 - 2011) at all the UKMO locations in Figure 4-19a. It is clear from this comparison that the monthly distribution of wave power in 2005 is different from the long term average. For instance, the wave power in Jan 2005 is significantly higher than the average for January, while the wave power for Dec 2005 is significantly lower than the average for December. In order to estimate the long term monthly average wave power from the 2005 simulation results, a scaling ratio (R) has been calculated at each UKMO station as:

R = Long term mean monthly wave power / mean monthly wave power for 2005

This ratio is averaged over all the four UKMO stations for each calendar month, and plotted in Figure 4-19b. The R values vary from 0.6 (August) to 1.4 (December), for a full list see Table 4-10.The calculated ratio is used to multiply the mean wave power calculated for each month in order to derive the best estimate of wave power for each individual month. Calculations show that the corresponding R for the entire year is approximately 1.0. Thus, the wave energy calculations for 2005 is the best estimate for the mean annual wave power.

Table 4-10 List of r values used for each month

Month	R at the four Met office data locations
	L1	L2	L3	L4	Average
January	0.63	0.71	0.72	0.66	0.68
February	1.02	1.17	1.19	1.11	1.12
March	1.28	1.42	1.38	1.33	1.35
April	0.86	0.83	0.88	0.78	0.84
May	1.01	1.14	0.91	0.84	0.97
June	1.18	1.16	1.13	1.29	1.19
July	1.05	1.00	1.14	0.96	1.04
August	0.57	0.54	0.55	0.69	0.59
September	0.81	0.81	0.77	0.90	0.82
October	1.27	1.10	1.14	1.21	1.18
November	0.77	0.83	0.94	1.03	0.89
December	1.68	1.55	1.39	1.07	1.42

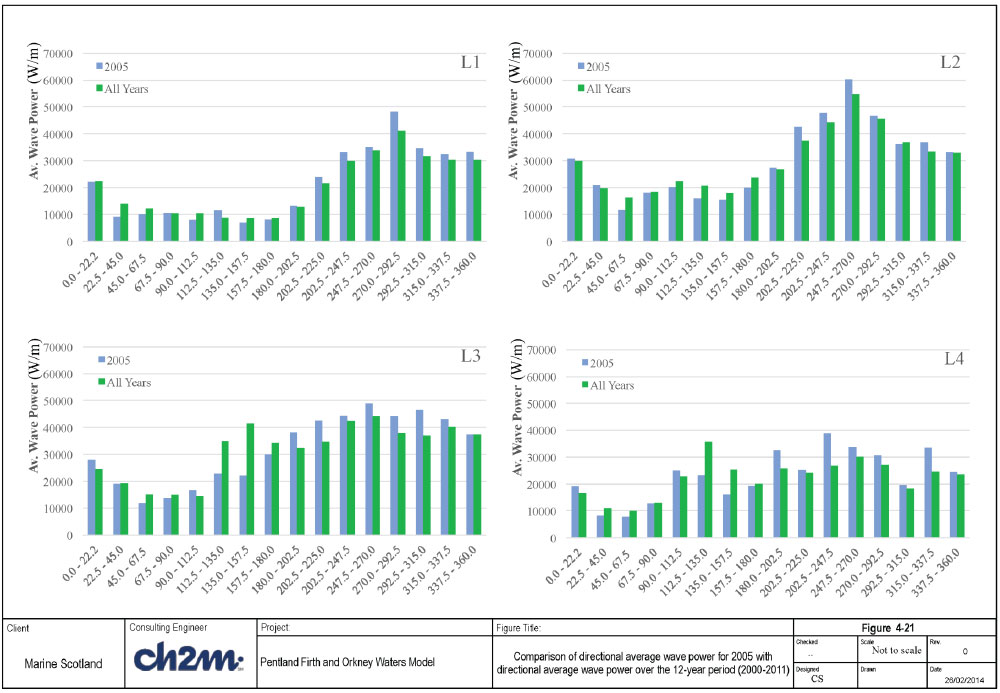
The comparison of mean wave power on a quarterly basis is shown in Figure 4-20, which shows fairly good agreement between the 2005 estimate and the long term average at all UKMO stations. The comparison of the directional distribution of wave power is shown in Figure 4-21. This shows a fairly good agreement between the 2005 directional distribution and the long term average at L1 and L2, although the agreement is not as good at L3 and L4. However, given that most of the wave energy comes from the sector of directions from SW and North, the wave energy coming from L1 and L2 are the most important. Hence, this is considered to be acceptable.

The wave model results for the simulated year is used to provide an estimate of the wave energy resources at the site. The estimated wave energy resources are subsequently compared with the results of previous studies.

4.4.2 Model simulations for the representative year

The parameters used in the wave model simulation for the representative year are the same as those derived from the final calibration simulations. The model parameters are summarised in Table 4-11.

The model results over the entire study area were archived at hourly intervals for the simulated year. The outputs include: a) significant wave height, H _m0; b) peak wave period, T _p and c) mean wave direction. In addition, hourly wave data (mostly) including wave spectrum were output at selected locations as shown in Table 4-12. The only exception to hourly data at the selected stations is the first three months (January to March), where the data is output every 3-hours.

Table 4-11 Wave model setup parameters

Parameter	Value
Frequency grid:	JONSWAP shape, f_low= 0.05; f_high = 0.5, No of frequencies = 24
Direction grid:	Cos^5 spreading, D_low= 0; D_high = 360, No of discrete directions =24
Forcings:	Boundary waves: UKMO wave data at 4 locations (2005) Wind conditions: UKMO 12-km resolution wind data (2005). A multiplication factor of 1.2 was applied to the wind speeds.
Water level:	0.0m (i.e. MSL)
Model physics	Wind Generation: GEN=3, GROWTH= JANS, AGROW=F Bottom Friction: Jonswap formulation, Cfw=0.015, Cfc=0 Whitecapping: WCAP= Janssen Wave breaking: alpha=1, gamma=0.73 (Battjes & Janssen) Wave-wave interaction: Quadruplet wave interaction
Time steps:	Flow part OFF in Waves ONLY run, but should be specified External timestep = 1s; ISPLIT= 6 Waves part Propagation: NS_DELTC = 12.0s Source terms: DTMIN = 1.0, DTMAX = 12.0s
Others:	Minimum water depth = 1.0m Nautical=True PWTAIL=4 (Non-diagnostic high frequency tail)

Table 4-12 Output locations for wave spectrum

Location ID	Longitude ( oE)	Latitude ( oN)
WN1a	-4.290	58.620
WN2a	-3.434	59.051
WN2b	-2.911	59.470
WN3a	-1.374	59.796
WN3b	-1.410	60.008
Billia Croo East Buoy (2010-2012)	-3.391	58.971
Billia Croo Offshore	-3.431	58.981
Falls of Wareness	-2.820	59.140
West PF	-3.291	58.718
Mid PF	-3.089	58.715
East PF	-2.937	58.650
Costa Head	-3.280	59.210

The model results for the representative year were further processed to determine wave energy resources at the at the project site. These results are presented and discussed in Section 5.3. Furthermore, the influence of wave-current interaction on the wave energy resources in the PFOW area has been assessed and discussed in Section 5.3.

4.5 Summary and Further work

A wave model has been developed and calibrated against measured data at 3 locations in the model area. The wave model calibration achieved a high degree of correlation (> 0.85) at the three measurement stations, which is considered satisfactory. Further improvements can be made in subsequent work (outside of the present study) to reduce the small negative bias in wave height predictions. Some suggestions to investigate include: a) increasing the 12km winds by a factor of 1.3 to 1.4 to determine the optimal scaling factor; b) reducing the rate of whitecapping dissipation; c) use of spectral data from a larger FVCOM SWAVE model or other similar models to investigate the impact of mixed sea and swell and d) use of additional boundary data points to better describe the boundary wave conditions.

Analysis of wave energy flux (wave power) at the four boundary data locations has been used to select a representative wave year. The representative year has been selected as Year 2005. And wave simulations have been carried out for the representative year. The results of the representative year simulations has been used in Section 5.3 to assess wave energy resources in the PFOW area.