Economic impacts for Scottish and UK seafood industries post-Brexit: report

Appendix D: Trade Model Details

D.1 Model equations

We begin by firmly grounding the model in standard consumer theory. Consider a market with n products from different countries: X ₁ , ..., X _n . We can introduce composite good made from all of the competing products:

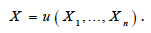
This gives as a quantity-index of consumption in given market, which can be viewed as a utility function of a representative consumer. We assume that u has generalised CES form:

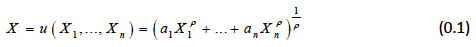
where a _n are called CES weights and p is a constant less than one.

If we combine it with budget constraint ,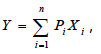

we can set up a dual-viewing consumer as choosing a consumption bundle that minimises the level of expenditures while retaining specific level of utility. The problem then becomes:

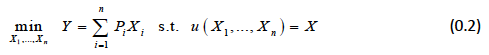
To solve it we set up the Lagrangian:

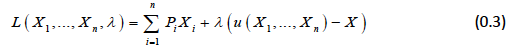
Differentiating the above expression, we can obtain the conditions for an optimal solution:

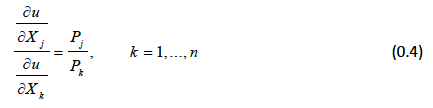
This means that the marginal rate of substitution between two goods equals their price ratio. In our case, the marginal utility for good X _i equals:

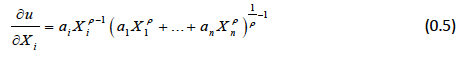
Which gives us:

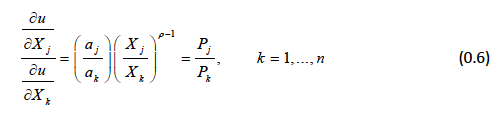
Solving for X _k we obtain:

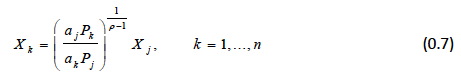
The elasticity of substitution between X _k and any other product competing in the market is constant and equal to :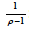

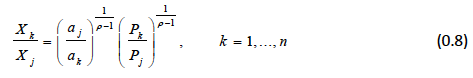
We assume 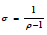, then the preceding simplifies to:

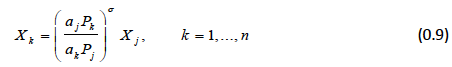
We can now use the final equation arising from using Lagrange method:

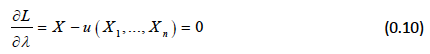
Substituting and rearranging gives us:

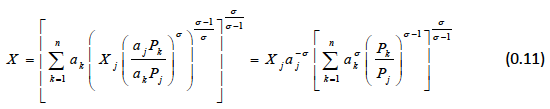
Solving for the X _j we obtain the Hicksian demands:

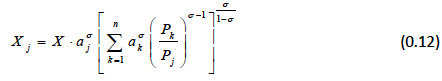
This can be simplified using the property arising from Armington (1969) assumptions:

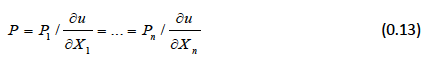
where P is an exact price index corresponding to the cost of a unit of utility. Substituting the relevant derivatives leads to:

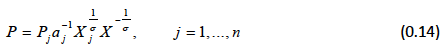
Substituting for X _j and rearranging:

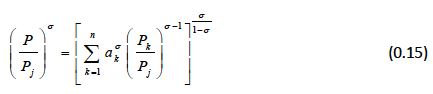
That along with the linear homogeneity of the utility function permits us to write the demand in a more compact form:

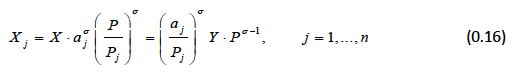
To obtain the price index P we need to calculate the expenditure function for a unit of utility:

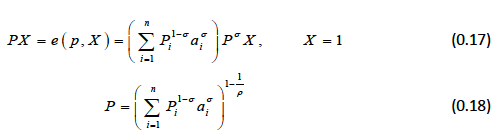
We then assume a supply function with a constant supply elasticity, and setting this equal to demand, we obtain excess demand conditions for each of the products:

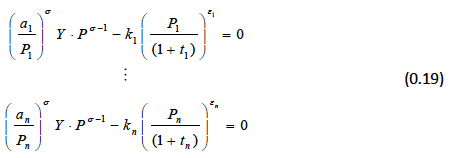
where: k _i are supply constants, t _i are aggregated trade barriers and 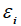are supply elasticities. Adding the excess demand condition for composite good:

and the price index equation:

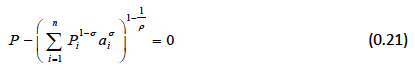
The model is summarised in Table D.1.

Table D.1. Model summary

Aspect	Detail
Variables:		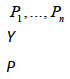Product prices Y Total expenditure P Composite good price index
Parameters (calibrated):		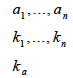CES weights Supply constants Demand for composite constant
Parameters (data):		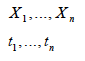Base trade flows Base tariffs
Parameters (assumed):		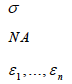Elasticity of substitution Composite elasticity of demand Elasticises of supply

D.2 Key parameters of the model

The price elasticity of demand for the aggregate product (Na), tells you, for a given fish species such as cod, how responsive demand for cod is, as the price of cod changes.

The elasticity of substitution (Sig) between individual product varieties from different sources tells you if the price of (for example) UK cod changes, the extent to which cod from other sources (e.g. Russia) is a substitute. The higher the elasticity of substitution, the easier it is for consumers to switch to other sources. In the model the elasticity of substitution is treated as being the same across different sources. Hence the degree of substitutability between e.g. UK and EU sources, is the same as between UK and Chinese sources. For the elasticity of substitution there are no detailed information available. We have assumed that this is equal to 5 for most of the species, except for crab, Nephrops, and scallops where we have assumed 2.5, as EU imports of these species from the UK focus on fresh product.

Note that in the work of the United States International Trade Commission ( USITC) (Donnelly et al., 2004), which bases much of its work on the Global Trade Analysis Project ( GTAP) dataset, the elasticities they use are:

• “prepared fresh or frozen fish and seafoods” = 1.7; and
• “canned and cured fish and seafoods” = 5

The price elasticity of supply (Es) captures how easy it is for supply to respond to changes in price. The higher the elasticity the easier it is for supply to increase for any given change in price. Another way of putting this is that the higher is the elasticity, as supply changes the price changes by less. The elasticity of supply could be set differentially for each supplier. The elasticity has been set = 1 for all suppliers and all species. Note that Pascoe and Mardle (1999) estimate supply elasticities for a range of fish species and find short- and long-run supply elasticities of less than one for each of the species, with the highest long-run elasticity being for Haddock (0.86), and the lowest for Cod (0.11).

Data on each of the above are limited, especially with regard to fish. There are a few papers that give some estimates for the price elasticity of demand for fish in aggregated form with numbers typically around 1.5 (e.g. Andreyeva et al., 2010; Muhammad et al., 2013), but with some variability. One of the few papers that provides detailed estimates is the work of Kee et al. (2008). Hence for the overall elasticity of demand we are using this work. They provide extremely detailed estimates of import demand elasticities at the HS 6-digit level, and by country. We have taken their median elasticity (across countries) for each of the relevant HS 6-digit fish categories for each of our species. The average elasticity is then a weighted average, where the weights are the shares of total trade of each category in UK trade.

Detail of the parameter values used in the model are provided in Table D.2.

Table D.2. Parameters used in the model

Species	Summary Information
	MFN Tariffs	EU-Norway Tariffs	Changes in Quotas	Elasticity of Demand	Elasticity of Substitution	Elasticity of Supply
Cod	11.5	0.57	8.8%	5.43	5	1
Crab	7.8	2.27	-	4.14	2.5	1
Haddock	7.5	0.3	21.2%	0.44	5	1
Hake	12.3	3.3	166%	1.14	5	1
Herring	14.3	6.8	219%	2.83	5	1
Mackerel	14.5	9.7	53.4%	2.24	5	1
Nephrops	16	1.6	4.8%	0.64	2.5	1
Saithe	7.5	0.3	186%	0.41	5	1
Salmon	4.9	4.1	-	0.71	5	1
Scallop	16	7.6	-	0.72	2.5	1

D.3 References

Andreyeva, T., Lond, M.W. & Brownell, K.D. (2010). The impact of food prices on consumption: a systematic review on research on the price elasticity of demand for food. American Journal of Public Health 100: 216–222.

Armington (1969). A Theory of Demand for Products Distinguished by Place of Production. Staff Papers (International Monetary Fund). Vol. 16, No. 1 (Mar., 1969), pp. 159-178.

Donnelly, W.A., Johnson., K., Tsigas. (2004). “Revised Armington Elasticities of Substitution for the USITC model and the concordance for constructing a consistent sent for the GTAP model”, USITC, Office of Economics Research Note, No. 2004-01-A.

Kee, H.L., Nicita, A. & Olarreaga, M. (2008). Import Demand Elasticities and Trade Distortions. Review of Economics and Statistics 90 (4): 666–682.

Muhammad, A., Seale, J.L., Meade, B. & Regmi, A. (2013). International evidence on food consumption patterns: an update using 2005 international program data. TB-1929. U.S. Dept. of Agriculture, Econ. Res. Serv. March 2011. Revised February 2013

Pascoe, S., and Mardle, S., (1999). “Supply response in fisheries – the North Sea”, University of Portsmouth Research Paper, no. 143.