Consultation regarding the redraw of Data Zones

11. Calculation of the Data Zone Centroid

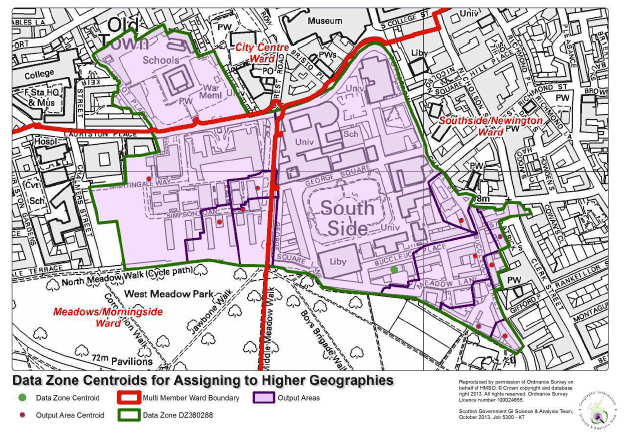
11.1. The Data Zone centroid represents the centre of the area. This is not the geometric middle of the Data Zone, but a point that represents the population centre. The main use of the centroid is to determine which higher level geography the Data Zone would be allocated to. Figure 1.8 shows an example of this, where a 2011 Data Zone (labelled DZ360288) crosses Multi Member Ward boundaries of City Centre, Southside/Newington, and Meadows/Morningside in Edinburgh. In this case, the Data Zone centroid falls within the Southside/Newington ward, so for reporting and aggregation purposes would be assigned to this ward.

Fig 1.8: The centroid is used to assign Data Zones to higher geographies

11.2. For 2001 Data Zones, centroids were calculated as the population weighted centre (essentially the mean centre) of all 2001 Census Output Areas contained within the Data Zone. The methodology used can be found here:

http://www.scotland.gov.uk/Resource/Doc/933/0082884.doc

11.3. For 2011 Data Zones, we are proposing a small change in the methodology used to calculate the Data Zone centroid. The methodology remains broadly the same, but instead of using the population weighted mean, we are proposing to use the output area median.

11.4. The median is a measure of central tendency and, broadly speaking, the median can be thought of as the 'middle' value. While the mean is calculated by summing all the values together and then dividing by the number of observations, the median is calculated by putting the observations in order, from lowest to highest, and then taking the value in the middle. (Or calculating the mean of the two middle values if there are an even number of observations.).

11.5. The key advantage of using the median is that it is not as heavily influenced by extreme values as the mean. If a Data Zone has a highly skewed population distribution, for example a large rural data zone containing a small town in one corner, then the mean can be heavily influenced by the small number of people who live far away from the population centre and the mean will likely fall outside of the town. The median is considered to be a more robust measure of central tendency and is less likely to be influenced by values far away from what would be considered to be the population centre of the Data Zone.

11.6. The process for creating 2011 Data Zone Centroids was automated using ESRI ArcGIS, but the general method is described below:

1. The median easting and northing coordinate pair for all Census Output Areas within the Data Zone is calculated, giving a notional centroid of the Data Zone.
2. Data zones can be complex shapes, so to ensure that the median falls within the data zone boundary, a second step is carried out move it to the nearest output area centroid. The distance from each of the Census Output Area centroid to the median easting/northing is calculated using Pythagoras' Theorem. The Census Output Area coordinate pair with the shortest distance to the median was chosen to represent the centroid of the Data Zone.

11.7. For the purposes of the consultation, centroids using both the mean and median methods have been created for review. Of the 6,940 centroids, 1,431 differ in location between the mean and median methods. Differences occur in all councils except the Western Isles and Glasgow. The council with the greatest discrepancy is Dumfries and Galloway, where 35% of centroids fall in a different location depending on whether the mean or median method is used.

11.8. The differences in the locations of the centroid may have an impact on the Data Zones assignment to a higher level geography. For example, 6 of the 2011 Data Zones would be assigned to a different 2001 Intermediate Zone, and 28 would be assigned to a different Multi Member Ward.

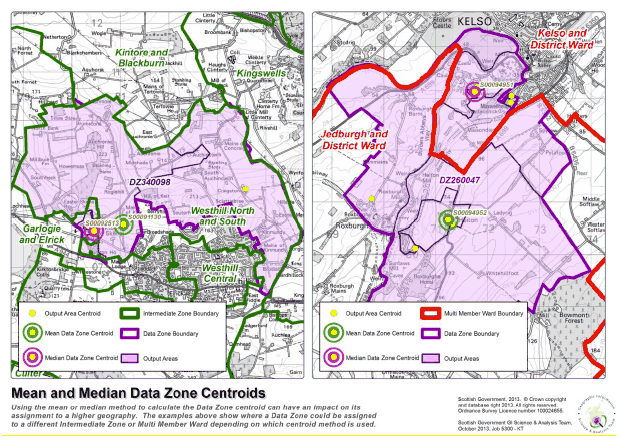
11.9. Figure 1.9 shows two examples of where the mean and median centroid could impact higher geography assignments. The 2011 Data Zone on the left hand map (labelled DZ340098) would be assigned to the Westhill North and South Intermediate Zone using the mean centroid, however, it would be assigned to Garlogie and Elrick if the median centroid is used. The map on the right shows how data zone DZ260047 would be assigned to the Jedburgh and District Multi Member ward if the mean centroid is used, but would be assigned to Kelso and District ward if the median is used.

Fig 1.9: The mean and median centroids may lead to differences in higher geography assignments for some data zones

11.10. Consultation Question:

Do you agree that 2011 Data Zones should use the median methodology?

Other aspects for consideration