Value of bathing waters and influence of bathing water quality: technical annex

Annex 3: Econometric analysis of online survey data – stated preference method

A-3.1 Introduction

This annex provides selected technical detail and results from the econometric analysis of the survey data to support the findings presented in the main report. This annex is structured as follows:

• Online survey sample profile ( section A-3.2); and
• Choice experiment analysis ( section A-3.3).

A-3.2 Online survey sample profile

Figures are rounded to nearest whole number which may cause totals to sum to more than 100%. The online survey consists of a sample of 1,013. Sample sizes are indicated within each of the subsequent tables. Where the indicated sample size differs from the overall survey sample size, this is explained by the routing of the surveys (see accompanying survey documents in Annex 6). Full summary stats for each question of the surveys are provided as accompanying excel documents to the report. Quotas were used in order to ensure a nationally representative sample. Overall, our data fits the quotas, however our weighting was also applied to our econometric models in order to mitigate any slight discrepancies (i.e. variations within 5% points).

Table A3-1: Respondent gender

Respondent gender	Online n %		Target quota %
Male	444	44 %	48%
Female	569	56%	52%
Total	1013	100%	100%

Respondent gender (drawing on data from online survey question 4)

Table A3-2: Respondent age

Respondent age	Online n%		Target quota %
18-24	77	8%	11%
25-34	133	13%	17%
35-44	160	16%	15%
45-54	197	19%	18%
55-64	205	20%	16%
65+	214	24%	23%
Total	1013	48%	100%

Respondent age (drawing on data from online survey question 5)

Table A3-3: Main income earner’s socio-economic group

Income earner’s socio-economic group	Online n %		Target quota %
AB	215	21%	19%
C1	340	34%	31%
C2	189	19%	24%
DE	268	26%	26%
Total	1013	100%	100%

Main income earner’s socio-economic group (drawing on data from online survey question 7)

Table A3-4: Ethnic group

Ethnic group	Online n	Online %
Scottish/English/Welsh/Northern Irish/British	933	92%
Irish	4	0%
Gypsy or Irish traveller	0	0%
Any other White background	43	4%
Mixed - White and Black Caribbean	0	0%
Mixed - White and Black African	3	0%
Mixed - White and Asian	5	0%
Any other Mixed background	0	0%
Indian	3	0%
Pakistani	7	1%
Bangladeshi	0	0%
Sri Lankan	0	0%
Any other Asian background	3	0%
Caribbean	1	0%
African	3	0%
Any other Black background	0	0%
Arab	0	0%
Any other ethnic group	2	0%
Prefer not say	6	1%
Total	1013	100%

Respondent ethnicity (drawing on data from online survey question 44)

Table A3-5: Number of people in household including both adults and children

Number of people in household	Online n	Online %
1 person	227	22%
2 people	466	46%
3 people	159	16%
4 people	117	12%
5 people	24	2%
6 people	10	1%
more than 6 people	9	1%
Prefer not to say	1	0%
Total	1013	100%

Number of people in household including both adults and children (drawing on data from online survey question 46)

Table A3-6: Age of household members

Age of household members	Online n	Online %
Aged 0 - 12 months	38	9%
Aged under 5 years	67	16%
Aged 5 - 10 years	134	33%
Aged 11 - 15 years	99	24%
Aged 16 - 18 years	63	15%
Prefer not to say	9	2%
Total	410	100%

Age of household members (drawing on data from online survey question 48)

Table A3-7: Household income

Household income	Online n	Online %
Less than £10,000	116	11%
£11,000 - £20,000	245	24%
£21,000 - £30,000	202	20%
£31,000 - £40,000	166	16%
£41,000 - £50,000	89	9%
£51,000 - £60,000	39	4%
£61,000 - £70,000	21	2%
£71,000 - £80,000	10	1%
£81,000 - £90,000	9	1%
£91,000 - £100,000	4	0%
Over £101,000	7	1%
Don't know	34	3%
Prefer not to say	71	7%
Total	1013	100%

Household income (drawing on data from online survey question 49)

A-3.3 Choice experiment analysis

The main feature of the online survey that explored attitudes towards improvements in bathing water quality was a choice experiment which required respondents to select their preferred option from three alternatives that traded-off changes in: (i) the number of bathing waters at the national level failing to meet ‘sufficient’ status (% bathing waters failing); (ii) the bathing water status of the beach they visit most often (‘poor’, ‘sufficient’, ‘good’ or ‘excellent’); (iii) the cleanliness of the beach they visit most often (% litter removed) ^[1] ; and (iv) the cost to their household to secure these improvements.

A-3.3.1 Consumer demand theory

The application of choice experiments is based on consumer demand theory. This assumes that the utility (benefit) derived from the provision of a ‘complex’ good is linked to the characteristics of the good. In this study the ‘good’ is represented by improvements in bathing water quality. Hence, the utility derived by each respondent is linked to the characteristics of the ‘good’.

The cornerstone of any stated preference method is the assumption that individuals know their own preferences and, whatever choice is encountered, they know what is best for them. In formal terms we can say that an individual (i) is assumed to choose alternative j over alternative k if the utility derived from attribute bundle j is greater than the utility derived from attribute bundle k; i.e. if U _ij > U _ik, where U _ij is the total utility associated with alternative j and U _ik is the total utility associated with alternative k. The utility function for respondent i related to alternative j is specified as:

U _ij = V _ij + ε _ij    [1]

where V _ij is the systematic (non-stochastic) utility function observed by the analyst because it is linkable to the attribute levels of each alternative (e.g. water quality levels) and _ij is a random component, which is known to the individual, but remains unobserved to the analyst. This random component ( _ij) arises either because of randomness in the preferences of the individual or the fact that the researcher does not have the complete set of information available to the individual.

A-3.3.2 Mixed logit model

For this analysis, it was appropriate to conduct a sophisticated econometric analysis and test less restrictive model specifications that relax some of the assumptions of a multinomial logit ( MNL) model. For example, by allowing for:

• Variations in tastes by respondents or decision-makers in relation to the observed characteristics;
• Correlation (non-independence) of unobserved factors in repeated choices by respondents; and / or
• Different variances across alternatives (or bundles of characteristics).

These are represented in the analysis by the random parameter logit ( RPL) model; the RPL-correlated model; and the Error-Component ( EC) model respectively. Collectively all these belong to the family of mixed logit ( MXL) models.

The utility structure for the RPL model is designed to allow for randomness in the taste across respondents. It is denoted as:

U _ij = x _ij' + ε _ij    [3]

where x _ij are observed variables that relate to the alternative (the attributes of the alternative and the levels of those attributes), is a vector of utility coefficients of these variables describing the weight each one carries in determining the utility of the alternative (hence representing the respondent’s tastes), and ε _ij is a random error term that is independently and identically distributed (iid) extreme value. This specification is the same as the MNL except that is now random and varies across individuals instead of being fixed at the same level for all respondents. Thus the RPL model allows coefficients to vary over respondents according to some distribution reflecting their tastes.

The basic RPL model assumes that random parameters are uncorrelated. Thus, it treats two responses by the same individual in the same way as it treats two responses from different individuals. The RPL-correlated model relaxes this assumption and allows for correlation among parameters (i.e. allowing for the likelihood that responses from the same individual are likely to be correlated). This therefore acknowledges that the data has a panel structure and that preferences are consistent in all choices made by the same respondent, changing only when another respondent’s choice is evaluated. The RPL-panel model thus accounts for any bias arising from correlation in the error term in choices by the same respondent.

The Error-Component model can be used to account for correlations amongst utility for different alternatives. In a choice between alternatives that are in-part hypothetical (e.g. improvements not previously experienced) and in-part experienced (current levels), it can be erroneous to assume that utility has the same variance in both types of alternatives. It can be argued that, since hypothetical alternatives need to be conjectured by all respondents, these are subject to higher variance than those alternatives that are experienced. One device to allow for a larger variance is by means of the introduction of additional error components, which also allow correlations amongst utilities for different alternatives. In these models utility is defined as:

U _ij = β’ x _ij + μ’ _i z _ij + ε _ij      [4]

where x _ij and z _ij are vectors of observable variables relating to alternative j, β is a vector of fixed coefficients, μ is a vector of random terms with zero mean, and ε _ij is an iid extreme value. The terms z _ij are error components, and along with ε _ij, represent the stochastic portion of utility. The unobserved random portion of utility, η _ij = μ’ _i z _ij + ε _ij, can be correlated over the alternatives. Failure to account for correlation and variance in unobserved factors between alternatives leads to coefficient bias in the MNL model.

A-3.3.3 Econometric estimation strategy

The estimation strategy focused on identifying the model specification that provided the best fit to the data; i.e. the model that provides the best account of respondents’ preferences for improvements in bathing water quality. The assessment of the comparative performance of alternative models was primarily based on their ‘information criteria’. Whilst alternative measures of model fit were also examined (log-likelihood and pseudo R2), the information criteria represent an appropriate basis for comparing model performance since this penalises more complex models for having a large number of parameters. In particular, models are estimated using maximum likelihood methods and, in these circumstances, a model with a greater number of parameters cannot return a goodness of fit that is worse than a model which is specified with a subset of the same parameters (i.e. including more model parameters improves model fit).

A-3.3.4 Expectations of results

Theoretical considerations and prior empirical results give rise to certain expectations for the parameter estimates in choice experiment models. In particular, these relate to the ‘sign’ of coefficient estimates (positive or negative), which inform on the nature of the relationship between a parameter – i.e. an attribute – and respondents’ preferences:

Level coded (linear) models - for variables coded in the levels, expectations for the signs of the coefficient estimates relate to the effect of increasing that variable by one unit of measurement. Since models are consistent with random utility theory of choice, those attributes whose units of measurement increase when an improvement occurs are expected to have a positive coefficient, thus indicating a positive effect on utility. For example, the removal of litter attribute is described in terms of the percentage of litter removed at the beach a respondent visits most often. A one unit increase implies that 1% more beach litter is removed at that beach. Therefore, the expected sign of the coefficient is positive.

Dummy coded (piecewise/non-linear) models - for variables that are dummy coded (sub-groups organised in such a way to be either a ‘1’ or a ‘0’), the expectations for the signs of the coefficients depend on the direction of the effect relative to the baseline. For effects that improve on the baseline the expected sign is positive, while for effects that detract from the baseline the expected sign is negative. In the context of this study, the baseline is “poor in 5 years”. The relative coefficients are expected to be positive.

A summary of expected coefficient sign for each attribute is provided in Table A3-8.

Table A3-8: Expected coefficient signs for attributes

Attributes	Expected sign
Bathing water status – poor	Negative
Bathing water status – good	Positive
Bathing water status – excellent	Positive
Litter - % removed	Positive
National - % bathing water failing sufficient	Negative
Cost - £ increase in water bill	Negative

Expected coefficient signs for attributes (drawing on data from online survey questions)

A-3.3.5 Model results

The results for the choice experiment model are presented in Table A3-9 below. The model used is a mixed logit ( MXL) model which is the ‘preferred’ model specification based on comparative assessment of model fit.

• Results from the choice experiment task accord with prior expectations and the analysis shows that, all else equal:
• Respondents prefer options that offer better bathing water quality, i.e. fewer beaches failing to meet bathing water quality standards;
• Respondents prefer options with improved bathing water quality for the beach they visit most;
• Respondents prefer options with removal of more litter for the beach they visit most; and
• Respondents prefer options with a lower cost to their household in terms of an increase in annual water bill.

Table A3-9: Choice experiment model results

Explanatory variable	Coefficient estimate	Standard error
Mean values
Bathing water status – poor	1.098***	0.008
Bathing water status – sufficient	1.626***	0.399
Bathing water status – good	1.902***	0.353
Bathing water status – excellent	3.500***	0.356
Litter - % removed	0.018***	0.671
National - % bathing water failing sufficient	0.038***	0.002
Status quo	-0.749*	0.008
Cost - £ increase in water bill	-0.041***	0.422
Standard deviation parameters
s.d Bathing water status – poor	-1.107	0.967
s.d Bathing water status – sufficient	-0.012	0.040
s.d Bathing water status – good	-0.015	0.013
s.d Bathing water status – excellent	3.185***	1.192
s.d Litter - % removed	-0.046***	0.007
s.d National - % bathing water failing sufficient	0.099***	0.021
s.d Status quo	0.050	0.185
Pseudo R 2		0.18
Sample size (observations)		1,013 (18,234)

*** indicates coefficient estimate is statistically significant at the 1% level, ** indicates coefficient estimate is statistically significant at the 5% level, * indicates coefficient estimate is statistically significant at the 10% level.

Based on analysis of the choice experiment responses, values for improvements in bathing water quality and beach characteristics – in terms of WTP per household and in total for national improvements – are presented in the main report and also reproduced in Table A3-10 . WTP for each attribute is determined by the ratio of the marginal utility associated with a one unit increase in the attribute and the marginal utility associated with a one unit increase in cost (i.e. in respondents’ water bill).

Table A3-10: Value of improvements in bathing water quality

Willingness to pay (WTP) estimates		£/household/year	Total WTP £ million / year
National - number of Scottish beaches failing to meet water quality standards - 1% reduction (roughly 1 less beach failing of the 86 Scottish bathing waters)		0.93 (0.49 - 1.36)	2 (1 – 3)
Bathing water status – beach visited most often	From ‘poor for 5 years’ to ‘sufficient’	39.38 (31.89 – 46.87)	-
	From ‘poor for 5 years’ to ‘good’	46.06 (36.96 – 55.16)	-
	From ‘poor for 5 years’ to ‘excellent’	84.76 (53.14 – 116.39)	-
Litter - 1% litter removed at beach visited most often		0.44 (0.25 – 0.62)	-

Base: Choice experiment analysis (1,013). 95% confidence intervals in parenthesis (Delta method).

As shown, the estimated WTP per household for improvements in the bathing water quality at the beach visited most often increases with higher status levels. The greatest value is attached to ensuring a bathing water meets ‘excellent’ status, with the WTP for the shift from ‘poor for 5 years’ to ‘excellent’ of approximately £85. The additional value from achieving other status levels is relatively marginal. In particular, the value for the shift from ‘poor for 5 years’ to ‘sufficient’ (approximately £39) is not statistically different from the value for the shift from ‘poor for 5 years’ to ‘good’( approximately £46), as is shown in the overlapping 95% confidence intervals in Figure A3-1. Likewise the value for a shift from ‘good’ to ‘excellent’ is not statistically different, however shifting from ‘poor’ to ‘excellent’ is.

These results indicate that the subtle differences in quality that are achieved by shifting from ‘sufficient’ to ‘good’ may not be of particular value to visitors. It is reasonable to assume that because visitors can swim at both levels, the other water quality improvements achieved from ‘sufficient’ to ‘good’ and the benefits from this may be less apparent. The results also show that there is a premium for a site achieving ‘excellent’ status, and may be due to the additional awards (e.g. blue flag) that can be acquired at this status.

Figure A3-1: Value of improvement in individual bathing water status

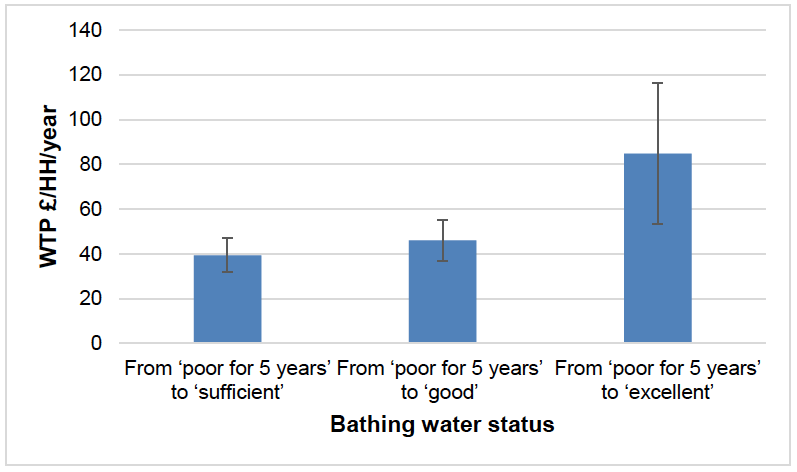
WTP for the number of Scottish beaches failing to meet water quality (1% reduction in bathing waters in Scotland failing) and WTP for one unit increase in litter removed (implies that 1% more beach litter is removed) are statistically significant, and are valued at £0.93 and,£0.44 per household per year respectively.

The total WTP per year presented in the final column of Table 6.3 is calculated as the WTP per household multiplied by the number of household in Scotland ( NRS, 2016). As shown, reducing the number of Scottish beaches failing by 1% is associated with a value of £2 million per year. This value can be presented as an annualised benefit over a specified time horizon for use in decision-making, for example within policy appraisal and/or for comparison against the costs of achieving the reduction in beaches failing within a cost benefit analysis. The WTP values for bathing water status and litter are ‘per beach’ values and can be aggreagated further based on a user population of a particular beach, but were not aggregated as part of this study.

A-3.3.6 Local economic impact model

The local economic impact modelling undertaken produces an overall estimate of GVA for each of the five surveyed sites. Whilst the GVA estimate is an aggregate figure stemming from all visits to a site, the analysis makes a further distinction between different visitor types. Visitors are broken down into: (i) local residents; (ii) day trippers; (iii) overnight visitors staying in the local area; and (iv) overnight visitors staying outside of the local area. The ‘local area’ relevant to the classification of overnight visitors is an area within a 5 miles radius of a bathing water. The size of the ‘local area’ is determined by the distribution of onsite survey data on respondents’ distance travelled to the site (i.e. the survey location).

With respect to overnight visitors (also referred to as ‘staying visitors’), the modelling attributes their entire stay to the bathing water at which they have been surveyed. Therefore, locally staying visitors have their entire length of stay and subsequent expenditure attributed to the locality and included in the economic impact to the site. This approach potentially over-estimates the economic impact of staying visitors as, typically, a proportion of visitors’ length of stay could be spent away from the local area (i.e. leakage). However, in the absence of data, visitors’ entire expenditure and length of stay are attributed to the local area. The rationale for this approach is that the coastal location is likely to be the main motivation behind visits. Therefore, in the event of a deterioration of the quality of a coastal location, the whole visit would be lost rather than a reduction in visitors’ length of stay. The approach also ensures that all sites are treated consistently by avoiding further site-level ad-hoc assumptions.

Estimated visitors to sites are combined with average spend per visitor per day to derive total visitor spend at sites per year. The breakdown of expenditure is based on data from the survey which have then been applied to the visitor number estimates for residents, day trippers and overnight visitors staying outside of the local area. Expenditure data have been applied to the total stay of overnight visitors staying in the local area in order to capture the whole of their stay in the area. Accommodation spend has only been applied to overnight visitors staying in the local area. The following points should also be noted:

• The expenditure figures represent the total spending at a site / coastal vicinity;
• Spend breakdowns are constrained to the most robust spend figures for all visitors;
• Original spend figures derived from survey data are only included where the sample size broken down by visitor type is greater than 30; and
• Gaps in the spend data due to small sample sizes (<30) at a site level are supplemented using regional variations of visitors types and periods compared to all expenditure which are then applied to the total spend figure at a site level.