Scottish Marine and Freshwater Science Vol 6 No 12: The demography of a phenotypically mixed Atlantic salmon (Salmo salar) population as discerned for an eastern Scottish river

Estimating Stock Recruitment Relationships

Relating stock and recruits

For each of the sub-stock decompositions, the data described above either provides directly, or allows one to infer, yearly time-series of both spawning stocks and their subsequent smolt outputs. To use these data as the basis of a stock-recruitment relation requires one to associate spawning stock in one year with recruitment (smolt output) at some later time - a process which is materially complicated by individual to individual variability in time taken to develop from ova to smolt.

The actual freshwater age distributions of cohorts of North Esk smolts going to sea is well established from large samples of smolt scales obtained from Kinnaber lade (for details see Todd et al. 2012). The smolt-age distribution at the North Esk (which is rather typical of east-coast Scottish fish (Bacon et al. 2011)) has changed slightly over the duration of our study period (Todd et al. 2012), and the annual age-stratified estimates ( i.e. including the trend, its annual fluctuations and any recording errors) were hence used here, with one simplification; to maximise data-points (by reducing data-loss from 'end-effects' ^[1] ) consequent on collating smolt contributions over four freshwater-emigrant age-classes, from S1s to S4s), the smolt-ages considered were amalgamated into S2's and S3's (S2'=S1+S2; S3'= S3+S4), ignoring the small average contributions of S1s and S4s (6.9% and 0.5% respectively).

To determine the total smolt output ( O _i,y) associated with the year y spawning stock for a particular sub-stock ( A _i,y), we define ψ _{d ,y} as the (sub-stock independent but calendar year dependent) proportion of the yearly smolt production ( p _i,y) which smolt in the d ^th year after ova deposition and thus see that

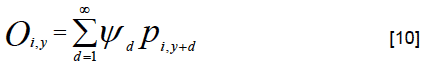
Bayesian estimation of a stochastic stock-recruitment relation

Standard Bayesian methods were used to determine the parameters of a stochastic representation of the spawning stock to smolt production relationship (Gurney et al. 2010 B); see the Discussion section for an explanation of why an ova-to-smolt relationship was not used instead. The expected relationship between stock ( A) and recruits ( O) is here represented by a conventional Beverton-Holt ( BH; Beverton and Holt, 1957) curve:

where O _max represents the maximum possible output (recruitment, here smolts) and H represents the spawner population needed to produce an expected recruitment of half the maximum. A further assumption made when setting up the model was that actual output values were Negative Binomially distributed around the expected value with a shape factor θ , which is approximately the inverse of the square of the coefficient of variation.

The maximum number of smolts produced per individual spawning fish was defined as:

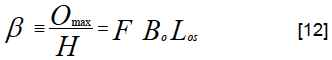
β can subsequently be decomposed into the product of the proportion of the spawning population which is female (F), the ova fecundity of the females (B _o) and the ova to smolt survival (L _os); see Supplementary Material, part I, for an illustration of how, and why this is useful.

As the life-history stages characterized by this adult-to-smolt stock recruitment relation are highly density-dependent, we used the prior-knowledge prescription of Gurney et al. (2010 B) to estimate initial informative `control priors' to define the prior parameter distribution from which the Markov-Chain Monte-Carlo process calculated a posterior distribution, representing the sum of knowledge provided by our new data and the prior. If the data do not show the saturation implied by the informative prior, then the estimated curve will be more saturated than if estimated with an uninformative prior, and the precision of the parameter estimates will be a little impaired (see Gurney et al. (2010 B) for details).

The resulting posterior distributions provide estimates of both the most plausible values for the model parameters ( O _max , H, θ ), the most probable expected stock recruitment relation ( ESR) and their credibility limitsAfter some experimentation, it was found that this process explored the posterior distribution rather efficiently, and that using a burn-in of 10 ⁴ iterations, followed by a MCMC sequence of 2 x 10 ⁴ iterations produced results which scarcely differed from those produced by an MCMC sequence a factor of 10 longer.

Changes in Fisheries Practice During the Study Period

A number of changes in fisheries practices occurred during the study period. Those which might be expected to generate changes in parameters reported in this paper include: reductions and subsequent phasing out of the distant-water fisheries in West Greenland (1971-1993) and the introduction (1978) and subsequent decline (ca. 1981-1992) of the Faroes fishery; change of the 'Morphie Dyke' net and coble fishery in the lower North Esk to a rod fishery in 1991; delayed start to the estuarine net-fishery season from mid-Feb to 1 ^st April in 2000, and to 1 ^st May in 2005; the gradual introduction of catch-and-release practices in the rod-fishery from the late 1990s (records kept since 1994) and, particularly, from 2001 onwards.

The first of these changes should alter the marine survival from smolt to pre-estuary adult ( PEA) for sub-stocks visiting the fishery areas, while the remaining three will change the proportion of pre-estuary adults who survive to spawn. The listed management changes should all produce enduring rather than transient parameter alterations, so our strategy for detecting such effects in the presence of strong year-to-year variability was to look for alterations in the decadally smoothed mean values of the parameter concerned.

Evaluation Criteria

The adult time-series data, both pre-fishery and spawner numbers, are contrasted between the single- and sub-stock-scenario results to assess whether the resulting time-trends differed. Those direct adult count data were particularly reliable. In contrast, enumeration of the smolt numbers derived from much less direct and more variable estimates. Comparison of smolt production was accordingly made as follows. An index of smolt productivity, per female per putative sub-stock, i (and thus independent of sub-stock size), was obtained from the appropriate sub-stock's SR curve by estimating β (eqn. 12). We then took ratios, for different pairs of the β _i sub-stocks, to assess whether one stock was relatively more productive than another ^[2] . However, as the sub-stocks differred in average female body-sizes, and fecundity is size dependent, those SR derived productivity ratios were then themselves divided by body-length predicted fecundity ratios for the same pair of sub-stocks. The procedure resulted in a sub-stock comparison index whose expectation is 1.00 if the SR derived ratio and size-expectation ratio are identical. The size-expectations were calculated from North Esk results reported in Bacon et al. (2012). Expectations are here presented for two ova-productivity criteria (total ova volume and total ova numbers), with the ova numbers being calculated both from the standard (historic, upland) equation and also with an egg-number adjustment for their actual upland/lowland breeding locale, where appropriate; the full calculations are explained and illustrated in Supplementary Material, part E.