Scottish Marine and Freshwater Science Vol 6 No 12: The demography of a phenotypically mixed Atlantic salmon (Salmo salar) population as discerned for an eastern Scottish river

Data Analysis

Density-dependent and Density-independent Life-cycle Segments

Many studies have demonstrated that the major density-dependent processes in the life-cycle of Atlantic salmon occur during the freshwater stages (eg Jonsson et al. 1998; Gurney et al. 2010) and that the demographic processes between emigration to sea as a smolt and return to the spawning grounds as an adult are essentially density-independent (eg Gurney et al. 2010).

In this analysis the density-dependent part of North Esk's salmon population life-cycle was regarded as starting with the return of adult spawners to their natal habitat and ending with emigration of their progeny to sea as smolts. For each distinct sub-stock, this part of the life-cycle was characterised by a separate stock recruitment relationship. The available information about the density-independent parts of the life-cycle was heavily concentrated in the segment between return to the estuary and spawning, so this segment of the life-cycle was treated separately from the segment between smolting and return to the estuary (hereafter referred to as `at sea').

The 'at-sea' portion of the Atlantic salmon life-cycle, while complex, shows no evidence of density-dependence. It is composed of fisheries mortality in both distant water (oceanic) and coastal commercial fisheries and predation mortality in both oceanic and coastal locations. For all of these there is little or no information that can be reliably attribute fish to the North Esk. At-sea survival is also affected by survival and growth processes that are complex, poorly understood and likely to vary in both space and time (eg Eriksson 1994; Friedland 2013; McGurk 1996; Salminen et al. 1995). This study required an objective approach to characterise the at-sea mortality of specific cohorts (hereafter smolt-year-classes) of sub-stocks (spent differing periods at-sea and having appreciably differing body sizes on return). As we could find no suitable quantitative data for Atlantic salmon that could be generalised to Scottish fish, we here adapted an allometric approach based on McGurk's (1996) results for Pacific salmonids.

The sizes, sea-ages and seasonal return times of Scottish Atlantic salmon vary within seasons and have varied over time (Bacon et al. 2009): by the 1970s the number of three sea-winter (3 SW) salmon at the North Esk (and on the eastern coast of Scotland more generally) had declined to near zero. The proportion of previous-spawners is also very low (1.7% on the Scotland east coast generally, Bacon et al. 2009) and only 0.9% for the North Esk. Consequently, the sea-age structure was simplified by treating the repeat-spawners and 3+ SW salmon as ' MSW' fish, but characterising their periods at sea as if they were 2 SW (hereafter 2 SW' ). Average periods at sea (assuming a median smolt emigration time of May for all smolts and a median monthly return time for each of the proposed sub-stocks based on their scale-read ages and counts) were used for each putative sub-stock, of 16, 22 and 28 months for grilse, early- and late2 SW' fish respectively, with associated mean sizes at return of 60, 72.5 and 80 cm fork-length respectively.

Estimating Sub-population Smolt Production and Sea-survival

To partition smolts among phenotypic stocks we denoted the number of individuals of sub-stock i returning to the river in year y by R _i,y, the total smolt production that year as P _y and defined an (unknown) quantity φ _i,y to represent the proportion of the year y smolt output who will, if they survive, return to the river as sub-stock i individuals. Finally we denoted the proportion of sub-stock i individuals going to sea as smolts in year y who will survive to form part of the pre-estuary population in year y + τ _i as S _i,y so that

As The φ _i.y (proportions i of the year y smolt production), must sum to one over all sub-stocks, for each year. Hence we know that for each and every year y

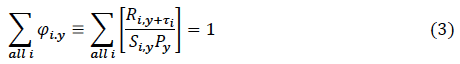
Equation (3) is little use, because it contains as many unknowns as there are sub-stocks. However, if, for each sub-stock i, we can relate each S _i,y to a single year-class-dependent constant, ε _y , so that

then equation (3) becomes

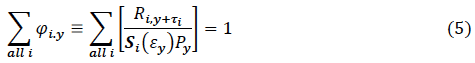
which, for each year in which total smolt output P _y and subsequent pre-estuary numbers {R _{i,y+τ i} } are known, can be solved for the single unknown ε _y . Although few variants of equation (5) have closed-form solutions, its general case is readily treated numerically (we used optimise from the R package, R Dev. Team, 2011).

Once we know ε _y, we can calculate the proportional survival from smolt to returner ( S _i,y) of sub-stock i individuals emigrating to sea in year y from equation (4) and the number ( P _i,y) of such individuals from,

The time-series of smolt to PEA survivals calculated from this process for any given sub-stock are related by a non-linear transformation defined by our assumption about S _i , to those for other sub-stocks whose smolts form part of the un-differentiated smolt-output observations.

Modelling Smolt to Pre-estuary Survival

One needs an explicit definition of the function S _i (ε _y ) to model smolt to pre-estuary survival. However, a number of plausible alternatives exist, given the paucity of data to test such models.

A simple formulation for smolt to pre-estuary survival, which we called the uniform risk-rate ( UR) model, assumes that all individuals (of whatever sub-stock) who emigrate in year y are subject to the same per-capita, per-unit-time mortality rate while at sea. In this formulation, if sub-stock i individuals spend m _i months at sea, then ε _y is the at-sea mortality rate for individuals emigrating in year y and set

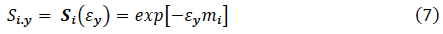
A potentially much more realistic formulation can be found in the work of McGurk (1996) who examined the marine-mortality of a number of species of Pacific salmon, and concluded that the marine survival ( s) of a species whose individuals go to sea at weight W _o and return to spawn at weight W _s can be well described by

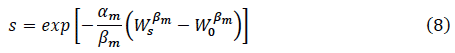
Although the values that McGurk obtained for his parameters α _m and β _m varied considerably between species, the form seemed highly robust, so we shall postulate that the allometry parameter (β _m ) remains constant over time for a given sub-stock, and identify the ratio (α _m / β _m ) with our sub-stock independent smolt-year parameter ε _y. Hence we write

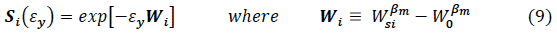
In this formulation, W _o represents the sub-stock independent smolt weight and W _si represents the spawning weight of sub-stock i individuals.

We examined two variants of this allometric model, which were differentiated by the value chosen for the allometry parameter β _m . Our default allometric mortality ( DAM) model used the value of β _m found by McGurk as most suitable for a composite dataset encompassing all five species of Pacific salmon covered by his study, namely β _m =-0.37. As an alternative quite extreme case, but which McGurk (1996) argued was also well supported, we examined a uniform survival ( US) model, in which all sub-stocks have the same smolt to pre-estuary survival ( N.B. this implies considerably different marine-mortality risk-rates), which we achieved by setting β _m = 0