Scottish technology ecosystem: review

Chapter 1 – Model for Scotland’s Technology Ecosystem

In this section, we describe Scotland’s Technology Ecosystem according to a model that will be used throughout the rest of this document and which sets the context in which all recommendations to support and improve the ecosystem will be made. We outline the basic structure of the model and then explore its dynamic aspects. This provides a foundation from which to later identify deficiencies in our ecosystem as it is currently operating and to propose remedies for those deficiencies.

What we mean by “Technology” and “Tech”

Before examining the model in detail, we’ll first define what we mean by a “tech business”, “tech start-up” etc. This is an important question because nowadays all businesses are “tech” businesses to some extent or other, in the sense that they are all at least tech-enabled. But, if we cast our definitional net too widely, it will be impossible to identify meaningful interventions that effectively benefit any particular sub-sector. Even within that category of businesses that can be described as technology-intensive, or “high-tech”, precise definition can be problematic.

Another complication arises from the question as to whether it is meaningful, in the context of this review, to segment businesses by domain; for example, Fintech, Greentech, Cybertech, Healthtech, Biotech etc.

We have chosen to address these definitional problems by focussing the review on start-ups and scale-ups that exhibit – or aspire to exhibit – certain attributes and characteristics common to successful tech start-ups internationally, regardless of the particular domain in which they operate. These attributes are:

• Develops a product or service with a high degree of software engineering required to develop it.
• Aspires to operate according to Internet Economy methodologies. We use this term to characterise a certain approach to product development and management. It is characterised by a strong focus on speed of iteration within a business context, on organisational agility at all levels of scale, on a relentless pursuit of product-market fit, on the application of modern growth engineering techniques such as the exploitation of compounding growth mechanisms, and on a very high degree of data-driven experimentation, to highlight just a few examples. Another short-hand term that could be applied to summarise these practices is The Silicon Valley Playbook.

This deliberately is not a rigorously bounded definition. There will be businesses that don’t completely overlap with the attributes described but which will benefit from the recommendations put forward in this review. Think of those attributes, therefore, more as a “centre of gravity” for how a business should operate to be considered a “tech start-up”. This matters because our global competition, such as those start-ups that are located in the Silicon Valley, operate on exactly these terms. They are Scotland’s competition. Our ecosystem must meet the standards of global best practice to be competitive. Therefore, the model presented below and the recommendations that flow from it, are designed to support businesses with this centre of gravity.

We are deliberately agnostic on business domain, preferring to focus instead on developing and supporting start-ups with the above attributes, independent of domain. To illustrate the reason for this decision, consider that Zoom, Slack, Tesla, Google and Pinterest, to name just a few examples, all operate in different domains but operate to the same Internet-Economy business practices and draw from the same talent pool.

This is not to say that focussing on supporting specific domains isn’t valuable as part of our wider industrial strategy, in terms of developing network clusters of expertise, etc. However, we argue that this should not be our underlying core strategy but is instead additive to it. It is a relatively simple matter to select domains of interest, but quite another to execute at a world-class level within them. Thus, this review focusses on the latter, while acknowledging the desirability of the former. We also note that it is unlikely that a highly prescriptive national domain-support strategy would have identified Skyscanner or FanDuel (two of Scotland’s most successful tech start-ups and then scale-ups) as worthy of support or attention, for example. Or that it would have identified, ahead of time, the emergence of the Games sector in the North-East. Therefore, our primary focus on this review is on levelling-up our general capability to produce world-class scalable tech companies, regardless of domain membership.

Finally, we note that the definition of a tech start-up used in this review also includes those born via the university spin-out route.

With that context in place, let’s now develop the ecosystem model on which the rest of this review will base its analysis and recommendations.

Ecosystem Model Overview

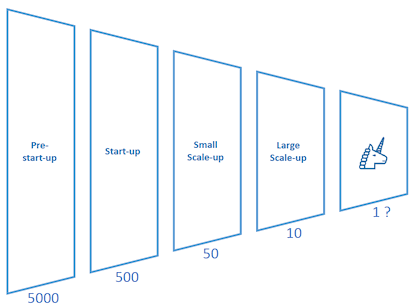
The technology ecosystem can be thought of as a funnel, as depicted below. We start, on the left-hand side of the diagram, with a relatively large number of potential founders considering starting a tech company, or in the very earliest stages of running a start-up, and we then proceed through various stages of scaling until companies reach “unicorn” size or larger^[1]. In other words, the eventual output that our model is optimising for is the rate of creation of successful, large-scale tech businesses. Of course, as we’ll see, this also results in the creation of many more tech businesses of other sizes along the way which, together, also create enormous value.

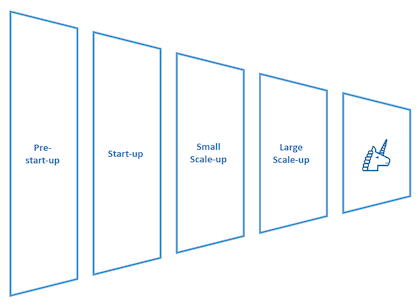
Naturally, the funnel narrows from left to right – not all start-ups become scale-ups and not all scale-ups become unicorns, nor should they. So, there’s a minimum narrowing rate of the funnel that it’s impossible to improve upon. But, in most ecosystems, the rate of narrowing is much faster in practice than this natural rate. This is certainly true of Scotland’s ecosystem. The difference between these two rates is the opportunity available to us.

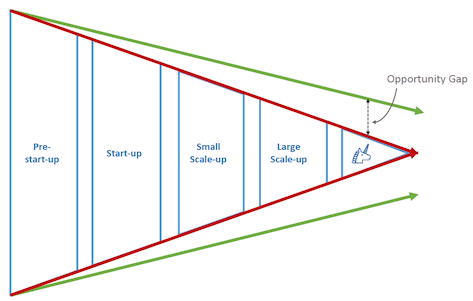
We assert that the difference in these two rates is due to deficiencies in the local ecosystem’s support environment for start-ups and scale-ups. One aim of this review is to make recommendations that close the gap between our current rate of funnel decay and the natural rate.

Let’s now explore some important dynamics associated with this model.

Importance of the early funnel stages

The technology industry is characterised by an astonishing rate of technological and market change. The consequences of this are that many once-successful companies later fail, while many more will fail on the way to scale. That’s one of the reasons why the early stages of the funnel are so foundationally important. If these stages are vibrant and well populated then, regardless of technological and market changes, the ecosystem is more likely to regularly produce larger-scale companies from their midst and replace those that have not maintained currency with markets and technology. Additionally, founders and employees from early-stage companies in the funnel that fail will take those hard-earned lessons to other start-ups, thereby strengthening them. The Silicon Valley is the archetypal example of these effects in operation.

This is what’s known as an antifragile ecosystem^[2] – stressors acting on the system actually make it stronger (c.f. a fragile ecosystem where stressors weaken or break it). It’s a highly desirable feature of our target ecosystem.

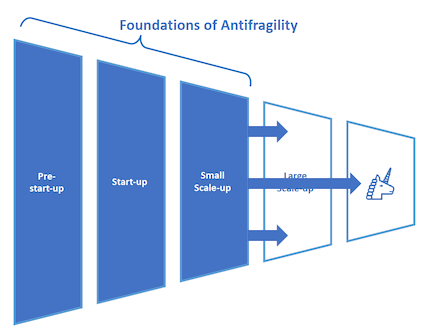
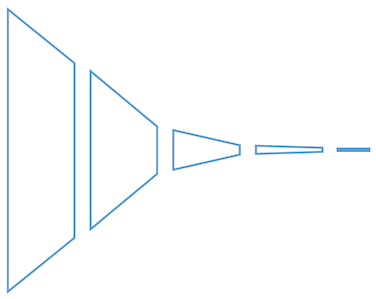
By contrast, consider the technology ecosystem in Scotland during the 1980s. Essentially, we skipped the early stages of the funnel and imported large-scale tech companies from abroad. The funnel therefore looked like this:

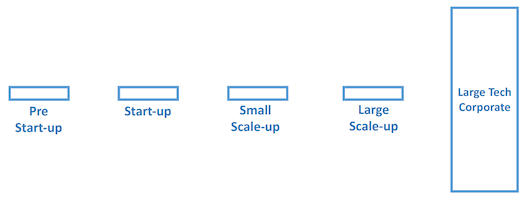
When the economic cycle turned over, and those companies left, the earlier stages of the ecosystem were practically non-existent, and couldn’t replace those lost jobs quickly. To be clear, it is welcome and desirable that our ecosystem includes large-scale external companies; they bring several benefits to the ecosystem, in terms of employment, engineering and management technique, and exposure to large-scale business practices, to name just a few. But the ecosystem must be healthy at all stages to be anti-fragile.

How many start-ups are needed to create one unicorn?

The other reason why the early funnel stages are so important returns us to the concept of the natural narrowing rate of the funnel. An interesting question to explore in this regard is: how many start-ups are needed to (eventually) create one unicorn?

The following figures are estimates but serve for illustration purposes: working backwards through the funnel from right to left, we probably need at least 10 large scale-ups, on average, for one unicorn to emerge from them. For each of those large scale-ups, we likely need at least five small-scale ups from which one large scale-up may emerge. Continuing from right to left, we find that, overall, we need approximately 500 start-ups to produce one unicorn, on average. This also illustrates one of the reasons why the concept of a minimum scale for our ecosystem is important. And it certainly indicates the size of the task before us.

Funnel Tipping Point

There are non-linearities in the model. If the number of start-ups reduces below a certain threshold level, the funnel collapses. The funnel then appears as below. In this state, there is an insufficient number of earlier-stage companies to fuel the emergence of larger scale-ups and unicorns.

Below this threshold point the following factors contribute to this funnel collapse:

• There just aren’t enough companies to create a sustained learning and experiential environment. This, in turn, means that there aren’t enough experienced employees emerging who know how to take a start-up to scale.
• The ecosystem is too small to attract outside talent. The risk is just too great that if a job doesn’t work out at a particular company for which an executive relocated her family from London, then there aren’t other companies to move to locally, and she has to return home. Few people will relocate their families in the first place, in these circumstances.
• The ecosystem doesn’t attract larger investors. VCs regard the ecosystem as too small to be worth exploration or they consider it unlikely that the ecosystem is capable of producing viable scale-ups. Consequently, they don’t invest or limit their investments. This in turn reduces the number of viable start-ups flowing through the funnel. The gap is partly filled by private individual investors and government, but their limited aggregate capital is unable to fuel the growth of businesses beyond the earliest stages of the funnel.

In a post tipping-point ecosystem, all of the above effects are reversed. If the number of high-quality, non-frivolous and well-run start-ups rises above a certain threshold, beneficial network-effects start to operate that accelerate the growth of businesses at all stages of the funnel.

Consider these examples: employees from successful later-stage companies typically start to take more senior positions in earlier-stage companies as a career-path opportunity. This significantly improves the experience level in those earlier stage businesses, which increases their likelihood of them being successful. This, in turn, creates a larger pool of recirculating talent. For example, there are already ex-employees of Skyscanner and Fan Duel working in multiple start-ups across Scotland.

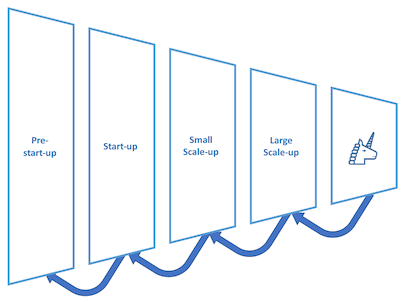
The second effect is that, above that tipping point, outside talent is attracted into the ecosystem (if a particular role at a business doesn’t work out then there are nearby companies that inbound executives can join without having to relocate back to their home city or country). This leads to the creation of both more start-ups and more successful ones at that. This in turn attracts more talent, and a virtuous cycle again establishes itself.

The third network effect is that investment firms start to pay greater attention to the ecosystem, and spend more time within it. This brings more money and expertise into the ecosystem, which leads to more and stronger businesses, which attracts more investors.

How do we know when an ecosystem has passed the tipping point? While it isn’t a simple matter to predict the precise number of businesses required to pass through the tipping point, it’s readily apparent through observation whether or not this has occurred.

For example, it is clear that Scotland’s ecosystem currently operates in the pre-tipping point state. The above network effects are not yet operating. Our over-arching strategy, therefore, must be to implement support and interventions that accelerate the ecosystem towards the tipping point. That support can then be tapered-down as the strengthening network effects described above start to develop.

It can be argued that Scotland’s ecosystem, certainly prior to the economic crisis brought about by COVID-19, was closer to this tipping point than at any time in its modern history. By the end of 2019 there were more start-ups (and more unicorns) in our ecosystem and more investment into those start-ups than ever before.

This presents us with an important opportunity, provided the appropriate interventions are made. When just below the tipping point, small interventions can have a dramatically accelerative effect on the ecosystem. There are multiple examples of such interventions – relatively simple actions that result in disproportionate benefit – contained in the recommendations section of this review.

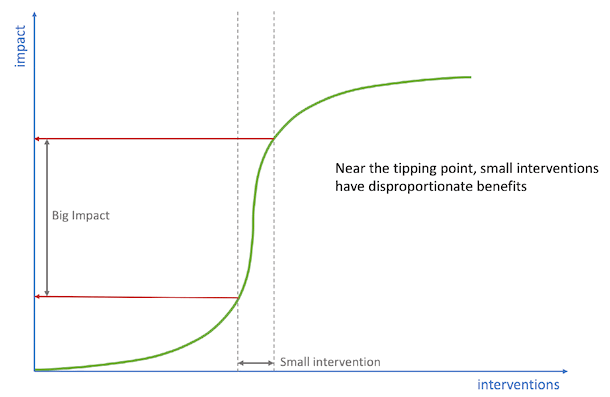
Global Versus Local Optimisation

A critical point regarding the model is that all interventions in the ecosystem should be assessed only with respect to the output of the overall global model, rather than with respect to localised areas within it.

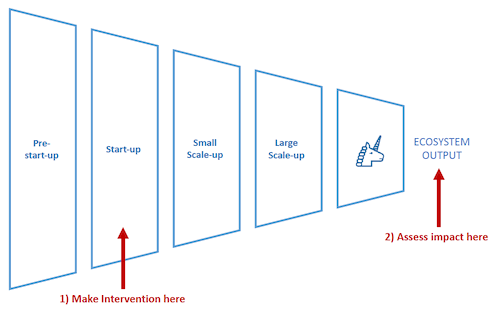
The importance of this point cannot be emphasised strongly enough. In this review, there are several actions recommended that certain stakeholders may find difficult to implement for local reasons^[3]. They will certainly run counter to existing, local KPIs in some cases. And because they do, absent our model and our understanding of this principle, they would be disregarded, to the detriment of our ecosystem.

But the impact of implementing such recommendations will have a profoundly positive effect on the output of the ecosystem as a whole. Similarly, some of our recommendations are “unglamorous” and when viewed in a context local to a given part of the ecosystem, they would be deemed unworthy of attention. But they conform to the optimisation principle that certain small interventions in a given part of a system can have a disproportionately positive impact upon the overall output of the system.

Because this principle is somewhat counter-intuitive, we will return to it when we present the specific recommendations of this review. In the meantime, it is very helpful to bear the principle in mind, as we shortly review the three categories of intervention types that can be applied across the ecosystem model.

Importance of a Portfolio Approach to Interventions

In general, interventions made in the very early stages of the ecosystem funnel, or in its dependent areas (discussed next) will have greater eventual impact overall than interventions made later in the funnel. This is because interventions made at the start of the funnel affect all later stages too. Conversely, investments made in later stages will yield a return sooner, because tangible start-up success only manifests from the middle of the ecosystem funnel onwards. Therefore, our interventions should constitute a balanced portfolio across the ecosystem’s stages, to bring about both early improvements and long-term high growth.

It might be tempting to only make interventions in later stages of the funnel because they yield an earlier return and because, as we shall see, they tend to be easier to make than earlier-stage interventions. But this would be a mistake. The effectiveness of later-stage interventions is permanently reduced if they are not made in conjunction with earlier-stage interventions. This is because earlier-stage interventions effectively create more “fuel” to power the beneficial effects of later-stage interventions.

Major factors influencing the performance of the ecosystem

The ecosystem model is dependent upon our combined approach in three categories. These are:

• Education
  Scope: across all stages of the ecosystem funnel, including, for example, start-up founder-team education in the Silicon Valley playbook.
• Infrastructure
  Scope: co-location and social infrastructure (the “market square”, in our parlance). Infrastructure refers both to physical and virtual versions, in each case.
• Funding
  Scope: includes public-funding and the stimulation of private funding capacity and capability. Covers investment and grant funding.

We will expand on these definitions in the analysis that follows shortly.

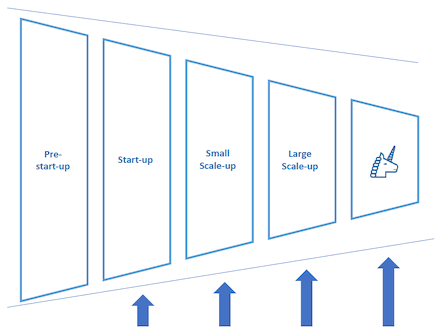
The overall ecosystem model can therefore be updated to reflect these dependencies as follows:

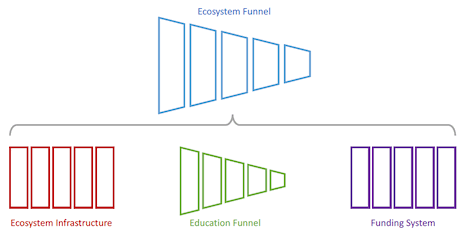
Our approach in this review is therefore to identify deficiencies of provision in each of these supporting categories that materially impact the sustainable output of the ecosystem funnel. We summarise this analysis in the following three sections of this review. Each section is structured as follows:

• We review the overall dynamics of each category.
• Deficiencies and areas for improvement are identified.
• A strategic framework for improvement is defined, which forms the basis of the later report recommendations.

In the final sections of this report, we then consolidate a set of specific recommendations intended to address the deficiencies identified.

Ranked, Relative Importance of the Factors

None of the above three areas can be omitted from our scope if we are to successfully accelerate our ecosystem towards and past its tipping point. All are important. But, in this review, we assign the greatest importance to recommendations in the Education category, followed by Infrastructure followed by Funding.

To some, this may appear to be exactly the wrong way around. After all, the argument goes, without funding, it’s impossible for our start-ups to reach maturity. But public seed investment funds already struggle to find enough credible candidate early-stage start-ups in which to invest. And, at the Series A stage^[4], external investors believe that the ecosystem produces too few well-run, non-frivolous start-ups and scale-ups to consider setting up a presence in Scotland or spending time here.

The funding will come to Scotland when the country regularly produces a sufficient number of credible candidates in which to invest. In other words, the virtuous network effects described earlier will become established as we near and then pass the ecosystem tipping point. To achieve that, we need to increase the average likelihood for success of our start-ups. And education – including in world-class, best practice start-up leadership and related techniques – is foundational to achieving that goal. Put simply, we need to educate our way to sufficient deal-flow to attract the interest of Series A funding institutions. Our ecosystem infrastructure is then the platform from which that education – both formal and informal – can be delivered.