Scottish Marine and Freshwater Science Volume 5 Number 2: A Protocol for Implementing the Interim Population Consequences of Disturbance (PCoD) Approach...

Appendix 2: Structure of the Interim PCoD Model

The interim PCoD approach uses the same stochastic population dynamic modelling framework as population viability analysis ( PVA) - see, for example, Morris & Doak (2002) - and we have adopted the terminology used by Morris & Doak in describing its details. PVAs are generally carried out to estimate the probability that a population will become extinct, or fall below some critical population size, over a defined time horizon. However, the same general approach can be used to model any series of population events where small numbers and uncertainty are expected to play a large role.

We divide each population that we model into 10 age or stage classes:

• pups or calves (depending on the species being modelled),
• one-year olds,
• two-year olds,
• etc., up to age eight,
• all animals aged nine years and above, combined into a single stage class.

Each of these classes is divided into six disturbance categories. First, we divide animals on the basis of whether or not they have experienced PTS. Within each of these two broad classes, we further divide animals into those that have experienced no disturbance, and those that have experienced 'significant' disturbance that is sufficient to affect their chances of survival or, in the case of adult females, giving birth. Finally, we divide animals in the significant disturbance classes into two categories depending on whether they have experienced 'moderate' or 'high' levels of disturbance. This results in the following six disturbance categories:

(1) Animals that experience PTS

• but no significant disturbance
• and 'moderate' levels of disturbance
• and 'high' levels of disturbance

(2) Animals that do not experience PTS

• and experience no significant disturbance
• but do experience 'moderate' levels of disturbance
• but do experience 'high' levels of disturbance

The criteria for assigning animals to each of these categories are described in the next section. Animals that experience disturbance in one year are reassigned to the relevant undisturbed age or stage class at the beginning of the next year. However, animals that experience PTS remain in one of the PTS categories throughout their simulated lives.

The six disturbance categories and 10 age/stage classes result in 60 age-disturbance combinations that are modelled as a 60-element vector using a Leslie matrix structure (Caswell 2001). The Leslie matrix provides information on the survival and fertility rates for each element and moves animals from one age/stage class to the next one at the end of the year. This is a birth-pulse model, which does not attempt to model changes in population size during the course of a year, and which assumes that all births occur at the start of the year. This has two implications: the start date for a year of simulation should coincide with the time at which most pups/calves are born, and changes in numbers within a year have to be modelled separately. We discuss the way we have dealt with the second implication in the next section. The first implication can be addressed by starting the year on 1 June for all the priority species except grey seals, which pup in October/November. The model is run using numbers of females only. The simulated population is scaled to the full population at the end of the simulations assuming a 50:50 sex ratio, except in the case of grey seals, whose population structure is believed to be strongly skewed towards females as a result of the high mortality suffered by male pups (Hall et al. 2001).

In the current implementation we model the dynamics of each population over a period of 24 years (equivalent to four of the six-year reporting cycles specified in Article 11 of the Habitats Directive).

Simulations are conducted using code written in the R statistical computing environment (R Development Core Team 2010).

Defining Vulnerable Sub-Populations and the Probabilities of Experiencing Disturbance and PTS

It is quite possible, and highly likely for large MUs, that only a proportion of the population within an MU will spend time in the region around a particular development where sound exposure levels are sufficiently high that they will cause a behavioural response. We have therefore included a capability within the protocol to specify the proportion (which can, of course, be 1.0 - i.e., all animals in the population are vulnerable) of the population that is vulnerable to disturbance from each development. We refer to this as a vulnerable sub-population of the population of animals within an MU. It is possible to specify that members of a particular vulnerable sub-population may be affected by more than one development. We assume that individuals who are not part of a vulnerable sub-population are never exposed to disturbance associated with any of the developments being modelled.

We simulate the likely exposure to disturbance of up to 1000 individuals from each vulnerable sub-population on each day of construction or operation. Each individual in a vulnerable sub-population is assumed to be equally likely to be disturbed on each day of construction or operation. The probability that it will be disturbed is calculated from the ratio of the number of animals expected to experience disturbance (as provided in the developers ES) to the size of the vulnerable sub-population from the appropriate MU. We assume that animals are only likely to experience PTS if they also experience disturbance. We therefore calculate the probability that a disturbed animal would experience PTS from the ratio of number of animals expected to experience PTS to the number expected to experience disturbance (as provided in the developer's ES).

Modelling Disturbance and PTS Within a Year

There is considerable evidence (Brandt et al., 2011; Teilmann & Carstensen, 2012) that harbour porpoises which have been disturbed by piling noise do not return to the area where piling occurred until some time (days to years) after piling ceases. We therefore assume that all of the priority species are likely to show this 'residual' effect of disturbance, and that 'residual disturbance' has the same negative effect on an individual's vital rates as that caused by the initial disturbance. Users of the protocol can specify how many days of residual disturbance are associated with each day of actual disturbance. Individuals exhibiting residual disturbance are assumed not to be vulnerable to PTS or any additional direct disturbance associated with construction or operation during the time they are experiencing this effect.

The basic model outlined above assumes that animals are at risk of PTS every time they enter the region where they may be disturbed by construction or operational noise. However, that risk is likely to be small, unless they are very close to the piling operation. It is therefore possible that they will avoid the immediate vicinity of operations after they have been disturbed once. We have therefore included a capability to model a scenario in which animals are only at risk of experiencing PTS on the first day they experience a sound exposure level sufficient to cause disturbance. The probability of experiencing PTS can be modelled in many ways; we have implemented only a few of these and we are not proposing that any one of them is definitive.

The within-year model estimates the potential exposure to disturbance for each individual in a vulnerable sub-population by conducting a random Bernoulli trial on each day that construction or operation is specified to take place using the probability of disturbance. If a simulated individual is scored as having experienced disturbance, a second Bernoulli trial is conducted using the probability that a disturbed animal will experience PTS. These within-year simulations therefore provide a day-by-day history of the exposure to sound levels sufficient to cause disturbance, 'residual' disturbance, and exposure to sound levels sufficient to cause PTS for every individual in each vulnerable sub-population. These histories are summarised to provide information on the total number of days of disturbance each individual experienced and whether or not it had suffered PTS. This information is then used to determine whether or not the simulated animals have experienced 'significant' disturbance and at what level using the criteria described below.

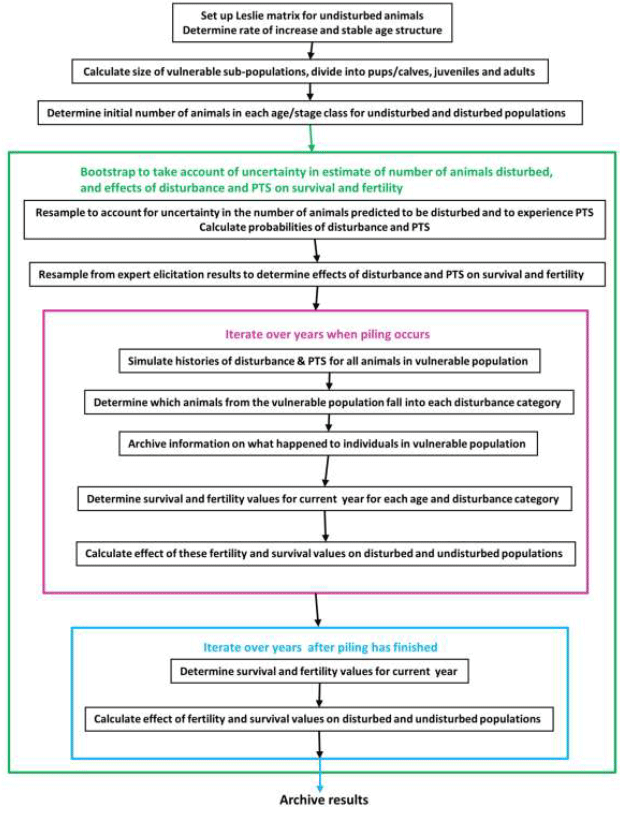
Figure A2.1 illustrates the process by which the number of animals in each age/stage class and disturbance category are calculated, and how the different sources of uncertainty are incorporated in the protocol.

Modelling Uncertainty

The interim PCoD protocol attempts to model many of the major sources of uncertainty involved in the calculation of the potential effects of an offshore renewable energy development on a population of marine mammals. These are:

1. Uncertainty about the size of the population in a particular MU;

2. Uncertainty about what proportion of that population will be vulnerable to the effects of a particular development;

3. Uncertainty in the predictions of the number of animals that will experience disturbance and PTS as a result of one day of construction or operation;

4. Uncertainty about predictions of the total number of days of disturbance an individual animal will experience during the course of construction of a development and of the total number of animals that will experience PTS;

5. Uncertainty about the effects of disturbance and PTS on vital rates;

6. The effects of demographic stochasticity and environmental variation.

Items 1 and 3 are related, because calculations of the number of animals predicted to experience disturbance and PTS depend, among other things, on the estimate of total population size that is used in the calculation. The population-level effects of these numbers are determined by uncertainty about what proportion of the population is actually exposed to the sources of disturbance on a particular day. This is not the same as the proportion of the total population that is potentially vulnerable to these effects, it is the proportion of that vulnerable population that is exposed to the disturbance on a given day. Uncertainty about estimates of the proportion of animals within a population that is likely to occur within "areas of interest for offshore development where estimates of abundance are of special conservation interest" (see Figure 2 of Paxman et al. 2012) identified by the SNCBs for the three cetacean priority species (harbour porpoise, bottlenose dolphin and minke whale) are being determined as part of the continuing analysis of data collected under the Joint Cetacean Protocol. In the North Sea, these "areas of interest" correspond roughly to the Round 3 zones for offshore wind farms. These uncertainty estimates can therefore be used to provide an indication of the uncertainty that is likely to be associated with estimates of the proportion of animals within a population that is likely to be exposed to disturbance associated with the construction of these wind farms. Preliminary estimates (Paxton, pers. comm.) have suggested that the 95% confidence limits on the proportion of animals within an "area of interest" are approximately ± 50% of the mean value. We have therefore tried to capture this uncertainty by multiplying the estimate of the number of animals predicted to experience disturbance on one day of construction or operation by this scalar:

exp(N(μ=0, σ=0.25 ))

This calculation does not, however, capture uncertainty in the estimate that could result from the use of different models for the propagation of the noise associated with construction or operation, or from the use of different ways of modelling the effects of hearing sensitivity at different frequencies, such as M-weighting (Southall et al., 2007) or dB _ht(Nedwell et al. 2007).

We could find no empirical basis for modelling uncertainty in item 2. Instead, we have presented the results of simulations using a number of different assumptions for this parameter.

Some of the uncertainty in item 4 was modelled by treating the exposure of each simulated animal to the noise associate with a particular development as a series of Bernoulli trials. This resulted in each simulated individual experiencing a different history of sound exposure. We could find no empirical basis for modelling uncertainty in how long the effects of disturbance may persist or in how prior exposure to construction noise may affect the risk of experiencing PTS. For simplicity, we have used only one model in the illustrative examples that we present in this report. It assumes that the effects of 1 day of actual disturbance persist for a further 2 days and that individuals are always at risk of experiencing PTS when they within the sound field generated by construction activities. However, we investigated the implications of these assumptions for selected scenarios.

Uncertainty in item 5 was modelled by drawing at random from statistical distributions derived from the results of the expert elicitation process. For each iteration of the model, the software selects a set of parameter values at random from these distributions. This is equivalent to soliciting the opinions of one 'virtual' expert for each iteration. These values determine the number of days of disturbance required to have a 'moderate' and 'high' effect on vital rates, the effects of this disturbance on those vital rates, and the effects of PTS on survival and fertility. At least 500 random draws were conducted for each development scenario.

Year to year variations in environmental conditions are likely to affect the survival and fertility rates for all individuals in a population. We modelled this environmental variation by asking experts "By how much do you think survival or fertility is likely to vary from year to year for populations of this species in northern European waters in the absence of disturbance?" and invited them to choose one of six percentage values ranging from 0% to 50%. Because many survival and fertility rates for marine mammals are close to 1.0 it is not possible for them to vary symmetrically around the mean from year to year. We therefore modelled environmental variation in each demographic rate using a beta distribution, whose mean corresponded to the baseline value used in the protocol and whose variance was adjusted so that the lower 99% confidence limit corresponded to the mean percentage value chosen by the experts. We assumed that variation in demographic rates was uncorrelated, both among age/stage classes and among years. Table A2.1 summarises the values we used.

Demographic stochasticity is caused by the fact that, even if survival and fertility rates are constant, the number of animals in a population that die and give birth will vary from year to year because of chance events. Demographic stochasticity has its greatest effect on the dynamics of relatively small populations, and we have incorporated it in models for all situations where the estimated population within an MU is less than 3000 individuals. One consequence of demographic stochasticity is that two otherwise identical populations that experience exactly the same sequence of environmental conditions will follow slightly different trajectories over time. As a result, it is possible for a 'lucky' population that experiences disturbance effects to increase, whereas an identical undisturbed but 'unlucky' population may decrease.

Table A2.1. Values used to describe environmental variation in demographic rates. Each value represents the lower 99% confidence limit for the rate, expressed as a percentage of the mean. We did not ask experts for their opinion about the level of environmental variation in calf and juvenile survival rates for minke whales, because these age classes are rarely observed in UK waters. However, we required these values to simulate the full dynamics of the population, and we therefore used the same values as those provided by the experts for bottlenose dolphins. *Grey seal pups were treated as juveniles ( i.e. independent of their mothers) as when they are pups ( i.e. dependent on their mothers) they do not enter the water to a great extent and therefore are not exposed to the same level of disturbance associated with offshore renewable energy developments as adults and juveniles.

Species	Pup/calf survival	Juvenile survival	Adult fertility
Harbour Seal	30%	30%	25%
Grey Seal	30%*	30%	20%
Bottlenose dolphin	25%	20%	30%
Harbour Porpoise	25%	30%	25%
Minke Whale	(25%)	(20%)	20%

Figure A2.1. The calculations involved in the interim PCoD protocol, illustrating how uncertainty is captured.

Appendix 2 - Literature Cited

Brandt, M., Diederichs, A, Betke, K., & Nehls, G. (2011). Responses of harbour porpoises to pile driving at the Horns Rev II offshore wind farm in the Danish North Sea. Marine Ecology Progress Series, 421, 205-216. doi:10.3354/meps08888

Caswell, H. (2001). Matrix Population Models: Construction, Analysis and Interpretation. 2 ^nd Ed. Sinauer Associates, Sunderland, MA.

Hall, A.J. , McConnell, B.J..& Barker, R.J. (2001). Factors affecting first-year survival in grey seals and their implications for life history strategy. Journal of Animal Ecology. 70, 138-149.

Morris, W.F. & Doak, D.F. (2002). Quantitative Conservation Biology. Sinauer Associates, Sunderland, MA.

Nedwell, J. R., Turnpenny, A. W. H., Lovell, J., Parvin, S. J., Workman, R., Spinks, J. A. ., & Howell, D. (2007). A validation of the dB ht as a measure of the behavioural and auditory effects of underwater noise. Subacoustech Report No. 534R1231.

Paxton, C. G. M., Mackenzie, M., & Rexstad, E. (2012). Revised Phase III Data Analysis of Joint Cetacean Protocol Data Resource. Report to Joint Nature Conservation Committee on Contract number C11-0207-0421. Centre for Research into Ecological and Environmental Modelling , University of St Andrews (pp. 170).

R Development Core Team. (2010). R: A language and environment for statistical computing. (Version 2.12).Vienna.: R Foundation for Statistical Computing. Retrieved from http://www.R-project.org/

Teilmann, J., & Carstensen, J. (2012). Negative long term effects on harbour porpoises from a large scale offshore wind farm in the Baltic-evidence of slow recovery. Environmental Research Letters, 7(4), 045101. doi:10.1088/1748-9326/7/4/045101