Offshore renewable developments - developing marine mammal dynamic energy budget models: report
A report detailing the Dynamic Energy Budget (DEB) frameworks and their potential for integration into the iPCoD framework for harbour seal, grey seal, bottlenose dolphin, and minke whale (building on an existing DEB model for harbour porpoise to help improve marine mammal assessments for offshore renewable developments.
This document is part of a collection
7 Bottlenose dolphin in the NE Atlantic DEB model
7.1 Model parameters
Table 7 shows the baseline parameter values used in the model. Details of how these values were derived are outlined below.
| Parameter names | Code name | Value | Description | Source |
|---|---|---|---|---|
| Resource density | ||||
| R | Rmean | 3.54 | Annual mean resource density | See text |
| abeta | a_beta | 23.65 | Shape parameters of beta distribution defining stochasticity in resource density | See text |
| bbeta | b_beta | 19.35 | See text | |
| amplitude | 0.1 | Parameter defining the amplitude of seasonal variation in resource density | See text | |
| offset | 0 days | Parameter determining when during the year Rmean has its maximum value | See text | |
| Timing of life history events | ||||
| min_age | min_age | 5 years | Minimum age for reproduction | |
| mean_birth day | mean_birthday | 15 July | Mean calving date for Moray Firth | Cheney et al. (2019) |
| TP | Tp | 365 days | Gestation period | Perrin & Reilly (1984) |
| TL | Tl | 1095 days | Age at weaning (duration of lactation) | See text |
| TR | Tr | 412 days | Age at which calf’s resource foraging efficiency is 50% | See text |
| max_age | max_age | 65 years | Maximum age | Wells & Scott (2018) |
| max_age_calf | 1075 days | Maximum modelled age of calf | ||
| Reserves | ||||
| ρ | rho | 0.34 | Target body condition for adults | See text |
| θF | Theta_F | 0.2 | Relative cost of maintaining reserves | Hin et al. (2019) |
| Growth | ||||
| L0 | L0 | 165.4 cm | Length at birth | B.Cheney (pers.comm.) |
| L∞ | Linf | 343.3 cm | Female maximum length | |
| b | b | -0.69545 | 5-parameter log-logistic dose-response curve developed by Finney (1979). | |
| ee | c | 0.1 | ||
| M | M | 5.38968 | ||
| ω1 | omega1 | (1- ρS )*10-5.03 kg/cm | Structural mass-length scaling constant | Lower 95% quantile from Hart et al. (2013) |
| ω2 | omega2 | 3.01 | Structural mass-length scaling exponent | |
| Energetic rates | ||||
| σM | Sigma_M | 4.5 | Field metabolic maintenance scalar | Field measurements fin winter from Bejarano et al. (2017) |
| σG | Sigma_G | 30 MJ/kg | Energetic cost per unit structural mass | Derived using the approach of Hin et al. (2019) |
| ε | epsi | 25.8 MJ/kg | Energy density of reserve tissue | Reilly et al. (1996) |
| ε- | epsi_minus | 23.2 MJ/kg | Catabolic efficiency of reserves conversion | |
| ε+ | epsi_plus | 35.5 MJ/kg | Anabolic efficiency of reserve conversion | |
| μs | mu_s | 0.2 | Starvation mortality scalar | Hin et al. (2019) |
| η | eta | 20 | Steepness of assimilation response | See text |
| ϒ | upsilon | 0.95 | Shape parameter for effect of age on resource foraging efficiency | See text |
| K | Kappa | 0.5 | Proportion of the daily assimilated energy allocated to growth | See text |
| Pregnancy | ||||
| fert_success | fert_success | 0.714 | Probability that implantation will occur | O’Brien & Robeck (2012) |
| Fneonate | F_neonate | 0.8* Fneonate kg | Threshold for pregnancy | See text |
| Lactation | ||||
| φL | phi_L | 5.4 | Lactation scalar | See text |
| σL | Sigma_L | 0.86 | Efficiency of conversion of mother’s reserves to calf tissue | Lockyer (1993) |
| TN | Tn | 183 days | Calf age at which female begins to reduce milk supply | See text |
| ξc | xi_c | 0.2 | Non-linearity in milk assimilation-calf age relation | See text |
| ξM | xi_m | 2 | Non-linearity in female body condition-milk provisioning relation | See text |
| Mortality | ||||
| foetal_mortality | foetal_mortality | 0.14 | Background foetal mortality | |
| α1 | alpha1 | 0.00039 | Coefficients of age-dependant mortality curve | Thomas et al. (2019) |
| α2 | alpha2 | 1.5 x 10-4 | ||
| β1 | beta1 | 0.005 | ||
| β2 | beta2 | 0.5 x 10-8 | ||
| ρS | rho_s | 0.1 | Starvation body condition threshold | See text |
| μs | mu_s | 0.2 | Starvation mortality scalar | See text |
| Disturbance | ||||
| Distdur | days.of.disturbance | Number of days on which disturbance occurs | See text for values | |
| Diststart | first_day | First day of disturbance period | See text for values | |
| Distend | Last_day | Last day of disturbance period | See text for values | |
| Disteffect | disturbance.effect | 0.25 | Reduction in resource density caused by disturbance | See text |
| AgeDist | age.affected | Age threshold defining which age class of simulated animals is affected by the disturbance | See text | |
7.1.1 Resources
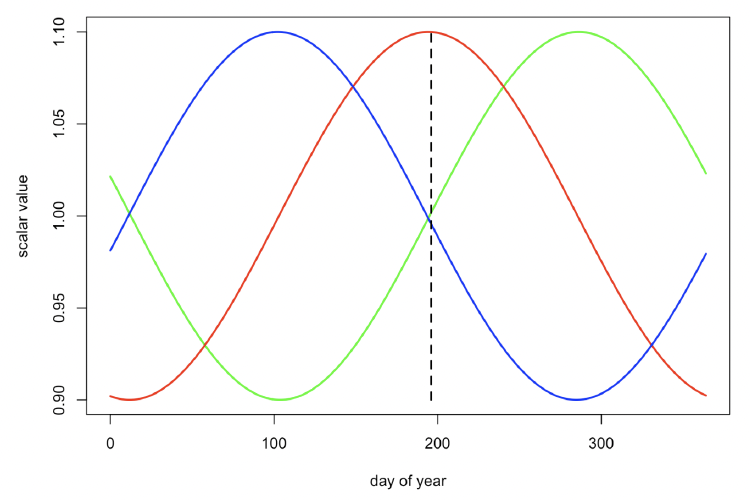
Resource density (Rmean) The strong seasonality in births observed in the Moray Firth bottlenose dolphin population (Cheney et al. 2018) suggests that resource density varies through the year and that ovulation is timed to optimize the lifetime reproductive success of females. We therefore experimented with the patterns of seasonal variation in Rmean shown in Figure 29 and identified which pattern resulted in the greatest reproductive success. Individual females had much higher reproductive success when Rmean varied according to the pattern illustrated in green in Figure 29, with a maximum value around 14 October (mid-way through the period when lactating females are provided all of their calves energy requirements), across a range of parameter values. We therefore used this pattern in all our simulations, although we investigated the effect of different values for the amplitude of the cycle.
In the original Hin et al. (2019) model, Rmean is assumed to be constant or to vary smoothly over the course of the year. However, in reality, the resource density encountered by an individual is likely to vary from day to day. This stochasticity in resource density can be modelled by multiplying Rmean for each day by a number drawn at random from a beta distribution with mean=1 and a 90% confidence interval of 0.5-1.5. Extreme values for this multiplier could be as low as 0.1 or as high as 2.4. We assumed that calves encountered the same resource density as their mothers on each day.
7.1.2 Timing of life history events
Cheney et al. (2018) detected a clear peak in first sightings of bottlenose dolphin calves in the Moray Firth between 1 June and 30 September. We therefore assumed that sexually mature female bottlenose dolphins ovulate every year, unless they have a young calf (in our simulations this is defined as a calf that is less than (TL-Tp) days old). For simplicity, we assumed that each female ovulates on her birthday, which was randomly chosen from a normal distribution with a mean equivalent to 15 July (the modal date on which calves in the Moray Firth were estimated to be born (see Figure 4 in Cheney et al. 2018) and a standard deviation of 10 days, which resulted in 99% of births occurring in a 50 day period centred on the mean birth day.
Gestation period (TP) This is generally considered to be 365 days (Perrin and Reilly 1984), although slightly longer periods (up to 395 days) have been recorded in captive animals (O'Brien and Robeck 2012). We used 365 days.
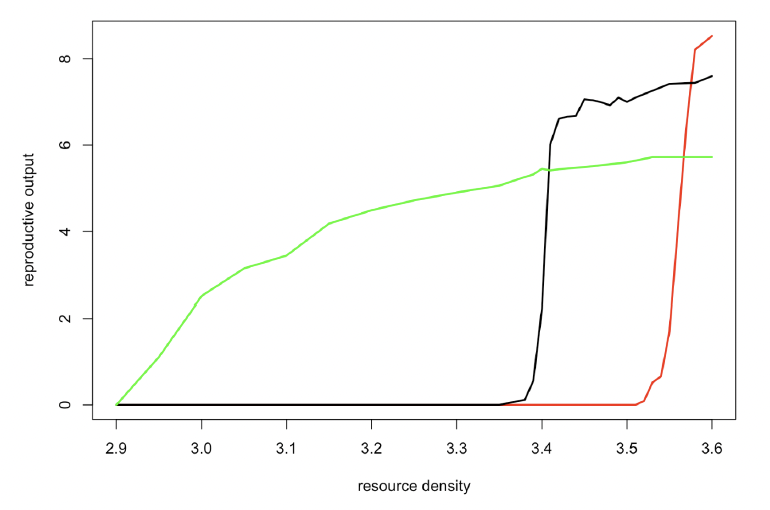
Lactation period/age at weaning (TL) Perrin and Reilly (1984) report an average age at weaning of 18-20 months. The oldest nursing calf presented in Table 7 in Perrin and Reilly (1984) was 38 months. A similar range (14-37 months) was recorded for captive animals by Kastelein et al. (2002). However, Grellier et al. (2003) reported that mother-calf pairs in the Moray Firth remain associated for 3 to “at least 8” years. We therefore investigated a range of values from 550 days (18 months) to 1095 days (3 years). Figure 30 shows that a 550 day lactation period maximizes lifetime reproductive success at high values of resource density (Rmean), but lifetime reproductive success declines sharply as Rmean is reduced because newly-weaned calves (which are relatively small) cannot maintain their weight, even if their body condition at weaning is close to ρ. At lower values of Rmean, a 730 day lactation period becomes optimal but reproductive success declines sharply as Rmean is reduced, because of low post-weaning survival. In both cases, calf survival remains high across the entire range of Rmean values. At even lower values of Rmean, a 1095 day lactation period becomes optimal, but in this case it is calf survival rather than post-weaning survival that decreases as Rmean is reduced. We conducted most simulations with a lactation duration of 1095 days because this allows a population to persist over a wide range of resource densities and the effects of changes in resource density on demographic rates are similar to those observed in the wild (i.e., a reduction in calf survival with decreasing prey availability or increasing population size).
7.1.3 Reserves and growth
Reserve threshold (ρ) Bottlenose dolphins have a relatively thin blubber layer (thoracic blubber thickness 12-18 mm, based on Figure 2 of Noren and Wells 2009), with an almost two-fold increase in estimated blubber mass between summer and winter for animals older than 2 years (Figure 3 in Noren and Wells 2009). This suggests that blubber’s main role in this species is to provide insulation rather than to act as an energy store.
An alternative measure of reserve size can be derived from the difference in mass of dolphins of the same length. In an extensive analysis of measurements from bottlenose dolphins in Sarasota Bay, Florida, Hart et al. (2013) fitted a set of equations for predicting mass from length; we used their upper 95% quantile relationship between length and mass to estimate the target body condition by assuming that the difference in mass between the estimates from this relationship and the calculated value of Sa at the same age represented reserve tissue. This gave a value of 0.34 for ρ.
Relative cost of maintaining reserves (ΘF) We were unable to find any published data that would allow a value specific to bottlenose dolphins to be calculated for this parameter. We, therefore, suggest using the value of 0.2 assumed by Hin et al. (2019).
Structural length and structural mass (L0, L∞, ω1, ω2, b, c , M) Most published growth curves for bottlenose dolphins (e.g., Stolen et al. 2002, Neuenhoff et al. 2011, Bejarano et al. 2017) are not appropriate for UK bottlenose dolphin populations because the maximum length obtained by UK animals is substantially greater than observed elsewhere. However, Cheney et al. (2018) fitted a version of Richard’s (1959) growth curve using the 5-parameter log-logistic dose-response curve developed by Finney (1979) to field measurements of known-age Moray Firth bottlenose dolphins using laser-photogrammetry, calibrated with data from stranded animals. This has the form:
La = L0 + (L∞ - L0)/[1 - eb(log(a) - c)]M
where La is length at age a (in years); L∞ is asymptotic length; is length at birth; b and c are free parameters that adjust the slope and inflection point of the curve; and M describes the position of the inflection point relative to the asymptote. The fitted values (B. Cheney, pers. comm.) were
L0 = 165.4 cm
L∞ = 343.3 cm
b = -0.695
c = - 2.303
M = 5.390
In order to estimate core body mass from length we used the results of an analysis by Hart et al. (2013) of the relationship between mass and length based on an extensive set of measurements from bottlenose dolphins in Sarasota Bay, Florida. They suggested that animals which fell outside the lower 95% quantile of their relationship could be identified as emaciated. The appropriate formula is:
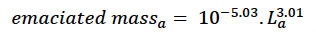
where mass is total mass at age a in days. This threshold corresponds closely with the mass:length ratio for emaciation suggested by Ridgway and Fenner (1982) based on data from 144 common bottlenose dolphins (from the Atlantic). We assumed that the body condition of these emaciated animals was at the threshold for starvation-related mortality (i.e., that reserves constituted ρs x 100% of their body mass). Thus:
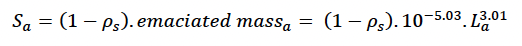
We assumed growth in foetal length was linear from conception to birth and used the same mass to length relationship as for adults.
Modelling growth (Κ) The model developed by Hin et al. (2019) assumes that growth in length and core mass continues unabated, regardless of energy intake. This is clearly not the case in many marine mammals. We, therefore, assumed that growth may be reduced if energy intake is less than the combined costs of metabolism, growth and reproductive activities (pregnancy and lactation). We modelled these circumstances using a modification of the kappa rule, which is a fundamental component of classic DEB models (Kooijman 2010). We assumed that an individual will allocate a proportion of the assimilated energy (It) it acquires on a particular day to growth (including growth of the foetus, because this is treated as part of the female’s core mass), up to a maximum of (1-Κ).It . If this amount of energy is less than the energy required for growth, the growth rate of the female and her foetus is reduced accordingly. The balance of the energy intake is allocated to metabolism. If this is insufficient to cover all of the costs of metabolism, reserves must be metabolised. Values of Κ < 0.5 indicate that growth is prioritised over metabolism. In the baseline calculation we used a value of 0.5, but the implications of other values should be explored. We also assumed that the costs of lactation are given absolute priority over those of growth. One consequence of this approach to modelling growth is that pregnant females who experience reduced energy intake may give birth to smaller calves than those that are able to meet their total energy requirements every day.
7.1.4 Energetic rates
Field metabolic maintenance scalar (σM) Bejarano et al. (2017) considered three different approaches for calculating the daily FMR of bottlenose dolphins, primarily based on data collected in Sarasota Bay, Florida. These were: estimates based on the amount of energy consumed per day as a proportion of body mass for captive animals; a simple multiple of the RMR estimated from the Kleiber equation (i.e. σM); and direct measurements of daily FMR (expressed in MJ/kg) from free-ranging animals in summer and winter. Direct measurements of FMR in summer were 40% more than those made in winter. Summer water temperatures in the shallow waters of Sarasota Bay (mean 29.7℃) (Noren and Wells 2009) are much higher than those likely to be encountered by bottlenose dolphins in UK waters, and so we believe that the winter values are more appropriate for these populations. These winter field measurements predicted a daily FMR that was 4.5 – 6x (depending on the value used for metabolic mass - MMa) the value derived from the Kleiber equation. We used values from this range, although most simulations were conducted with a value of 4.5.
Energetic cost per unit structural mass (σG) We were unable to find any published estimates of the energy density of lean bottlenose dolphin tissue. We, therefore, used the value of 30 MJ/kg that Hin et al. (2019) derived for pilot whales.
Catabolic and anabolic efficiency of reserve conversion (ε-, ε+,) In our simulations we assumed the same values for these parameters as those used for non-pups in the grey seal DEB. These are the same values as those used by Hin et al. (2019) for long-finned pilot whales.
Steepness of assimilation response (η) We were unable to find any data in the literature that could be used to set a feasible range for this parameter. We explored the implications of values between 5 and 25 and found that predicted changes in body weight and reproductive success were relatively insensitive to the value of this parameter. We, therefore, carried out most simulations with a value of 20.
Effect of age on resource foraging efficiency (Υ, TR): The majority of information on this parameter comes from studies of calves born in captivity. These animals are reported to begin feeding at age 6-18 months (Cockcroft and Ross 1990, Peddemors et al. 1992, Kastelein et al. 2002). Mann and Smuts (1999) record that bottlenose dolphin calves in the Shark Bay, Australia population that are >3 months old “frequently” chase small fish and trap them at the water surface (a behaviour they call “snack foraging”), with the earliest observation of this behaviour occurring at 3 weeks. The quantity of food consumed by the calves studied by Kastelein et al. (2002) increased linearly over time, and stabilised before they were weaned. The latter effect is probably an artefact of captivity, because fish will be more difficult to catch in the wild. We initially set γ = 3, and TR = 0.75*TL for TL = 550 and 730 days, and TR = 412 days when TL = 1095 days. This resulted in females providing 50% of their calves’ energy requirements at about the same time that the calf’s foraging efficiency was 0.5.
7.1.5 Pregnancy
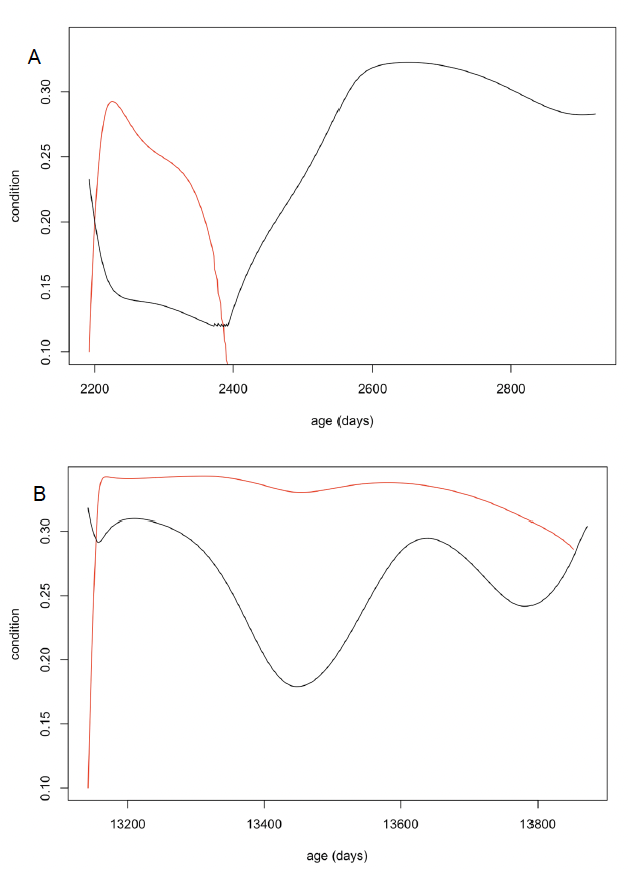
Pregnancy threshold (Fneonate): The pregnancy threshold determines when females become pregnant for the first time, and also how quickly they can become pregnant after the birth of a calf. Initially, we followed Hin et al. (2019) and assumed that a female can only become pregnant if her energy reserves at the time of ovulation are sufficient to cover the additional costs of foetal growth. However, the resulting levels of reserves at parturition were more than sufficient to allow all females to raise a calf successfully. We, therefore, reduced the pregnancy threshold to 0.8x Fneonate. Under this assumption, the calves of small females (i.e., those aged 6 to 10) suffered relatively high levels of starvation-related mortality (Figure 31), as observed by Cheney et al. (2018), whereas older females usually raised their calves successfully.
Probability that implantation will occur (fert_success) O’Brien & Robeck (2012) reported that only 71.4% of 119 documented reproductive cycles among captive bottlenose dolphins resulted in a conception, and we used this as the probability that a female whose body condition exceeded the pregnancy threshold would actually conceive in a particular year. Combined with the assumed values for foetal and calf mortality (see below), this resulted in an inter-birth interval of 2-6 years (c.f. 3.94 – 4.93 years; Arso Civil, et al 2017).
7.1.6 Lactation
Efficiency of conversion of mother's reserves to calf/pup tissue (σL): In the absence of any direct measurements of the relevant efficiencies for bottlenose dolphins, we used the value of 0.86 for long-finned pilot whales from Hin et al. (2019).
Effect of calf/pup age on milk assimilation (ξC, TN): Most data on these parameters comes from captive animals. Most of the lactating females studied by Kastelein et al. (2002) dramatically increased their food intake shortly after parturition, and then slowly decreased it (although food intake remained above the maintenance level until calves were weaned). In contrast, the food intake levels of the four captive, lactating females studied by Reddy et al. (1994) remained at the same high level for 18 months. Milk assimilation in the DEB model is affected by both the calf’s age and its body condition. As a result, calves that begin foraging early are predicted to demand less milk from their mothers than those that have not begun to forage. Thus, predicted milk assimilation may begin to decline before the calf is TC days old. We experimented with values of TN around 6 months and ξC = 0.2 (i.e., an almost linear decline in milk assimilation after age TN).
Effect of female body condition on milk provisioning (ξM) The relatively high mortality of young calves observed by Cheney et al. (2019), and the known longevity of bottlenose dolphins (e.g., Wells & Scott 2018 report that females in Sarasota Bay can live to more than 67 years) suggest that females may be reluctant to compromise their own survival by continuing to provide milk to their calves when their own body condition is low. We, therefore, used relatively low values of this parameter, in the range 2-3.
Lactation scalar (ΦL) We calculated the total costs of calf growth and calf metabolism up to the age of 6 months (the period during which females are assumed to be providing 100% of their calf’s energy needs) and assumed that the calf’s body condition was close to ρ throughout this period. This gave a value of 5.4 for ΦL . This resulted in the daily energy requirements of a lactating female in the first 6 months of lactation being 55-65% (depending on the female’s age) higher than a non-lactating female of the same age. This is very similar to the range of values used by Bejarano et al. (2017).
7.1.7 Mortality
Age-dependent mortality rate We followed the approach used by Hin et al. (2019) and estimated changes in the probability of survival with age using the approach developed by Barlow & Boveng (1991). The following function describing the variation in daily survival with age:
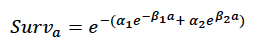
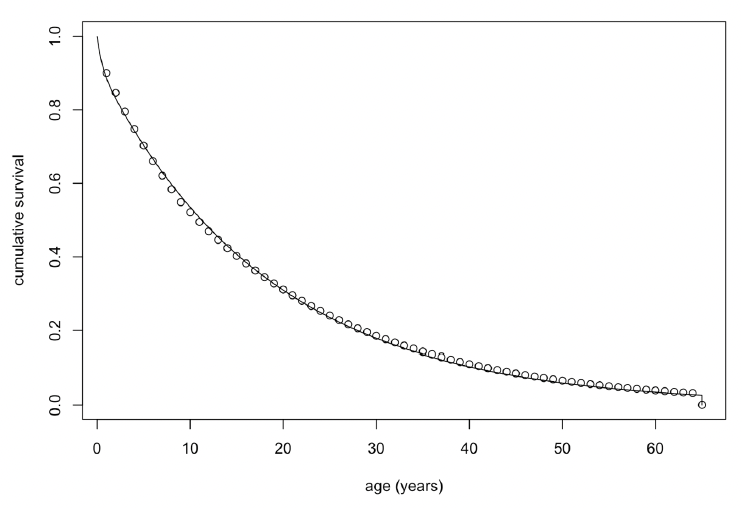
where a is age in days, was fitted to the annual age-specific survival rates for bottlenose dolphin survival rates recommended by Sinclair et al. (2020) for the Moray Firth population. Figure 32 shows the resulting relationship between age and cumulative survival, with
α1 = 0.00039
β1 = 0.005
α2 = 0.15x10-3
β2 = 0.5 x 10-8
and a maximum age of 65 years (as in Wells & Scott 2018). The life expectancy of each simulated female was calculated by choosing a random number between 0 and 1 and determining the age in days at which cumulative survival equalled this value.
Foetal mortality O’Brien & Robeck (2012) reported that 85.9% of 85 documented pregnancy among captive bottlenose dolphins resulted in a live birth. We, therefore, assumed that the background foetal mortality (i.e., mortality not related to the mother’s condition) over the entire duration of the pregnancy was 14%.
Starvation body condition threshold (ρs) As noted above, we were unable to find any empirical information on ρs. Instead, Sa is back-calculated from the mass-length relationship for emaciated animals and the assumed value for ρs. We investigated the implications of a range of values centred on ρs = 0.1.
Starvation-induced mortality rate (μs) No empirical information that could provide a species-specific value of this parameter for bottlenose dolphins is available. As a starting point for exploratory modelling, we used the value of 0.2 proposed by Hin et al. (2019).
7.2 Model results – pattern-oriented modelling
Using the default parameter values in Table 7, in particular a lactation duration of 1095 days, and a resource density of 3.2 results in a population growth rate of 0.99 (i.e., a 1% decline in abundance per year). Annual calf survival is 0.41 and the median inter-calf interval is 3.3 years (range 2-6 years). The highest population growth rate that can be achieved with this lactation duration is 1.018 (an annual increase in abundance of approximately 2%), identical to the mean growth rate presented in Table 4 of Sinclair et al. (2020). Annual calf survival is 0.72 and the median inter-calf interval is 3.8 years (range 2-10 years). These demographic characteristics closely match those reported by Cheney et al. (2018) and Arso Civil (2018).
7.3 Simulating the effect of disturbance
We simulated the effects of different numbers of days of disturbance within a single year on the vital rates of 1,000 females using the default parameter values shown in Table 7. Disturbance was simulated by reducing resource density by a proportion Disteffect on the days on which disturbance was predicted to occur. This has the effect of reducing assimilated energy by the same amount.
The condition of calves and lactating females is predicted to be at its lowest level in the first 8-12 months of lactation, as resource density increases from its lowest value in the annual cycle (Figure 33). This corresponds to the period from April – mid-July, and it seems likely that any disturbance at this time could affect both calf and adult survival. In addition, this is the time when females are building up reserves in advance of ovulation and a reduction in body condition could result in failure to implant.
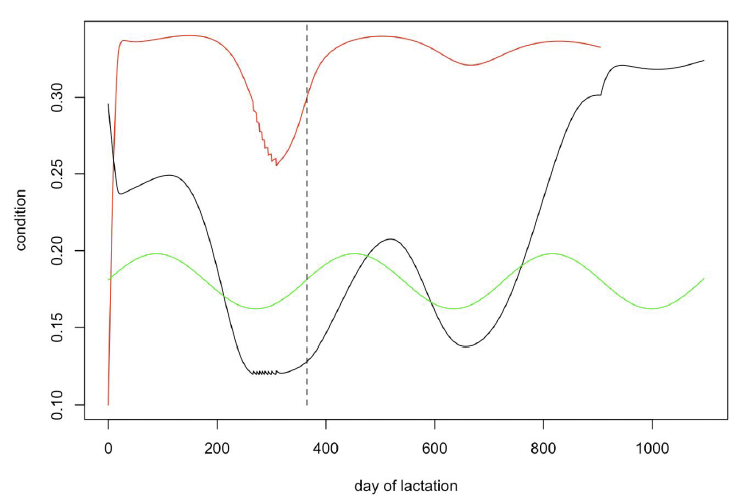
We therefore compared the effects of disturbance in three 4-month periods: May-August, September – December and January – April for young (7 years old) and mature (36 years old) females.
7.3.1 Disturbance between 1 May and 31 August
Disturbance that reduced foraging success by 25% during this period had no significant effect on any vital rate for mature or young females. Figure 34 shows the variations in calf survival from the start of the disturbance period to weaning with the number of days of disturbance.
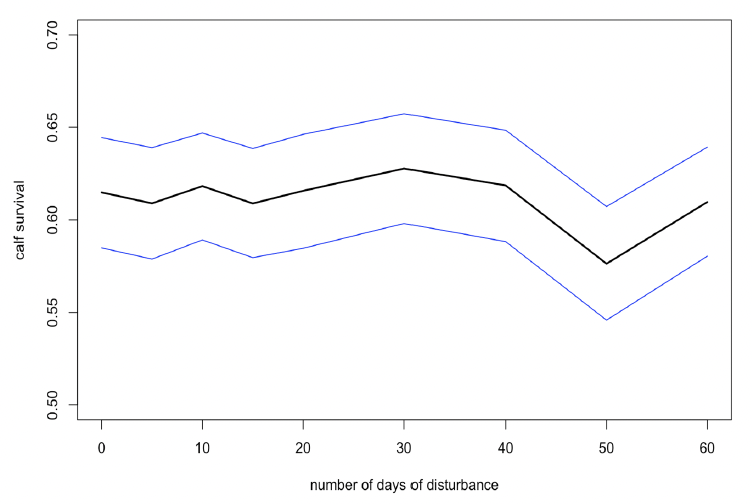
7.3.2 Disturbance between 1 September and 31 December
Disturbance that reduced foraging success by 25% during this period had no significant effect on any vital rate for mature or young females.
7.3.3 Disturbance between 1 January and 30 April
Disturbance that reduced foraging success by 25% during this period had no significant effect on any vital rate for mature or young females.
Contact
Email: ScotMER@gov.scot
There is a problem
Thanks for your feedback