Offshore renewable developments - developing marine mammal dynamic energy budget models: report
A report detailing the Dynamic Energy Budget (DEB) frameworks and their potential for integration into the iPCoD framework for harbour seal, grey seal, bottlenose dolphin, and minke whale (building on an existing DEB model for harbour porpoise to help improve marine mammal assessments for offshore renewable developments.
This document is part of a collection
4 Overview, design and details of DEB models for iPCoD
Below we present a generic description of the DEB models used in this report following the ODD protocol (Grimm et al. 2020), which was developed for describing agent-based models. The sub-models developed for each species are described in later sections.
4.1 Purpose and patterns
The purpose of the models is to explore the link between disturbance and population vital rates for five UK species of marine mammal (harbour porpoise, bottlenose dolphin, harbour seal, grey seal and minke whale), particularly in the context of offshore renewable developments. The models use the same approach as a previously published dynamic energy budget model for harbour porpoise (Harwood et al. 2020). The approach is based on first principles and explicitly accounts for the ways in which the energy budget of each individual varies, depending on its age, size, life history stage, and the environment it encounters (i.e., resource availability). Table 1 provides an overview of the variables considered in the models.
| Variable | Code | Unit | Description |
|---|---|---|---|
| For all individuals | |||
| a | age | days | Age |
| L | L | cm | Structural length |
| S | Sa | kg | Structural (core) mass |
| F | F | kg | Reserve mass |
| W | W | kg | Total body mass (S + F) |
| GR | kg/day | Daily growth rate (derived from S) | |
| ρ | rho | - | Relative body condition (F/W) |
| life_expectancy | days | Life expectancy derived from cumulative survival curve | |
| I | Ir | MJ/day | Assimilated energy |
| CM | Cm | MJ/day | Field metabolic costs |
| For pregnant or lactating females and their offspring | |||
| life history stage | - | - | One of four: resting, pregnant, lactating and pregnant & lactating |
| Fneonate | F_preg, skipping_point | kg | Threshold for starting or continuing pregnancy |
| Sfoetus | S_foetus | kg | Foetus size |
| GRfoetus | GR_foetus | kg/day | Growth rate of foetus |
| IMC | Im_C | MJ/day | Calf/pup assimilated energy from milk |
| IC | Ir_C | MJ/day | Calf/pup assimilated energy from prey |
| CL | CLact | MJ/day | Daily cost of lactation |
| CMC | Cm_C | MJ/day | Field metabolic costs for calf/pup |
To evaluate if the model simulations appear to be realistic, model outputs were compared to published and grey empirical datasets using the pattern-oriented modelling approach: seasonal changes in body condition, weight and assimilated energy of females and their offspring; calf/pup survival; and birth rate (proportion of reproductively mature females giving birth each year).
4.2 Entities, state variables, and scales
The model is a non-spatially explicit and is composed of one kind of entity: individuals of the modelled species. It follows individual females from an initial age (age_day1) until their death, the time of which is determined at the beginning of each simulation. Their offspring are followed from embryonic implantation up to age_day1 (described further see Table 2). The model proceeds in discrete time steps of 1 day, and each year consists of 365 days.
Individuals are characterised by the following state variable: age, length, structural (core) mass, reserve mass, and energy assimilation. These vary over time depending on an individual’s life history stage and the resource densities it encounters.
Females can be in one of four life history stages: ‘resting’ (i.e., neither pregnant nor lactating, this includes the juvenile period from weaning to first conception); ‘pregnant (but not lactating)’; ‘lactating (but not pregnant)’; and ‘lactating & pregnant’.
4.3 Process overview and scheduling
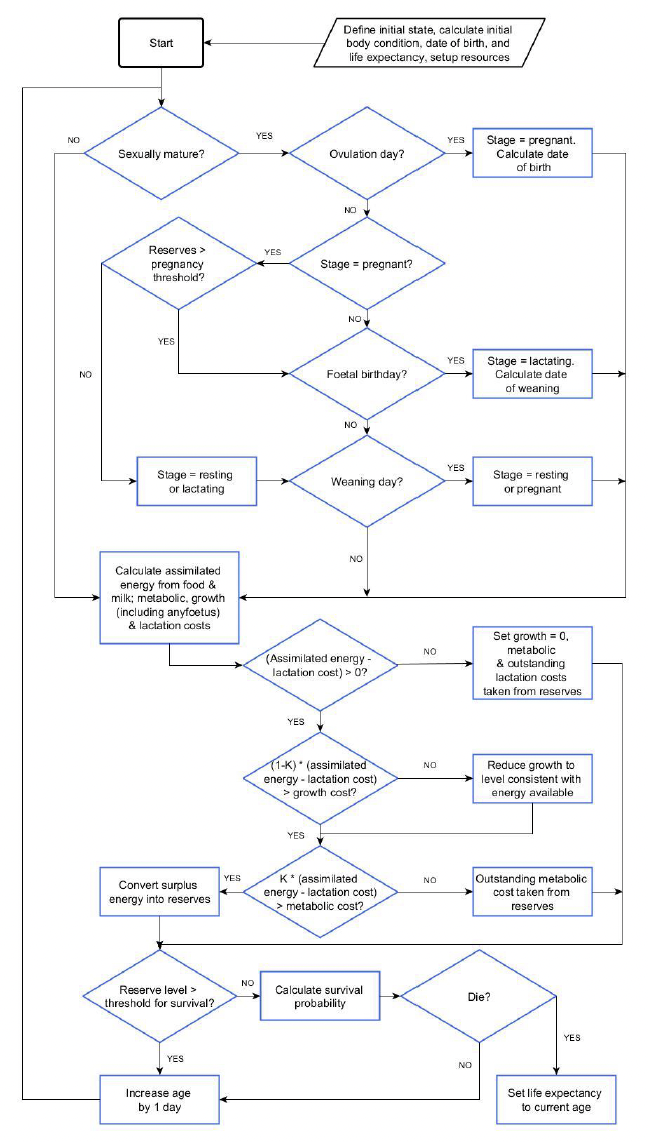
Figure 1 provides a flow chart outlining the model processes. We describe it further below. An individual’s assimilated energy varies with resource density, its body condition, structural mass and life history stage. Pregnancy begins on the day on which the embryo implants, which is determined by the day of the year on which the simulated individual was born. Foetal mass is included in maternal structural mass for the calculation of metabolic and growth costs. At any point in the pregnancy (the “decision day”,–see - Section 4.4.12), a female can abort the foetus if her reserves are too low. A calf/pup depends entirely on milk provided by its mother until a specified day of lactation (TN,–see - Section 4.4.12). Calf/pup demand for milk depends on its body condition and age. The amount of milk provided by the female depends not only on calf/pup demand but also on her body condition. Females abandon lactation if their relative body condition is close to the starvation threshold. At a specified point during the lactation period, the calf/pup starts foraging on its own and its foraging efficiency increases with age. Grey seal and harbour seal pups fast for a period after weaning, and their foraging efficiency is set to zero during this time.
If assimilated energy on a particular day exceeds the combined costs of metabolism, growth and reproduction, the surplus energy is converted to reserves tissue. Otherwise, individual females give priority to lactation. If lactation costs can be met from assimilated energy, a predefined proportion of the remaining assimilated energy is assigned to growth (including growth of the foetus if any). If this is less than the energy required for growth, the growth rate of the female and her foetus is reduced accordingly. The remaining balance of the energy intake is allocated to metabolism. Any unfulfilled energetic costs of lactation and metabolism are met by catabolism of reserve tissue. If the relative body condition of an individual falls below the starvation threshold (ρS - Section 4.4.12), they have an increased chance of death.
4.4 Design concepts
4.4.1 Basic principles
This model follows the approach developed by (Hin et al. 2010) for long-finned pilot whales, which uses the basic principles of DEB theory (Kooijman 2010). The model tracks the way in which individual female marine mammals assimilate energy over the course of their lives from age_day1 to death, and how this energy is allocated to field metabolism, growth, foetal development and lactation. If assimilated energy on a particular day exceeds the energy required for these activities, the surplus energy is stored in a reserve compartment (De Roos et al. 2009, Kooijman 2010)(De Roos et al., 2009; Kooijman, 2010), primarily – but not exclusively - as fat tissue around internal organs and as blubber. If energy expenditure exceeds energy assimilation, the balance is provided by catabolizing tissue from this reserve compartment. The model also tracks these energy fluxes up to age_day1 for every calf/pup that a female produces.
4.4.2 Emergence
Although individual life-history traits such as growth, non-resource driven survivorship, and maturation time are imposed, others emerge from rules of metabolic organization and are driven by the influence of seasonal differences in resource density and energy balance.
The use of a maximum probability for successful fertilization/implantation above a specified age imposes a cap on the annual birth rate. However, the actual number of pups/calves born and the actual age at first reproduction emerge from the current physiological state (body condition) of females. Age-related and seasonal fluctuations in body condition emerge from variations in the resource density experienced by individuals and seasonal changes in energy demand. Body condition then influences the individual’s probability of reproducing or dying. In this way, it is possible to use the lifetime reproductive output of each simulated female to examine the population consequences of different conditions (including a changing environment and/or the effects of disturbance).
4.4.3 Objectives
Animals attempt to maximize their fitness by allocating available energy to different life history processes in order of necessity. If processes necessary to survival are not covered by energy intake, stored energy will be used to cover them. As storage levels decrease, the animal has an increasing probability of dying.
4.4.4 Prediction
Females can predict whether they can successfully continue with pregnancy using proxies of their current body condition.
4.4.5 Sensing
Individuals can sense their storage levels and make decisions specific to their current body condition and life history stage, e.g., abort foetus or use energy converted from stores.
4.4.6 Interaction
The only interactions between individuals in the model are between mother and offspring. The foetus and calf/pup are linked to their mother via energy and mass transfer.
4.4.7 Stochasticity
The following processes can be stochastic: life expectancy of females, their foetuses and pups/calves; successful fertilization/implantation; dates relating to reproduction (e.g., calving/pupping date); deaths due to starvation (see Section 4.4.19 for further details); and the resource density that an individual encounters on a particular day.
4.4.8 Collectives
Collective behaviour is not modelled.
4.4.9 Observation
The values of all state variables for each individual are recorded daily. For model output corroboration, the following variables and follow-up calculations were used: length, structural mass, reserves and body condition, assimilated energy, cause of death, proportion of adult females breeding each year, calf/pup survival till age1 (reproductive success), inter‑birth intervals, and population growth rate.
4.4.10 Initialization
The model is initialised by creating a number of individuals defined by the user (sim_number), all of which have the same initial age (age_day1) and body condition ρstart (Table 2). Initial body condition is determined iteratively from the mean condition of simulated calves/pups at age_day1. Initial reserve level (Fstart) is then calculated as:
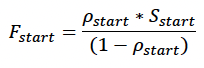
where Sstart is the female’s structural mass at age_day1 derived from the growth curve.
| Species | ρstart | Initial age |
|---|---|---|
| Harbour seal | 0.20 | 1 year |
| Grey seal | 0.22 | 1 year |
| Bottlenose dolphin | 0.2 | 3 years |
| Minke whale | 0.28 | 1 year |
Life expectancy of each individual at age_day1 is determined by sampling from a cumulative survival curve.
4.4.11 Input data
The time series of resource densities that will be encountered by an individual during its lifetime is created at the beginning of each simulation.
4.4.12 Submodels
The original model is cast as a set of differential equations (Table 1 in Hin et al. (2019)), which we have converted to difference equations. Throughout, we use the parameter symbols and names from Table 1 and Supplementary Information 1 (S1) in Hin et al. (2019).
| Variable, parameter | Code | Units | Description |
|---|---|---|---|
| Resource density | |||
| R | Rmean | Annual mean resource density | |
| abeta | a_beta | - | Shape parameters of beta distribution defining stochasticity in resource density |
| bbeta | b_beta | - | |
| amplitude | - | Parameter defining the amplitude of seasonal variation in resource density | |
| offset | - | Parameter determining when during the year Rmean has its maximum value | |
| Timing of life history events | |||
| min_age | min_age | years | Minimum age for reproduction |
| mean_birthday | mean_birthday | Mean date on which calves/pups are born | |
| TP | Tp | days | Gestation period |
| TL | Tl | days | Age at weaning (duration of lactation) |
| TR | Tr | days | Age at which calf’s resource foraging efficiency is 50% |
| max_age | max_age | years | Maximum age |
| max_age_calf | days | Maximum modelled age of calf/pup | |
| moult_duration | moult_duration | days | Duration of moult (seals only) |
| Reserves | |||
| ρ | rho | – | Target body condition for adults |
| ρc | rho_C | – | Target body condition for calves/pups |
| θF | Theta_F | Relative cost of maintaining reserves | |
| Growth | |||
| L0 | L0 | cm | Length at birth |
| L∞ | Linf | cm | Female maximum length |
| k | K | 1/days | Von Bertalanffy growth function: growth rate parameter |
| X0 | x0 | days | Von Bertalanffy growth function: length at age zero |
| ω1 | omega1 | kg/cm | Structural mass-length scaling constant |
| ω2 | omega2 | – | Structural mass-length scaling exponent |
| Energetic rates | |||
| σM | Sigma_M | – | Field metabolic maintenance scalar |
| σG | Sigma_G | MJ/kg | Energetic cost per unit structural mass |
| ε | epsi | MJ/kg | Energy density of reserve tissue |
| ε- | epsi_minus | MJ/kg | Catabolic efficiency of reserve conversion |
| ε+ | epsi_plus | MJ/kg | Anabolic efficiency of reserve conversion |
| ε+pups | epsi_plus_pups | MJ/kg | Anabolic efficiency of reserve conversion for pups |
| η | eta | – | Steepness of assimilation response |
| ϒ | upsilon | – | Shape parameter for effect of age on resource foraging efficiency |
| K | Kappa | – | Proportion of the daily assimilated energy allocated to growth |
| moult_reduction | – | Reduction in resource assimilation during moult (seals only) | |
| moult_duration | – | Duration of the moult period (seals onlu) | |
| Pregnancy | |||
| fert_success | fert_success | Probability that implantation will occur | |
| decision_day | decision_day | days of gestation | Day of pregnancy when female decides whether or not to continue |
| Fneonate | F_preg | kg | Reserve threshold for continuing pregnancy (cetaceans) |
| Lactation | |||
| φL | phi_L | – | Lactation scalar |
| σL | Sigma_L | – | Efficiency of conversion of mother’s reserves to calf/pup tissue |
| TN | Tn | days | Calf/pup age at which female begins to reduce milk supply |
| ξc | xi_c | Non-linearity in milk assimilation-calf age relation | |
| lact_feed | days | Day of lactation when female starts foraging (harbour seals only) | |
| R_prop_lactation | – | Proportion of time female spends foraging during lactation (harbour seals only) | |
| ξM | xi_m | – | Non-linearity in female body condition-milk provisioning relation |
| pw_fast | days | Duration of calf/pup’s post-weaning fast (seals only) | |
| Mortality | |||
| foetal_mortality | foetal_mortality | Background foetal mortality rate | |
| α1 | alpha1 | – | Coefficients of age-dependant mortality curve |
| α2 | alpha2 | – | |
| β1 | beta1 | – | |
| β2 | beta2 | – | |
| ρS | rho_s | – | Starvation body condition threshold |
| μs | mu_s | – | Starvation mortality scalar |
| Disturbance | |||
| Distdur | days.of.disturbance | days | Number of days on which disturbance occurs |
| Diststart | first_day | day of year | First day of disturbance period |
| Distend | Last_day | day of year | Last day of disturbance period |
| Disteffect | disturbance.effect | - | Reduction in resource density caused by disturbance |
| AgeDist | age.affected | years | Age class that will be affected by the disturbance |
4.4.13 Resource
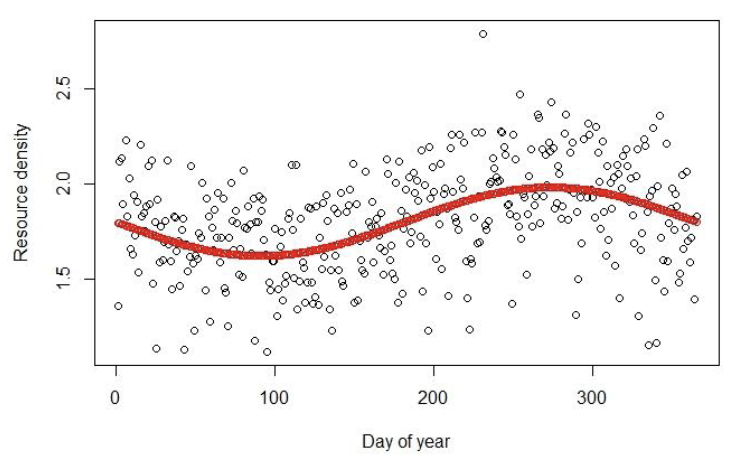
Resource density (R) To avoid having to account for differences among prey in energy density, catchability, and digestibility, and differences among individuals in their ability to assimilate energy, the model of Hin et al. (2019) characterises the resources on which a species feeds in terms of the amount of assimilated energy they can provide to a female. Although it would be virtually impossible to measure resource density defined in this way, R provides a useful quantitative index of environmental quality, with high resource density indicating high quality environments, and low resource density associated with poor environments. Seasonal variation in R is modelled using a sine function, following Hin et al. (2019).
R is the most important determinant of lifetime reproductive success (the number of female offspring raised to age_day1 in a female’s lifetime). It is therefore possible to choose an appropriate value for R based on what is known about the status of the population being modelled. For example, if the population is stable, R can be tuned so that lifetime reproductive success is 1.0.
Resource density can be deterministic or stochastic. In the latter case, R for each day is multiplied by a random number drawn from beta distribution with mean 1. An example showing the differences between fixed and stochastic R is given in Figure 2.
4.4.14 Timing of life history events
Gestation period (TP) This is usually estimated from a combination of estimates of foetal growth rate and mean length at birth, using the assumption that foetal growth in length is approximately linear (Perrin and Reilly 1984).
Lactation period/age at weaning (TL) Perrin and Reilly (1984) provide a review of the methods used to determine lactation period and age at weaning. These include estimates of the ratio of lactating to pregnant animals in a sample of mature females, estimates of the age of the largest calf observed associating with a female, stomach content analysis, and behavioural observations.
4.4.15 Reserves and growth
Reserve thresholds (ρ, ρs) In the Hin et al. (2019) model the rate of energy assimilation on a particular day is affected by an individual’s current body condition (ρt) relative to the target body condition (ρ). It is tempting to simply set ρ to the maximum recorded blubber: total body mass ratio for a particular species. However, captive harbour porpoises show strong seasonal variations in blubber thickness and total mass (Lockyer et al. 2003, Kastelein et al. 2019), which are closely correlated with water temperature and probably reflect a requirement for less insulation in summer. This suggests that in some species ρ may vary seasonally and that blubber mass cannot always be equated with reserve mass.
Relative cost of maintaining reserves (ΘF) According to DEB theory, reserve mass does not require any maintenance (i.e., ΘF = 0). However, the large lipid reserves maintained by most marine mammal species probably do incur additional costs in terms of drag and buoyancy. Hin et al. (2019) set ΘF to 0.2 in order to account for these costs.
Structural length and structural mass (K,L0, L∞, ω1, ω2, k, xo,) Most marine mammal DEB models have used a von Bertalanffy growth curve to describe changes in L0 with age, and then converted length to mass using a simple power function (e.g., Sa = ω1.Laω2). However, there is no requirement to use this approach, and any empirically derived relationship between weight and age can be used in the model.
4.4.16 Energetic rates
Field metabolic maintenance scalar (σM) The Hin et al. (2019) model assumed that an individual’s Field Metabolic Rate (FMR) is a simple multiple σM of the Resting Metabolic Rate (RMR) predicted by the Kleiber (1975) relationship (i.e., K.Mt0.75, where K = 0.294 MJ/kg/day). Estimates of σM can be obtained from respirometry studies of captive animals (e.g., Sparling et al. 2006, Worthy and Lavigne 1987), or they may simply be assumed. For example, Hin et al. (2019) used a value of 0.75 for σM.K based on the assumption that the FMR for pilot whales is 2.5x their RMR (Lockyer, 1993).
Energetic cost per unit structural mass (σG) This is the amount of energy required to produce 1 kg of tissue (i.e., the energetic content of the new tissue and the energetic overheads required to produce it). Hin et al. (2019) obtained an indirect estimate of σG = 30 MJ/kg from Brody’s (1968) formula for the heat of gestation and Lockyer’s (1993, 2007) estimate of the energy density of pilot whale calf tissue. However, direct measurements of this cost can also be obtained from captive animals (e.g., Noren et al. 2014 for Pacific walrus).
Catabolic efficiency of reserve conversion (ε-) This is the amount of energy produced by metabolising 1 kg of reserve tissue. It can be calculated from measurements of the changes in mass of fasting animals and estimates of their metabolic requirements during that fast (Bennett et al. 2007, Muelbert and Bowen 1993).
Anabolic efficiency of reserve conversion (ε+) This is the amount of energy required to produce 1 kg of reserve tissue. Since anabolism is likely to be less efficient than catabolism, Hin et al. (2019) used a value for ε+ that was ~40% higher than ε-. However, it may be possible to estimate this parameter from measurements of the amount of additional food consumed by captive animals that have experienced fasting. For example, Kastelein (2019) report that fasted, captive harbour porpoises recovered their original body weight within 2 days when they were offered twice the normal amount of food on those days. Estimates of the actual amount of additional energy consumed by these animals could be used to calculate ε+.
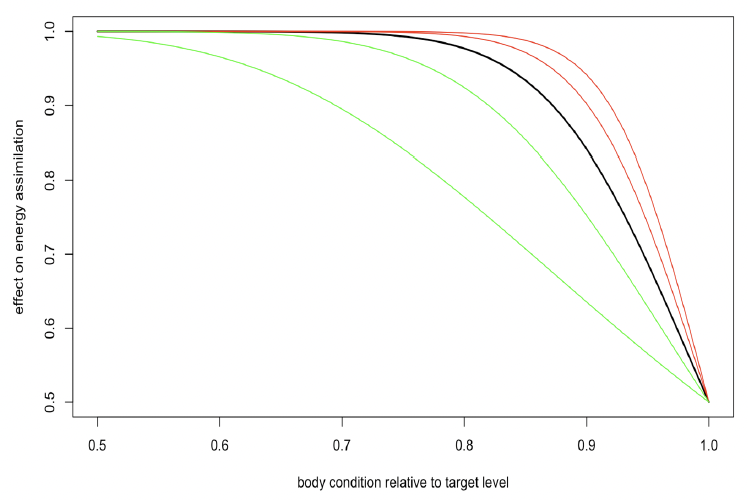
Steepness of assimilation response (η) The amount of assimilated energy obtained from feeding each day depends on the resource density, the structural size of the animal to the power 2/3 following Kooijman (2010), and the individual’s body condition (ρt). Individuals are assumed to assimilate energy at half of the maximum possible rate when their body condition is at the target body condition (ρ) and to increase their energy assimilation progressively if their body condition is reduced below the target value. This relationship also allows animals to compensate for the effect of lost foraging opportunities on their body condition by increasing energy assimilation on subsequent days, provided sufficient resources are available. Energy assimilation (It) on day t is described by:
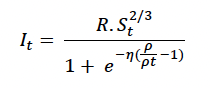
Figure 3 shows the effect of body condition relative to the target value ( and η on energy assimilation with η ranging from 5 to 25. The value of 15 used by Hin et al. (2019) is shown in bold. With higher values of η, energy assimilation is close to its maximum level over a wide range of value for ρt. Lower values of η result in a wider range of variation in energy assimilation with ρt. Information on how quickly fasting individuals that are in good condition recover the weight lost during the fast (e.g., Kastelein et al. 2019) could provide guidance as to a suitable value for η.
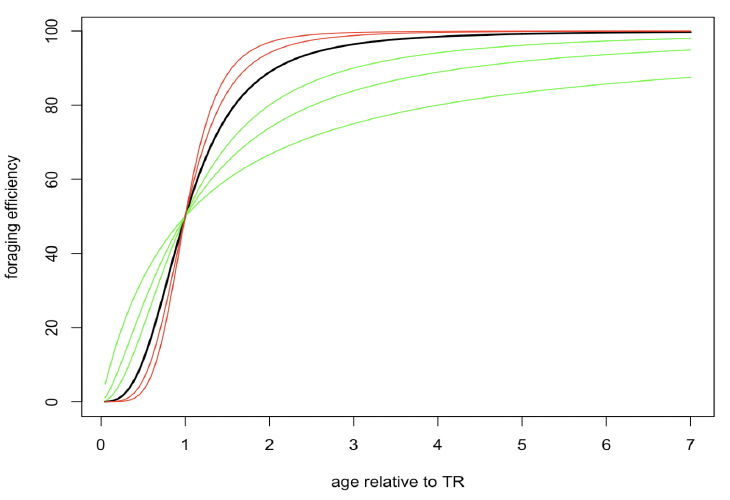
Effect of age on resource foraging efficiency (Υ, TR, pw_fast): These parameters take account of the fact that newly-weaned pups/calves will not be 100% efficient at foraging and that, for species with long lactation periods, calves may begin feeding during lactation. In addition, harbour and grey seal pups undertake a post-weaning fast, whose duration is set by the parameter pw_fast. The shape of the feeding efficiency relationship is controlled by TR, the age at which a calf/pup achieves a foraging efficiency that is 50% of an adult, and a shape parameter (γ) that determines how rapidly foraging efficiency approaches 100%. Figure 4 shows the effects of different values of γ on the shape of the function determining foraging efficiency. The value of γ = 3 used by Hin et al. (2019) is shown in bold. As an example, if TR is 1 year, the function predicts that 100% foraging efficiency would be achieved by age 5. Lower values of γ result in higher ages for 100% efficiency and higher values of γ result in lower ages for 100% efficiency. Although it may be possible to determine when pups/calves begin feeding independently from an examination of stomach contents (e.g., Figure 3 in Muelbert and Bowen 1993), direct estimation of these parameters is unlikely to be feasible. However, it will affect post-weaning survival and age at first reproduction. Independent information on current values for these demographic characteristics can therefore provide insights into the feasible range for this parameter.
4.4.17 Pregnancy
Pregnancy threshold (Fneonate, decision_day, skipping_point) The Hin et al. (2019) model assumes that females can only become pregnant when the size of their reserves exceeds Fneonate. They used a value equivalent to the energetic costs of foetal growth and development plus the amount of reserves needed to avoid the onset of starvation for pilot whales, but other formulations have been used (e.g., for beaked whales New et al. 2013). This effectively sets a minimum value for the age at first conception, because the absolute size of a female’s reserves is determined by Sa and young females are too small to build up sufficient reserves, even if their foraging efficiency has attained its maximum level. Estimates of age at first conception are available from many marine mammal populations and these can be compared with predictions from the DEB model to provide a “reality check” on the appropriateness of the value chosen for Fneonate.
Smout et al. (2019) documented a relationship between a female grey seal’s total mass at the end of lactation and the likelihood of giving birth in the following breeding season. The threshold mass that resulted in a 0.5 probability of giving birth was lower if prey abundance was greater than average in the subsequent year. Given that females do not increase their body mass from the end of lactation until implantation (Boyd 1984), this implies that in grey seals the decision to give birth to a pup is made some time during pregnancy, rather than at implantation. However, the exact time at which females should make this decision is not entirely obvious, and the model allows the user to define when this decision is made (decision_day). Further details are provided in the section on the grey seal model.
4.4.18 Lactation
Efficiency of conversion of mother's reserves to calf/pup tissue (σL) This parameter combines the efficiency with which a female converts ingested or reserve energy to milk and the assimilation efficiency of the calf/pup. Lockyer (1993) assumed that efficiency of milk assimilation is 95% and that the efficiency of milk production in the mammary gland is 90%. Combining these estimates yields a value of 0.86, which was used by Hin et al. (2019) and may also be useful for other cetacean species. Direct estimation of this parameter should be possible from studies of energy transfer in lactating pinnipeds (e.g., Costa et al. 1986, Lang et al. 2011). For example, Figure 3 in Costa et al. (1986) implies that conversion efficiency in northern elephant seals is close to 100%. However, it is not possible to calculate a precise value for σL from the results presented in this and other pinniped studies.
Effect of calf/pup age on milk assimilation (TC , ξC) Hin et al. (2019) proposed that females will provide all their calf’s energy demands until the calf is TC days old, and after this they will gradually reduce the amount of energy they supply according to the formula:
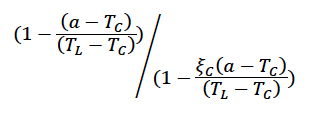
Where a is calf age and TL is age at weaning. Figure 5 shows the effect of the value of ξC on the shape of this relationship. For capital breeding species, such as many pinnipeds, which provide almost all of their pup’s energy demands up until the age at weaning, TC should be close to TL and ξC will be close to 1. Species, such as bottlenose dolphins, with an extended period of maternal care will have relatively small values of TC and ξC.
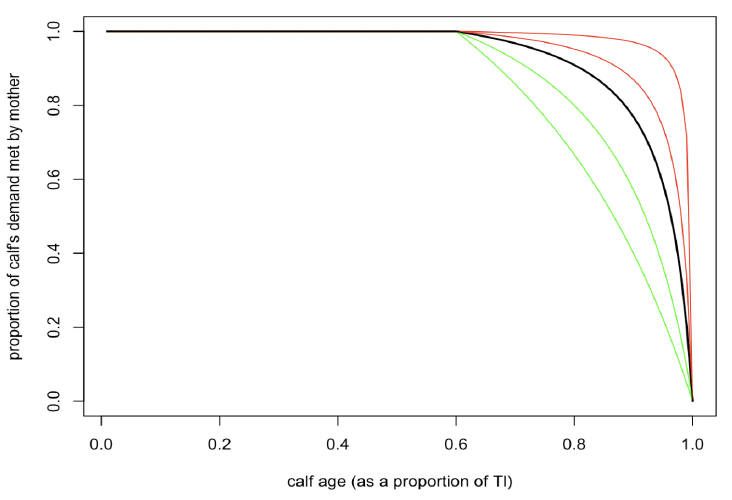
Effect of female body condition on milk provisioning (ξM) Hin et al. (2019) assumed that females will reduce the amount of milk they provide to their calf as their own body condition declines. They used the function:
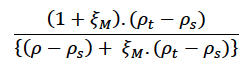
to predict this reduction, where ρt is the female’s body condition on day t, and ξM is described as the “non-linearity in female body condition-milk provisioning relation”. Figure 6 shows how the shape of this relationship varies, depending on the value of ξM. Lower values of ξM represent a more conservative strategy, with females reducing the amount of milk they supply by 50% if their body condition falls below 60% of ρ if ξM = 0.5. Larger values reflect a strategy that is more “generous” to the calf/pup. For example, if ξM = 10, body condition must be reduced close to ρs before milk supply is reduced by 50%.
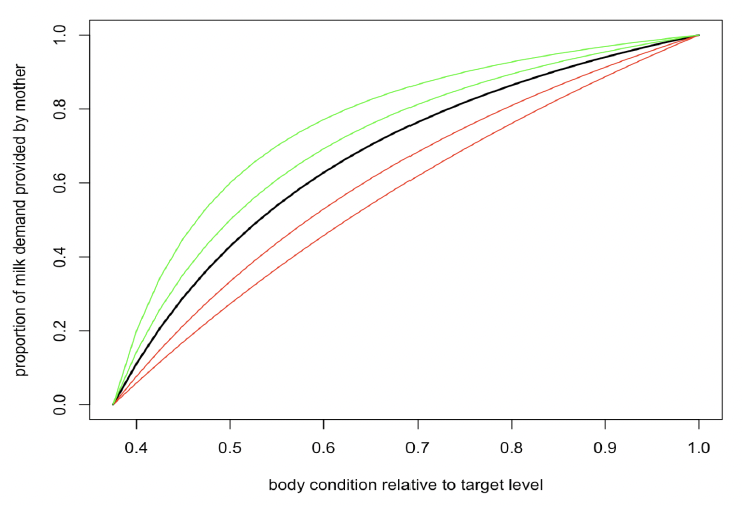
Lactation scalar (ΦL) is analogous to R; because ΦL determines the maximum amount of energy a calf/pup can obtain from milk on day t, where Sc,t is the structural mass of the calf/pup on day t. Hin et al. (2019) estimated ΦL for pilot whales on the assumption that the female provides all of her calf’s energy needs up to age TC. They calculated the mean amount of energy expended each day by the calf during this period for maintenance and growth, and then divided this by the average structural mass of the calf x 0.5 (on the assumption that the body condition of both mother and calf was equal to ρ). Similar calculations can be performed for other species, provided a value for σG (the energetic cost per unit structural mass) is available.
4.4.19 Mortality
Age-dependent mortality rate Hin et al. (2019) calculated an age-varying mortality rate for pilot whales based on published estimates of age-specific survival rates. A similar procedure can be used to estimate this rate for the five species modelled here from the age-specific survival rates provided in published estimates (Winship 2009, Arso Civil et al. 2019, Sinclair et al. 2020)
The starvation body condition threshold (ρs) represents the point at which further reduction in body condition is likely to have a negative effect on survival. It can be estimated from the ratio of blubber: total body mass of dead or dying animals that exhibit symptoms of terminal starvation (Kastelein and Van Battum 1990, Koopman et al. 2002).
Starvation-induced mortality rate (μs) This parameter determines how long an individual is likely to survive if its body condition falls below the starvation body condition threshold (ρs). Probability of survival is modelled as:
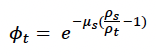
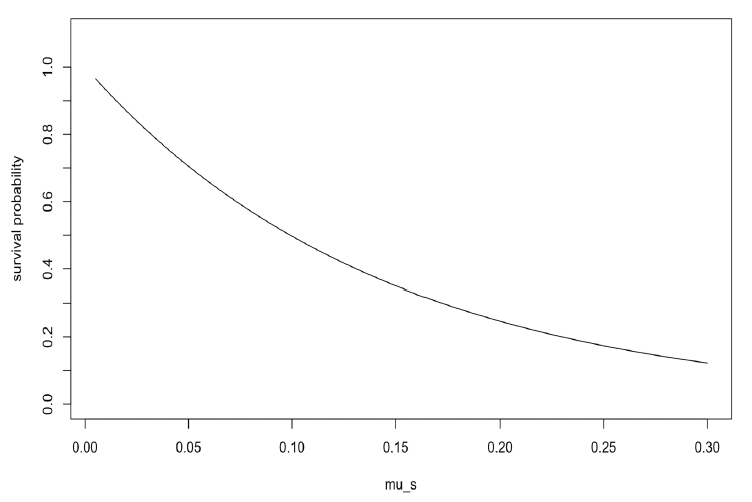
Higher values of μs result in a lower probability of survival (Figure 7). Hin et al. (2019) used a value of 0.2, which implies that 50% of starving individuals will survive for one week if their body condition remains below the threshold.
4.4.20 Modelling disturbance
Users can define the start and end points (Diststart and Distend) of the period during which disturbance can occur, and the number of days on which disturbance occurs (Distdur). Specific days when disturbance occurs are chosen at random within the defined period. During each day of disturbance, the resource density experienced by a simulated individual, and consequently the amount of energy it assimilates, is reduced by Disteffect. The effects of this reduction on energy assimilation will depend on the age and life history stage of the affected individuals, and the user can define the age classes that are affected using the parameter Agedist. In the current version the disturbances occur in a single year and their effect on vital rates are determined within the same time frame (for example, the survival of calves/pups that are alive at the time of the disturbance or are born shortly after it).
Contact
Email: ScotMER@gov.scot
There is a problem
Thanks for your feedback