Scottish Marine and Freshwater Science Vol 6 No 6: Development of a Model for Predicting Large Scale Spatio-Temporal Variability in Juvenile Fish Abundance from Electrofishing Data
Models of juvenile salmonid abundance are required to inform electrofishing based assessment approaches and potentially as an intermediate step in scaling conservation limits from data rich to data poor catchments. This report describes an approach for mo
Model Development
Because a combined model of capture probability and fish density was not considered to be practical for a national scale model due to computational complexity, a two stage approach was developed here. Capture probability was modelled assuming independent estimates of densities for each site visit ( i.e., a full density model). Spatio-temporal variability in density was then modelled based on these estimates of capture probability. The two main advantages of this modelling process are 1) model selection is simplified because only one aspect of the model (capture probability or spatio-temporal variability in density) is being tested at a time and 2) conditional modelling of density based on previously estimated capture probabilities allows the use of generalised additive models ( GAMs) and structural additive regression ( STAR) models (Fahrmeir et al., 2013). This allows the incorporation of a wide range of penalised smoothers and spatial and random effects as well as the option of using a negative binomial distribution over the Poisson to allow for additional Site Visit variation.
Development of a Two Stage Model: Model Theory
The joint likelihood for capture probability (p) and fish density (λ) can be defined as:
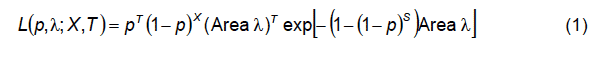
where, T = n 1 + n 2+…+n S, and X = n 2 + 2n 3+…+(S-1)n S and n i ( i = 1, …, S) is the number of fish caught on the ith of a total of S passes and Area is the area fished.
Stage 1: Capture probability model
For any given capture probability the estimated fish density for a site visit can be defined as:

Because the estimate of λ can be written in terms of p (Eqn. 2), it is possible to define a likelihood for p in terms of Z = X/T and T as follows:
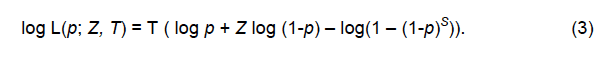
Capture probability can then be modelled in relation to covariates using the logistic link. The likelihood defined in (Eqn. 3) can then be used in model selection.
Stage 2: Fish density model
Given an estimate for capture probability, p, the distribution of T is Poisson with expectation:

Given estimates of capture probabilities from Stage 1, densities can be modelled on the log link using GAMs and incorporating an offset of log Area + log (1‑(1‑ p) s). Because electrofishing data are often more variable than assumed by a Poisson distribution a negative binomial distribution can be used to account for over dispersion.
Covariates and Model Selection
Both capture probability and densities can be modelled in relation to categorical, linear or smoothed covariates. While the incorporation of standard smoothers or those describing regional spatial variability are possible in mgcv, River Connectivity cannot be fitted in the standard package. This may be important in situations where sampling points are geographically similar, but are far apart in terms of river network distance. Similarly, there are no existing packages that can allow covariates to be added to capture probability models (above). These requirements were considered during this project where a new package was developed to combine and extend existing functions in R, particularly from the packages mgcv and igraph and to a lesser extent the spatial package maptools, rgdal, rgeos.
In the case of capture probability, the model building functionality of mgcv (Wood, 2011) was used to generate a design matrix to include covariates in the likelihood from (Eqn. 3) to allow rapid specification of complicated models. However, this method does not currently allow the use of generalised cross-validation to determine the degree of smoothing and as such is necessary to specify fixed degrees of freedom.
One of the main benefits of the two stage modelling approach was the ability to rapidly specify, fit and compare between models In the case of the capture probability model this can be achieved using BIC (Schwarz, 1978). However, in the case of the density model (which is a GAM), it is possible to use more sophisticated (ridge regression) model selection from the MGCV package to automatically remove terms.
Software: Data Preparation Requirements and Model Specification
The models and model fitting were provisionally implemented in an R package 'CLModel'. The package is currently only available within MSS pending testing and peer review of the methods. The package has the following dependencies which are available from CRAN: mgcv, igraph, maptools, rgdal, rgeos, sp, spdep. In addition, the library rstan is required and this is obtained from its own dedicated website ( http://mc-stan.org/rstan.html).
Data Preparation
Data should be prepared in a data-frame with covariates stored in columns and lines representing site visits. The package is flexible in terms of column headers, but the data-frame must contain the number of fish caught on each pass (separate columns) and the number of passes. Where there is an incomplete set of covariates these data are excluded from any model fitting, although this was not a concern in the current exercise. The function 'getData' must be run on the data-frame to provide electrofishing summary statistics before any further analysis. Following estimation of capture probabilities, it is necessary to calculate an offset before modelling fish densities. This is done using the function 'getOffset' or manually (see 'Development of a Two Stage Model' above). If calculated manually this should be stored in a column labelled 'offset'.
In the following examples the data is assumed to reside in a data-frame called 'Electrofishing'.
Adding Factors, Linear Effects and Smoothers
Factors ( e.g., Organisation or HA), linear effects ( e.g., Width) and smoothers ( e.g., DoY) can be specified for the capture probability model as follows:
| efp(Z ~ Organisaton + Width + s(DoY, k=3), data = Electrofishing) |
where in this example DoY is restricted to a smoother with 3 degrees of freedom. Similarly in the case of the fish density model:
| gam(T ~ HA + Width + s(DoY, k=6), offset = offset, data = Electrofishing) |
where this time, because the flexibility of the smoother is estimated from the data, a larger (maximum) degrees of freedom can be safely specified. Other standard GAM functionality remains. A range of 'smooth types' are possible e.g., thin plate splines with shrinkage (bs='ts') or random effects (bs='re') as in
| gam(T ~ HA + s(Catchment, bs='re') + Width + s(DoY), offset = offset, data = Electrofishing) |
where HA is modelled as a factor and catchment as a random effect.
Adding Regional Smoothers
Regional covariates such as HA could be estimated independently ( i.e. as a factor), but given spatial correlation it is more appropriate to fit a model where neighbouring regions have similar effects. This requires specification of the spatial (neighbourhood) structure using poly2nb and nb2mat functions in the spdep package. The shape file should be read into R using readOGR from the rgdal package and stored in an object (in this case 'ha') where the neighbourhood connections are calculated and converted to an adjacency matrix before conversion to GMRF using the function 'getRegional GMRF' from the CLModel package.
| ha_adj <- poly2nb(ha, queen = FALSE) Qha <- getRegionalGMRF(ha_adj) |
The regional effect for HA is then specified using bs='gmrf', a smoother type extending mgcv functionality developed for the CLModel package.
| gam(T ~ s( HA, bs='gmrf', xt=list(penalty=Qha)) + |
Although it is possible to incorporate spatial smoothers using existing functionality in mgcv, the 'gmrf' extension provides a more flexible interface that can be used to fit both regional and network scale effects. It can also automatically accommodate regions without observations but where there is information on spatial structure. By default the maximum degrees of freedom for regional smoothers would be equal to the number of regions. However, this can be restricted using by specifying a lower value e.g., 'k=10'. If a regional smoother were to be included in the capture probability model, restricted degrees of freedom should be specified.
Adding A River Network Smoother (River Connectivity)
Although a River Connectivity model can be applied to single catchments, it has not yet been possible to extend this functionality across multiple catchments. Consequently, in the following, the data-frame 'Electrofishing' is assumed to contain information from a single catchment. River Connectivity (see Covariates section above) is stored as a graph object and calculated using the 'buildTopo' and 'reduceNetwork' functions in the CLModel package incorporating functionality from the rgeos and igraph packages. The function 'getWRW1Mat' in the CLModel package converts the graph object into a GMRF.
| graph <- buildTopo(rivs) graph <- reduceNetwork(graph) Qrc <- getWRW1Mat(graph) |
The 'getRCLocation' in the CLModel package is then used to identify the location of sites on the network and to link to the GMRF ( i.e., generate River Connectivity covariate).
| Electrofishing $ RC <- getRCLocation(Electrofishing, graph) |
A model containing River Connectivity can then be specified as follows:
| gam(T ~ s(RC, bs='gmrf', xt=list(penalty = Qrc)) + Width + s(DoY), offset = offset, data = Electrofishing) |
Predicting
It is straightforward to predict fish densities on a river network smoother using standard methods in mgcv. In the following simple example, the densities are predicted only on the basis of RC and the model fit is stored as an object 'm'. Predictions are then made across the entire network by:
| m <- gam(T ~ s(RC, bs='gmrf', k=12, xt=list(penalty = Qrc)), offset = offset, data = Electrofishing) pred <- predict(m, newdata = data.frame(RC = V(graph)$name)) |
In the case above the new data-frame used for prediction consists of a single column 'RC', containing the id's of all the nodes on the entire river (sites and confluences).
Contact
There is a problem
Thanks for your feedback