Effects of displacement from marine renewable developments on seabirds breeding at the Isle of May

2. Methods

2.1. Study Area and Species

The Isle of May NNR, south-east Scotland (56°11'N, 02°33'W) is part of the Forth Islands SPA ( http://www.jncc.gov.uk/pdf/SPA/UK9004171.pdf). This SPA is designated for its numbers of common guillemot (hereafter 'guillemot'), razorbill Alca torda, Atlantic puffin

Fratercula arctica, lesser black-backed gull Larus fuscus, northern gannet Morus bassanus, European shag Phalacrocorax aristotelis, great cormorant P. carbo, roseate tern Sterna dougallii, common tern S. hirundo and sandwich tern S. sandvicensis.

This pilot study focused on one species for which a large body of empirical data exist from the Isle of May, the guillemot. The guillemot is the third most numerous breeding species in the Forth Islands SPA, after northern gannet and Atlantic puffin. The population has been in sharp decline in the last decade from a peak in 2001 of c. 30,000 pairs to the current population of ca. 18,000 pairs (Pickett & Squire 2011; Bruce 2011). The guillemot is a pursuit-diving seabird that preys primarily on small, shoaling fish such as lesser sandeels Ammodytes marinus and sprat Sprattus sprattus (Harris & Wanless 1985; Wilson et al. 2004). It breeds in dense colonies on cliff ledges, and both parents share the duty of incubation and rearing the single offspring. Typically, one parent attends the young whilst the other is at sea.

There is a paucity of published data on the behaviour of breeding guillemots in response to wind farms. The best current evidence on displacement is for non-breeding individuals available from wind farm developments outside the UK. Studies at Horns Rev wind farm, Denmark, suggest that guillemots did not forage in or travel through wind farms (Petersen 2005). However, patterns were less clear cut at the Egmond wind farm, off of the Dutch coast, with displacement recorded in some situations but not others (Leopold et al 2011), and there was no evidence of displacement of guillemots from Belgian developments (Vanermen et al. 2011). The development of offshore wind farm sensitivity scores for seabirds (Garthe & Hüppop 2004) ranked guillemot 20 ^th out of 26, although this low relative vulnerability score was primarily due to the low collision risk for this species. Guillemots were scored as moderate to high vulnerability for two of the factors most pertinent to displacement ('habitat use flexibility' and 'adult survival rate'). In accordance with this, the guillemot was ranked 11 ^th out of 38 in the list of species of concern due to disturbance and/or displacement from habitat due to offshore wind farms by Furness & Wade (2012). The inconsistent results obtained from empirical studies, paucity of published information on displacement of breeding individuals, and moderate to high vulnerability to displacement compared to other seabird species in the two reviews on seabirds, highlight the importance of a displacement model for this species for the outer Forth and Tay region.

2.2. Simulation Model

A model was created to simulate the feeding location of 1000 guillemots (ca. 6% of the SPA population) over a 24 hour period during chick-rearing (see Appendix 1 for details of model input parameters including sources). The simulation model allowed guillemots to choose the most suitable location for feeding during one foraging trip from the colony. The model incorporated realistic assumptions based on the known behaviour of guillemots (Section 2.2.2.) to deduce what the best location would be. The location of the 1000 guillemots and information on their chosen location are stored for each simulation. The model incorporated the Isle of May and the surrounding sea and land (OS Grid reference of bounding box of the model: xmin 332451 ymin 676319, xmax 423657, ymax 747098, area: 6532km ²). The resolution of the model was defined by the resolution of the input datasets (1 km ²). The model was run using the statistical software R v 2.14.1(R Development Core Team 2012).

2.2.1. Input layers

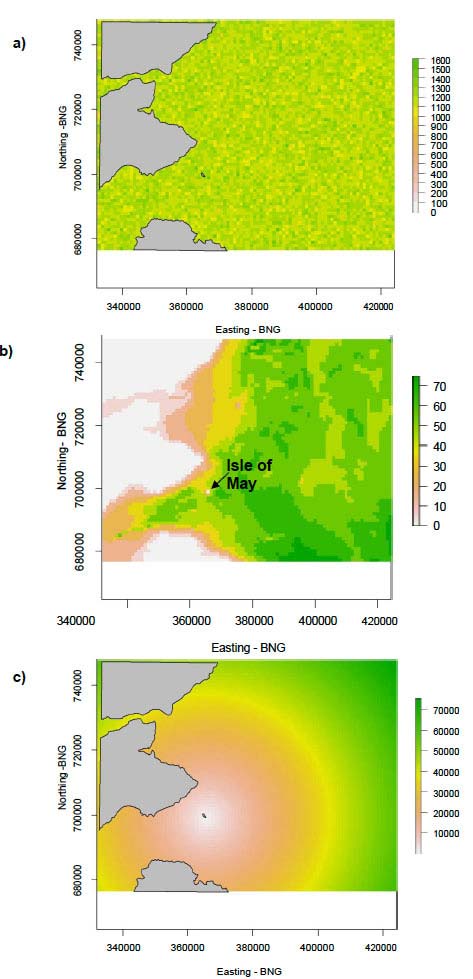
For the model to run successfully, three input layers were required (Figure 1): a prey density distribution across the area, the bathymetry of the area (maximum possible dive depth for the bird) and the distance of each location from the Isle of May (OS Grid Reference 365679, 699182). The bathymetry of the area was obtained from the British Geological Survey under licence ( http://www.bgs.ac.uk/products/offshore.html) and the distance of each location was calculated using the raster package in R (Hijmans & van Etten 2012). The prey density distribution was simulated using the rMatClust function in the R package spatstat (Baddeley & Turner 2005). This function generates a random number of points representing prey individuals, such as lesser sandeels or sprat, inside the bounding box of the model. The function also generates a Matérn's cluster process which entails, for each point, adding more points to create groupings of points. As the level of clustering increases, more points occur within groups and distances increase between groups. Unfortunately, no empirical data on fish shoal size and distribution were available for use in the model, so it is uncertain how realistic is the clustering level selected for examination here. However, it is likely that a clustered distribution is more realistic than the random distribution. A grid is placed onto the surface of points and the points summarised to create a prey density value for each 1km ² location. We used linear distances, but note that this would underestimate distances for some areas, notably in the Firth of Tay, which birds can not travel to directly.

The input layers were used to create a set of rules to enable the simulated guillemots to choose the best location to forage. The most suitable location was defined as being less than 50km and greater than 0km from the Isle of May based on empirically determined distributions of chick-rearing adults from animal-borne instrumentation spanning several years (Wanless et al. 1990; 2000; 2005a; Thaxter et al. 2009; 2010; Daunt et al. 2011a; b), the depth at the location had to be greater than 0m (guillemots are entirely marine, Cramp 1985) and there had to be one or more prey individuals at the location (for example, one or more lesser sandeels). If more than one location met these criteria then the cells were ranked so that the location that had the lowest dive depth, the smallest distance and highest prey density was the one chosen (based on optimal foraging theory that individuals would maximise gain and minimise cost, Stephens & Krebs 1986). The prey density layer was updated after each guillemot had chosen a location to account for prey being consumed and/or dispersed after feeding (Ashmole 1963; Lewis et al. 2001). The update was applied through the interference competition model of Hassell & Varley 1969:

a ⁱ = Q*P ^-m

Where a ⁱ is the intake rate of an individual, Q is the intake rate achieved by a single forager, P is the density of individuals at the site and m is interference coefficient. The interference coefficient determined the strength of the density dependent reduction in intake rate. For example, by increasing the interference coefficient, the maximum intake rate achieved by an individual will be decreased. For the simulation, Q was set at 0.4, P was taken from the number of guillemots at a location in the simulation and m was set at 0.6. The values of Q and m were obtained from both expert opinion and other interference competition studies on birds (Ens and Goss-Custard 1984, Dolman et al. 1995, Goss-Custard et al. 1995).

Figure 1. The three simulation model input layers required each at 1km ² resolution and land is shown in grey. a) Prey density distribution - scale bar is number of prey individuals. b) Bathymetry data - scale bar is in depth (m), c) distance map layer - scale bar is the distance (m). Northings and Eastings are in the British National Grid ( BNG) reference system.

2.2.2. Guillemot behaviour

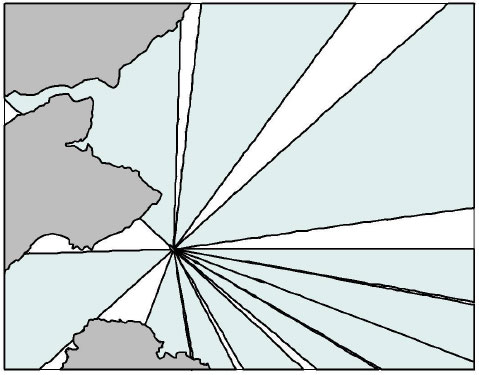
When guillemots fly away from the colony they typically do so on a bearing which they continue to fly on until they reach their first foraging destination (Daunt et al. 2011a,b). This behaviour was incorporated into the model using the distribution of empirical data on directions of guillemot flight for 159 trips from 54 individuals recorded in 1999, 2002, 2003, 2005 and 2010 (Thaxter et al. 2009; 2010; Daunt et al. 2011a; b). We considered it preferable to use empirical data on flight directions than assume that flight direction was random. For each guillemot in the simulation, a direction was sampled with replacement from the data. The summary statistics of the flight direction distribution were then used to estimate a number of sectors to restrict the flight path of guillemots in the simulation and, therefore, the feeding locations potentially available to them on that foraging trip. A total of 11 sectors were created in ArcMap v10 using the Sectors Tool (downloaded from the ESRI Mapping Centre). This required the bearing, sector angle, radius and centre coordinates in latitude and longitude for each sector. The sectors were different sizes to distribute the number of different bearings evenly (Figure 2).

Figure 2. The 11 sectors (blue polygons) used in the simulation model to represent the distribution of guillemot flight directions from the Isle of May. The grey polygons represent the land.

Guillemots depart the colony either singly or in flocks. Therefore, the simulation code was adjusted to account for variation in the number of birds departing the colony simultaneously. The estimates of flock size were based on data from 535 birds from colonies at Fowlsheugh and St. Abbs (Daunt et al. 2011c). The flock size ranged from 1 to 50 birds and a negative binomial distribution was fitted to the data. In the simulation, a flock size was sampled from this distribution and coupled to the direction of flight. For example, if a guillemot left the colony on a bearing of 45 ^o with a flock size of 5, then the next 4 guillemots in the simulation would also need to find a suitable location within the sector that incorporates 45 ^o. After the five simulated guillemots had chosen a location, the 6th bird would fly in a different direction.

It was assumed that when shoals were disturbed by the foraging activity of guillemots, prey availability will be adversely affected, for example because shoal size is reduced and/or the shoaling behaviour of the fish breaks down (Lewis et al. 2001). To incorporate this in the simulation model, an exponential decay function on the effect of prey availability was added:

prey = exp(-λd _ij )

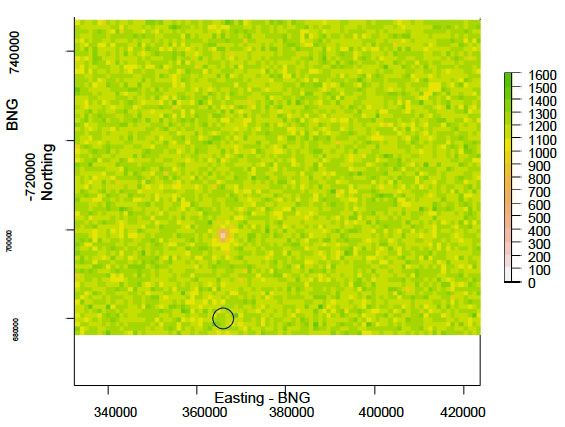
Where λ controls the level of the decay (decay constant) and d _ij is the distance between points i and j. After exploring a range of decay rates using simulated data to find the most appropriate effect distance (expert opinion), a decay rate of 0.001 was used with the distance layer calculated previously to obtain a decay rate distribution surface for the simulation. The decay rate distribution and the prey density layer are multiplied together to obtain a halo (sensu Lewis et al. 2001) of reduced prey availability around the Isle of May (Figure 3). For the set of input parameters used here the halo effect was detectable up to a maximum distance of approximately 8km from the Isle of May.

Figure 3. The prey density map used in the simulation model with a halo of reduced prey density shown in the circled area. Scale bar is the number of individual prey within a cell. Easting and Northing are in the British National Grid ( BNG) reference system.

2.2.3. Wind farm presence

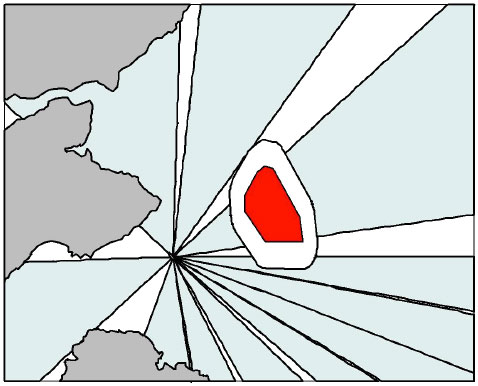
The simulation was modified to incorporate the presence of Neart na Gaoithe wind farm within the model area (Figure 4). When a suitable foraging location was chosen by a guillemot, then if that location was in the area of the wind farm as defined by the red polygon (Figure 4), then the bird had to move to a new suitable location within a 5km buffer zone of the wind farm (Figure 4). The assumption of the model was that guillemots had no prior knowledge of the wind farm location and therefore may fly out in the direction of the wind farm and will then need to feed in a suitable location close by.

Figure 4. The location of the Neart na Gaoithe wind farm (red polygon) and the 5km buffer zone (white polygon) used in the simulation model. The grey polygons represent land and the blue polygons mark out the sectors of bird flight direction.

2.2.4. Model Output

The simulation model produced a foraging location map of 1000 birds, the depth at that location, the prey density at the location and the distance of the location from the Isle of May. This information was used to calculate the flight and foraging cost incurred by the guillemots (see Section 2.3). The simulation was repeated 50 times to obtain a mean and standard deviation of guillemot locations. When the wind farm was present within the model the number of birds that were displaced to a new location was counted. In addition, the number of birds for which the wind farm acted as a barrier to movement, either on their outward journey, return journey or both by the wind farm, were recorded. It was assumed that birds would have to fly around the wind farm, hence increasing the distance travelled and associated flight costs.

2.3. Cost Model

The output of the simulation model was used to calculate the time cost incurred by the guillemots at their chosen feeding location. The cost model was an expanded version of that used in Daunt & Wanless (2008) and Wanless et al. (1997). The cost was separated into flight cost and foraging cost for each guillemot. The simulation model generated information about one foraging trip per guillemot and the cost incurred on this trip was multiplied by the average number of trips a guillemot makes per day during chick-rearing (2.02 trips) to obtain a valid cost for a period of 24 hours. This estimate is based on empirical data from 2002-03 (Enstipp et al. 2006), supported by a very similar value recorded in 1981-84 (Harris & Wanless 1985).

2.3.1. Flight Cost

The flight cost incurred by the guillemots was the time taken to travel the distance both to and from the chosen location. This was calculated as the distance travelled multiplied by 2 (assuming the same return path from the location) and divided by the mean flight speed for a guillemot (19.1 ms ^-1; Pennycuick 1997).

2.3.2. Foraging Cost

The foraging cost calculated from the simulation was defined as the amount of time the guillemots spend foraging to meet both the daily energy requirements of the adult and 50% of the daily energy requirement of the offspring (assuming that two parents share the costs of provisioning equally). Daily energy expenditure is multiplied by the assimilation efficiency (0.78, Hilton et al. 2000b) to obtain the total daily energy requirement of the guillemot.

The adult daily energy requirement is the total energy needed by the guillemot to fly to the suitable location in the simulation plus the energy required carrying out other activities such as resting on the sea surface and the length of time spent at the colony. The time spent carrying out these activities was multiplied by activity-specific energy costs taken from the literature (Flight energy cost: 7361.72 kJ day ^-1, Pennycuick 1987, 1989; resting at sea energy cost: 810.28 kJ day ^-1, Croll & McLaren 1993; time at colony energy costs: 1168.91 kJ day ^-1 Hilton et al. 2000a) . The energy costs are then added to the cost of warming food (51.92 kJ, Grémillet et al. 2003). The mean daily energy requirement of a guillemot chick was based on provisioning rates recorded at this colony (221.71 kJ day ^-1, Harris & Wanless 1985). The daily energy requirement was converted into grams per day assuming a mean energy density of 6.1 kJg ^-1 (Harris et al. 2008). Only total flight time could be calculated from the output of the simulation model to estimate the daily energy requirement. Therefore, the time spent resting at sea and at the colony was estimated from the distribution of empirical data on activity budgets of 18 birds (Wanless et al. 2005a). There are a number of sources of potential error when calculating daily energy budgets. Activity specific costs are typically estimated in captive studies, and it is possible that wild individuals are not equivalent. Assimilation efficiency has also been estimated in captivity. The mean flight speeds used in the calculation of flight costs may not be entirely accurate, and are likely to vary among individuals dependent on environmental conditions (in particular wind speed and direction). The mean energy density of prey is also expected to vary, as demonstrated from analyses of interannual variation (Wanless et al. 2005b).

The amount of time guillemots spent foraging to meet their daily energy requirements was assumed to depend on the prey availability at the chosen location. This relationship was defined in the cost model by incorporating a functional response between prey intake rate and prey density (Figure 5; Enstipp et al. 2007). This relationship assumed a maximum prey intake rate of 5 g min ^-1 and that the intake rate does not start to increase significantly until there is a prey density of 200 individuals per km ². A prey capture rate is obtained by multiplying the prey intake rate by the diving efficiency. The diving efficiency was included to account for the extra cost incurred with increased dive depth and it is obtained using the following equation: (Daunt & Wanless 2008):

Dive efficiency = 0.36 - (0.0021 * dive depth (m))

The depth at the feeding location was obtained from the simulation and used in the equation to calculate the diving efficiency. Using water depth at the location would assume all dives were benthic. However, guillemots are known to forage throughout the water column with a bimodal distribution of foraging depth (Daunt et al. 2006). To allow for this, depth at the location for 50% of the birds was sampled from a normal distribution with a mean of 11.71 m and a standard deviation of 8.07m (the distribution was obtained using empirical data, Daunt & Wanless 2008). The prey capture rate was then used to calculate the foraging time required by the bird to meet half of the daily energy requirement (foraging for one trip). If the total foraging time was greater than 12 hours for one trip then the birds would not be able to fulfil their daily energy requirements.

2.3.3. Wind farm specific costs

The flight and foraging costs calculated for the simulation results with a wind farm were the same as above, but with additional costs due to increased distance travelled. The additional distance travelled between the first chosen suitable location and the new location the guillemot was displaced to was included, as well as the distance from the Isle of May to the first location on the outward journey and the distance from the final location back to the Isle of May on the return journey. The presence of the wind farm may not only displace birds to a new location, but may also be a barrier to movement such that birds fly around it, therefore incurring increased flight time. Guillemots with a final location beyond the wind farm, but which were not displaced directly by the wind farm, had an additional outward distance to travel. The additional outward cost was sampled from a normal distribution with a mean of 20km and standard deviation of 5km due to the size of the wind farm (birds would need to fly around the wind farm which would be approximately half of the 40km perimeter). Guillemots with a final location also beyond the wind farm, whether they were displaced or not by the wind farm, would also incur an additional return cost to fly around the wind farm. The return cost was also sampled from the same distribution as the outward cost.

2.4. Scenarios

The simulation and cost models were run both with and without the presence of the wind farm using the following scenarios:

1. The prey density layer was assumed to have a random distribution across the model area (Figure 1a).

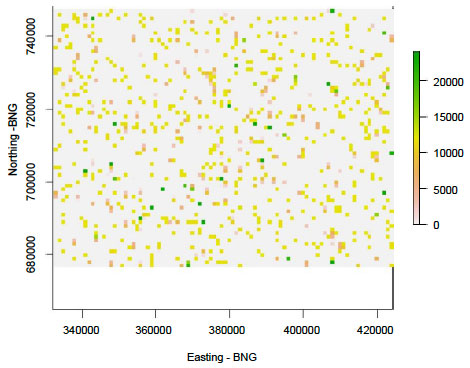
2. The prey density layer was changed to give a more clustered distribution across the model area (Figure 5). The number of prey individuals across the surface was the same as the random distribution, but the degree of clustering was increased to give a more realistic representation of fish shoals within the individual locations.

3. The interference coefficient in the simulation model was increased to 0.9 to simulate more intense interference competition between foraging guillemots that might occur if prey availability decreased.

Figure 5. The clustered prey distribution used in Scenario 2 to represent prey items as a shoal. Scale bar is the number of individuals in each cell. Northings and Eastings are in the British National Grid ( BNG) reference system.