Scottish Schools Adolescent Lifestyle and Substance Use Survey (SALSUS): Technical Report 2015

Precision of results and measurement of change

Survey respondents represent only a sample of the total population of 13 and 15 year old pupils in Scotland, and results are therefore subject to sampling error. The sampling error is the amount by which the value of a sample estimate for a particular parameter is expected to differ from its true value in the population sampled from. This means that observed differences between sub-groups may have occurred by chance. Throughout the report only differences that are statistically significant, where we can be 95% confident that such a difference has not occurred by chance (p<0.05), are commented upon.

The formula for calculating the sampling error ( SE) of a simple random sample is:

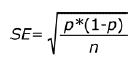where p = the estimate of the parameter and n=sample size.

The formula for calculating the sampling error for the differences between two estimators (p1 and p2) derived from two independent samples (assuming a simple random sample) is:

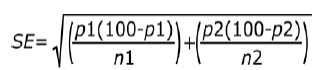
Rather than using a simple random sample, whole classes were sampled within the schools that agree to participate. Therefore, classes were clustered within those schools, and pupils are clustered within those classes. Pupils within the same class and within the same school were more likely to be similar to each other, and therefore values cannot be assumed to be independent of one another. Further details on the calculation of standard errors and design effects are provided below.

It is important to recognise that sampling error is only one of the sources of error that affect the accuracy of survey results. Other sources of error include response bias (previously discussed) and over/under reporting, both of which are difficult to quantify.

Calculating standard errors and design effects

The sample design of SALSUS is complex, involving stratification by local authority and school type (state or independent), as well as clustering within schools. In addition, weights were applied when obtaining survey estimates.

Complex design and weighting affects standard errors for survey estimates, which are generally higher than the standard errors that would be derived from an unweighted simple random sample ( SRS) of the same size. For example, clustering reduces the precision of estimates, whereas stratification can increase precision. Weighting can also reduce the precision of estimates.

The ratio of the standard error of the complex sample to that of a simple random sample of the same size is known as the design factor. Put another way, the design factor (or 'Deft') is the factor by which the standard error of an estimate from a simple random sample has to be multiplied to give the true standard error of the complex design.

A Design Factor greater than 1.0 indicates a confidence interval wider than it would be with simple random sampling, meaning that the precision of estimates is reduced. A Design Factor of less than 1.0 indicates a narrower confidence interval and greater precision.

The true standard errors and Defts for SALSUS 2015 have been calculated in STATA using Linearization (Taylor series method), also known as the propagation of variance by Kish, and was the method used from 2006 to 2013. Thirty-six strata were included for the calculation of standard errors and Defts, one for each combination of local authority and school type (state or independent sector). For five local authorities: Dundee City, Fife, Inverclyde, Moray and Stirling, the variance between clusters could not be calculated for independent schools because there was only one independent school sampled in each of these local authorities. The independent schools in these ten local authorities were combined into one stratum to calculate sampling errors and Defts. There were 851 clusters used in the calculations, one for each class that participated in the survey ^[4] .

The Deft values applied and adjusted true standard errors (which are themselves estimates subject to random sampling error) are shown in Tables 5 to 10 for six key variables from the survey along with 95% confidence intervals.

When comparing the 2015 key variables with the 2013 key variables, significance tests were applied based on the 'pooled standard error' for each variable (a weighted sum of the true standard errors ^[5] for each year). Table 11 shows the six key variables for 2013 and 2015, with the true standard errors for each year and whether or not the difference is significant at the 5% level.

Table 5: Linearised standard errors and 95% confidence intervals for the proportion of pupils who are regular smokers, by age and gender: Scotland 2015

	Sample Size	Proportion	Linearised Standard error	Binomial Wald 95% CI		Defts
				Lower CI	Upper CI
13 year olds
Boys	6439	1.51%	0.19%	1.15%	1.88%	1.19
Girls	6712	1.65%	0.21%	1.24%	2.07%	1.29
15 year olds
Boys	5657	7.39%	0.48%	6.45%	8.33%	1.45
Girls	5595	7.21%	0.48%	6.27%	8.14%	1.44

Table 6: Linearised standard errors and 95% confidence intervals for the proportion of pupils who drink alcohol at least once a week, by age and gender: Scotland 2015

	Sample Size	Proportion	Linearised Standard error	Binomial Wald 95% CI		Defts
				Lower CI	Upper CI
13 year olds
Boys	6522	2.25%	0.24%	1.78%	2.71%	1.24
Girls	6743	2.38%	0.24%	1.91%	2.85%	1.22
15 year olds
Boys	5714	11.96%	0.59%	10.80%	13.12%	1.45
Girls	5607	12.98%	0.68%	11.65%	14.30%	1.58

Table 7: Linearised standard errors and 95% confidence intervals for the proportion of pupils who drank alcohol in the last week, by age and gender: Scotland 2015

	Sample Size	Proportion	Linearised Standard error	Binomial Wald 95% CI		Defts
				Lower CI	Upper CI
13 year olds
Boys	6166	3.83%	0.34%	3.16%	4.51%	1.35
Girls	6431	4.22%	0.33%	3.56%	4.87%	1.27
15 year olds
Boys	5485	15.89%	0.67%	14.57%	17.21%	1.44
Girls	5479	18.91%	0.78%	17.38%	20.44%	1.54

Table 8: Linearised standard errors and 95% confidence intervals for the proportion of pupils who have ever used drugs, by age and gender: Scotland 2015

	Sample Size	Proportion	Linearised Standard error	Binomial Wald 95% CI		Defts
				Lower CI	Upper CI
13 year olds
Boys	6193	5.80%	0.39%	5.03%	6.57%	1.28
Girls	6531	4.92%	0.37%	4.20%	5.65%	1.31
15 year olds
Boys	5476	20.89%	0.80%	19.33%	22.45%	1.53
Girls	5490	15.94%	0.69%	14.58%	17.30%	1.47

Table 9: Linearised standard errors and 95% confidence intervals for the proportion of pupils who have used drugs in the last year, by age and gender: Scotland 2015

	Sample Size	Proportion	Linearised Standard error	Binomial Wald 95% CI		Defts
				Lower CI	Upper CI
13 year olds
Boys	6193	4.92%	0.35%	4.23%	5.62%	1.24
Girls	6531	4.15%	0.34%	3.50%	4.81%	1.29
15 year olds
Boys	5476	18.78%	0.76%	17.28%	20.27%	1.52
Girls	5490	14.20%	0.64%	12.93%	15.46%	1.43

Table 10: Linearised standard errors and 95% confidence intervals for the proportion of pupils who have used drugs in the last month, by age and gender: Scotland 2015

	Sample Size	Proportion	Linearised Standard error	Binomial Wald 95% CI		Defts
				Lower CI	Upper CI
13 year olds
Boys	6193	3.14%	0.29%	2.58%	3.70%	1.24
Girls	6531	2.88%	0.27%	2.35%	3.41%	1.23
15 year olds
Boys	5476	13.44%	0.67%	12.13%	14.75%	1.52
Girls	5490	8.65%	0.51%	7.65%	9.65%	1.41

Table 11: Statistical significance of comparisons between 2013 and 2015 results for key variables

	2013 SALSUS			2015 SALSUS			T test (2 sided)	P - Value	Significant at the 5% level?
	%	True standard error	Sample size	%	True standard error	Sample size
Regular smokers
13 yr old boys	1.82	0.199	8518	1.52	0.188	6439	1.111	0.267	No
13 yr. old girls	1.71	0.166	8546	1.65	0.211	6712	0.208	0.835	No
15 yr. old boys	8.27	0.48	8080	7.39	0.478	5657	1.296	0.195	No
15 yr. old girls	9.00	0.467	7969	7.21	0.478	5595	2.648	0.008	Yes
Drink at least once a week
13 yr. old boys	1.90	0.212	8664	2.25	0.237	6522	-1.097	0.273	No
13 yr. old girls	1.82	0.177	8607	2.38	0.239	6743	-1.932	0.053	No
15 yr. old boys	11.86	0.513	8156	11.96	0.593	5714	-0.128	0.899	No
15 yr. old girls	11.25	0.512	8020	12.98	0.676	5607	-2.061	0.039	Yes
Drank in the last week
13 yr. old boys	4.08	0.255	8671	3.83	0.342	6166	0.571	0.568	No
13 yr. old girls	4.22	0.294	8617	4.22	0.334	6431	0.005	0.996	No
15 yr. old boys	18.37	0.634	8178	15.89	0.674	5485	2.661	0.008	Yes
15 yr. old girls	19.06	0.629	8027	18.91	0.780	5479	0.146	0.884	No
Taken drugs in last month
13 yr. old boys	2.34	0.198	8293	3.14	0.286	6193	-2.376	0.018	Yes
13 yr. old girls	1.75	0.166	8425	2.88	0.269	6531	-3.778	0.000	Yes
15 yr. old boys	10.92	0.494	7925	13.44	0.667	5476	-3.092	0.002	Yes
15 yr. old girls	7.83	0.405	7897	8.65	0.510	5490	-1.276	0.202	No
Taken drugs in last year
13 yr. old boys	3.81	0.289	8293	4.92	0.354	6193	-2.460	0.014	Yes
13 yr. old girls	2.82	0.222	8425	4.15	0.335	6531	-3.455	0.001	Yes
15 yr. old boys	16.68	0.682	7925	18.78	0.762	5476	-2.056	0.040	Yes
15 yr. old girls	14.30	0.559	7897	14.20	0.644	5490	0.122	0.903	No
Taken drugs ever
13 yr. old boys	4.79	0.322	8293	5.80	0.393	4	-1.998	0.046	Yes
13 yr. old girls	3.52	0.247	8425	4.92	0.369	6531	-3.281	0.001	Yes
15 yr. old boys	19.24	0.763	7925	20.89	0.797	5476	-1.496	0.135	No
15 yr. old girls	16.34	0.651	7897	15.94	0.695	5490	0.418	0.676	No