Scottish Marine and Freshwater Science Volume 6 Number 10: At-Sea Turnover of Breeding Seabirds - Final Report to Marine Scotland Science

3. Definition of Turnover

Turnover represents the value that a "snapshot" census of the population at any particular time would need to be multiplied by in order to obtain an estimate of the total population of birds using the area at any point during the breeding season. For example, if a snapshot census identifies 100 birds using the area, a turnover value of 10 would mean that 1000 birds are estimated to use the area during the entire breeding season. More precisely, we define the "turnover" associated with behaviour B (resting at sea, foraging, or flying) and spatial area A to be:

(Number of birds that perform behaviour B within area A at any point during the entire breeding season)/(Mean across time-points of the number of birds that perform behaviour B visiting area A at each time-point t)

Turnover, therefore, represents the ratio of the number of birds that use the area throughout the breeding season to the number of birds that would typically be seen if a comprehensive census survey was conducted at a particular time. Note that the definition is intrinsically linked to a particular spatial area A and a particular behaviour B. The area A typically corresponds to the footprint of an offshore wind farm.

In mathematical terms, the definition of turnover can be expressed as:

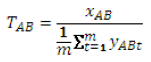
where x _AB represents the number of birds that perform behaviour B in area A at any point during the breeding season, and y _ABt represents the number of birds performing behaviour B in area A at time t and t = 1,..., m are an appropriately selected set of representative times.

Individual-based simulations are used to estimate both of these numbers. The survey at time, t, is assumed to be a complete snapshot census of the population within area A, and is assumed to occur instantaneously ( i.e. providing a complete "snapshot" of all the birds using area A during that time) - the possibility that birds will leave or enter area A, or will change behaviour during the course of the survey, is disregarded. This sort of "snapshot" survey is an idealised construct, because actual survey methods do not allow for a full census of birds to be collected instantaneously over such a large area. However, most survey techniques are designed to attempt to estimate such a snapshot of the population. Whilst they may not be able to achieve this for logistical reasons, they are designed to approximate the result that would have been obtained from an actual census snapshot survey. Therefore, in this project, we consider an idealised full census "snapshot" survey of the breeding individuals using area A at time t so that we may disentangle the effects of turnover from the effects of survey error and/or bias. The results that we obtain in this project regarding the effects of turnover will, therefore, be general, and not tied to a particular survey methodology.

In the following Sections, 3.2 to 3.4, we detail the species for which turnover is assessed, and describe the different scenarios considered within the project for capturing the level and spatial scale of fidelity, as well as the spatial location and extent of surveys. We then provided more detailed methodology for the implementation of these scenarios in Sections 3.5 to 3.6.

3.2. Choice of Species

The choice of the four species (black-legged kittiwake, common guillemot, razorbill and Atlantic puffin) for which turnover is assessed in this project follows on from the four main species considered in a previous project regarding the effects of displacement on foraging birds in the breeding season (Searle et al. 2014). The Northern gannet, Morus bassanus, was not considered here because the very large foraging range of this species would render estimating turnover a very computationally intensive task that would not have been possible to complete within the tight timescale of the current project. However, for gannet and five other species identified by Marine Scotland to be of interest (red-throated diver, Gavia stellata, black guillemot, Cepphus grille, European shag, Phalacrocorax aristotelis, common eider, Somateria mollissima and northern fulmar, Fulmaris glacialis) we have conducted a review of the published literature relevant to estimating turnover (for details see Section 2.1 and 2.2 above). For data rich species, we have provided input parameters for potential future turnover modelling work that could be conducted using the framework presented in this project; for data poor species, we have highlighted knowledge gaps and future data collection needs.

3.3. 'Level of Site Fidelity' and 'Spatial Scale of Site Fidelity'

(a) Level of Site Fidelity

The level of site fidelity within this project is set to vary between zero (representing the situation in which foraging locations are selected independently on each day) and one (representing complete site fidelity where the same foraging location is used throughout the breeding season). Because empirical data on the level of site fidelity is not readily available for these species, we estimate turnover at five arbitrary intervals along this continuum from zero to complete fidelity to capture a range of effects (0.0, 0.5, 0.67, 0.83, 1.0). These values for the level of site fidelity were chosen to best capture the change in estimated turnover at medium to high levels of turnover - where the greatest change in turnover per unit of site fidelity occurs (see Figures below; Section 4). The results will, therefore, demonstrate how the degree of turnover changes for each species as site fidelity increases. It follows that when fidelity is assumed to be complete (individuals forage and rest at the same location throughout the breeding season), turnover will approach a value close to one (when the spatial scale of site fidelity is at the resolution of a single grid cell; see below). In all simulations, central place foraging by breeding birds is assumed to take place.

(b) Spatial Scale of Site Fidelity

The spatial scale of site fidelity refers to the spatial extent of the area over which birds return to a previously used foraging location, thereby displaying site fidelity. As agreed by the Steering Group, we chose to consider turnover at three different scales of site fidelity:

• 1 x 1 grid cell or 0.5 km*1.0 km
• 20 x 10 grid cells or 10 km*10 km
• 100 x 50 grid cells or 50 km*50 km

3.4. Choice of Spatial Areas

We focus in this project upon four specific spatial areas A - the footprints that are associated with four recently consented wind farms in the Forth-Tay area of the east coast of Scotland - Neart na Goithe ( NNG), Inch Cape ( IC), Seagreen Alpha (Alpha), and Seagreen Bravo (Bravo); (Figure 3.1; full details are in Searle et al. 2014). These footprints each incorporate a 1 km buffer around the recently consented developments.

Figure 3.1: Map of study area showing SPAs and recently consented wind farms.

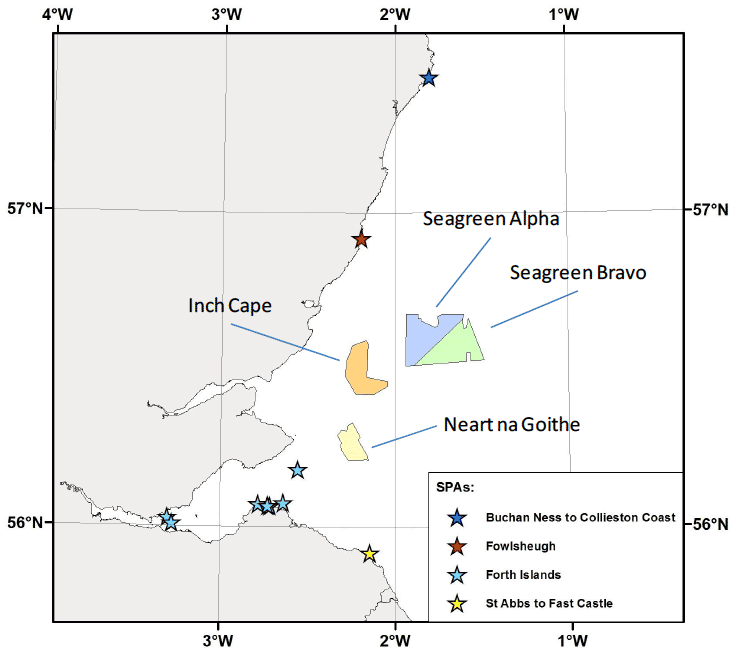
We also investigate the effect of the spatial scale of the survey area by considering "artificial" wind farm footprints centred on the median latitude and longitude of each recently consented wind farm (Figure 3.1). These "artificial" wind farms are assumed to be square, with a range of possible areas - 10 km ², 40 km ², 100 km ² and 200 km ². This covers the range of project scales that are commonly encountered and should provide an indication of the sensitivity of outputs to the area under consideration.

3.5. Choice of Behaviours

Studies of daily time budgets of birds during chick-rearing demonstrate that adults divide their time into four main activities - colony attendance, commuting flight to and from the foraging areas, foraging, and resting on the sea surface (Daunt et al. 2002). At-sea surveys classify birds into the latter three behavioural categories; therefore, in this project we consider turnover for birds in flight (commuting), foraging, or resting at sea. We also consider turnover for combined groupings of behaviours: (a) birds in flight or foraging, (b) birds that are foraging or resting, and (c) birds that undertake any of the three behaviours. This was done due to the difficulty that can exist during at sea surveys in distinguishing between foraging and resting behaviour of auks, or foraging and commuting behaviours of kittiwake.

3.6. Estimating Turnover

3.6.1. Defining Times

The level of turnover will depend on the time of day at which the survey is undertaken. In practice, surveys take place at a range of different times, so we simply assume that the survey time is randomly distributed between the earliest time that surveys typically occur (05:00 hours) and the latest time at which they typically occur (20:00 hours). We select R = 100 random survey times from within this interval for each of the D days in the breeding season. The choice of R = 100 is intended to balance accuracy (taking larger values of R reduces the stochastic noise associated with choosing individual survey times at random) and computational speed (the calculations become very slow if R is large).

3.6.2. Simulating Locations

We simulate the foraging locations and individual flight trajectories of birds from each of the SPAs within the vicinity of the recently consented wind farms using methods developed from GPS tracking data for each species (see Searle et al. 2014 for details). A percentage of the total population was simulated for each SPA (approximately 5,000 - 10,000 birds per species), following Searle et al. (2014). Briefly, for each species, bird densities were estimated from filtered GPS tracking data using a Binomial generalized additive model ( GAM). The GAMs provide an estimate of the predicted bird density for each species-by- SPA combination, which are then used to select daily foraging locations for each bird in the simulation. We assume that each bird will visit exactly one foraging location on each day (although it may do so more than once). Foraging locations are restricted in this way because it is very difficult to distinguish between different foraging locations from the tracking data. This assumption also avoids significant complexities associated with estimating turnover for individuals using multiple foraging locations per day, and is consistent with the previous approach used in Searle et al. (2014).

We assume that resting at sea occurs at the same location as foraging, and that each bird travels in a straight line between its colony and chosen foraging location. In reality there are likely times when the birds rest at locations different from the locations where they forage, however, it is not possible to separate foraging from resting behaviours with any certainty from GPS data alone. By making these assumptions we may then evaluate whether the bird travelled through the survey target area A to reach its selected foraging site.

In previous work (Searle et al. 2014), the foraging locations for each bird were originally simulated independently from day to day. However, this assumption disregards the possibility that birds are faithful to a particular site or spatial region (site fidelity) when foraging over a breeding season. While this is not critically important when assessing broad-scale effects ( e.g. the displacement effect from wind turbines), it is important when estimating turnover. We, therefore, modified the original simulation of foraging locations by assuming there is a spatial scale of site fidelity (represented by a regular spatial grid of one of three pre-determined spatial resolutions; 1 x 1 grid cell or 0.5 km*1.0 km; 20 x 10 grid cells or 10 km*10 km; and 100 x 50 grid cells or 50 km*50 km) that defines the extent of the area over which site fidelity operates. We also assumed there is a level of site fidelity, , which operates within this spatial area - a value of = 1 corresponds to complete site fidelity at the level of the regular spatial grid ( i.e. a bird will always return to the same cell on this spatial grid, although it will then choose locations within this spatial grid independently from day to day), whereas a value of = 0 corresponds to an independent choice of location on each day (sensu Searle et al., 2014). Note that = 0 does not correspond to a crude definition of "no site fidelity", because birds may return to the same spatial areas on multiple days. Rather it corresponds to "no more site fidelity than that which would arise by chance, based on independent choices on each day". Full details of the approach are given in Appendix A.

Our approach assumes that birds displaying foraging site fidelity go back to the same grid square, rather than assuming that they go back to a location that is within a particular distance of the original foraging location - so fidelity does not operate as a continuous function of distance away from the original foraging location. The regular spatial grid is used for convenience: the boundaries of grid cells are arbitrary, and are unlikely to correspond to the boundaries of actual foraging areas, but it is computationally tractable and provides a useful mechanism to explore how the spatial scale of fidelity affects turnover. We expect that turnover is likely to be more closely related to the level of fidelity and to the spatial scale of fidelity, than to the exact location or shape of the foraging areas used by birds.

To assess how estimates of turnover are influenced by the level of site fidelity () and the spatial scale of site fidelity we consider levels of site fidelity ranging from zero to one (0.0, 0.5, 0.67, 0.83, 1.0), and spatial scales of fidelity ranging from 0.5 km*1.0km to 50 km*50 km.

3.6.3. Time Activity Budgets

The simulations in Section 3.6.2 create the foraging, resting-at-sea and flight locations for each bird on each day, from which we determine whether each bird is exhibiting behaviour B within survey target area A. In order to translate these into the locations that are visited at a specific time, t, we need to account for daily time budgets of birds.

We do this through the use of "empirical activity budgets". A sample of breeding adults from each species have been deployed with a variety of data loggers from which daily time activity budgets were derived ( i.e. the proportion of time per 24 hours spent on each of the four principal activities of foraging, flying, resting on the sea surface and colony attendance; details are provided in the following papers: Daunt et al. 2002; 2006; Enstipp et al. 2006; Harris et al. 2012; Thaxter et al. 2013). We used these data to estimate the mean proportion of time that birds spent undertaking each of the four principal activities between 05:00 and 20:00 hours. By focusing on the period during which surveys take place we are able to account for diurnal patterns in activity.

The key potential issue with the empirical approach is that it assumes that all birds have, apart from random stochastic variation, the same time activity budget, and that this budget is the same for all foraging locations. This means, for example, that the time spent foraging may not be related to the estimated prey density at each simulated foraging location, as would be expected under optimal foraging theory. An alternative approach is to estimate the daily time budget using output from a mechanistic model, rather than empirical data. We investigated two possible ways of doing this, using the optimal foraging model of Searle et al. (2014) but after investigation (full details are given in Appendix B) we concluded that the empirical approach provides substantially more reliable estimates of overall time budgets than the model-based approach (which was not designed to accurately replicate the empirical activity budgets of birds), and we, therefore, only use the results of the empirical approach within this study.

3.6.4. Simulating Behaviour in a Snapshot

The times ( Section 3.6.1), locations ( Section 3.6.2) and behaviours ( Section 3.6.3) allow us to simulate, for a given bird at a particular time t on a particular day:

(a) its location; and

(b) the behaviour it is performing.

By calculating the locations and behaviour of all birds it is then straightforward to derive an estimate of turnover using the definition given in Section 3.1.