Scottish Marine and Freshwater Science Volume 5 Number 11: Assessing the status of Scottish Atlantic salmon (Salmo salar L.) stocks using reported catch data: a modelling approach to account for catch and release in the rod and line fishery

Appendix 1

The catch and release model has been developed to account for multiple recaptures of released fish in a rod fishery where both catch and release and the retention of landed fish is practiced. The probability of recapture following release is assumed to be equal to the exploitation rate (proportion available salmon captured) and independent of the number of previous releases.

In the simplest case, i.e. the absence of post handling mortality and where the fishery practices total catch and release, the relationship between the reported catch (R) and the number of salmon at first capture (C1) can be described by the following equations:

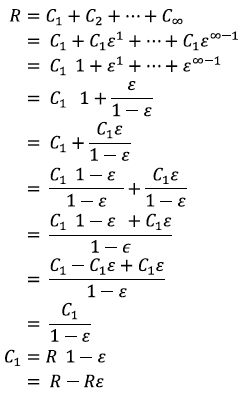
Where ε = the exploitation rate (proportion available salmon captured) and C­n = the number of salmon capture at catch number n.

The difference between the reported catch and the number of salmon at first capture can therefore be calculated as:

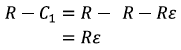
Expressed as a proportion of the reported catch (P) this becomes:

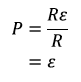
These equations can be expanded to include information on post handling mortality and retention of rod caught salmon by adjusting the number of fish available to be recaptured:

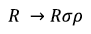
Where σ = proportion surviving once released and ρ = proportion of captured fish subsequently released.

The two main equations therefore become:

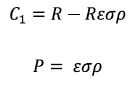
From this it can be seen that the influence of ε, σ and ρ is the same - i.e. a doubling of any of the parameters will lead to a doubling of the percentage error. As the proportion of captured fish subsequently released has risen by approximately ten times between 1994 and 2013 it is likely that this will have the biggest influence on any bias in the catch data.