Scottish housing market: tax revenue forecasting models – review

4. Extensions and complements

The following techniques and approaches could be applied to refine or augment the models described above to address methodological shortcomings or to offer researchers an alternative perspective.

Bayesian methods

Bayesian techniques have been applied across the different model classes evaluated in Section 3. Bayesian inference allows forecasters to use information not contained in the history of the variables of interest (the estimation sample). This is done by constructing prior distributions that describe the state of knowledge about parameters before observing the history of the outturn variables of interest- that is, the forecaster treats parameters that are known (or roughly known) as given (that is, they are not estimated within the model), and estimate the remaining unknown parameters. ^[39]

Bayesian inference can be useful under conditions of limited data to develop more complex, larger models, with more variables and more parameters. This may be relevant for the Scottish market, where data may be limited compared to the UK as a whole and other markets such as the United States.

Bayesian techniques are commonly applied to the VAR class of models discussed in Subsection 3.4. A Bayesian VAR ( BVAR) is a restricted VAR, in the sense that an informed value of one or more parameters is imposed on the model for estimation, rather than it being estimated over the historical sample. Specifically, instead of eliminating lags to cut down on the number of parameters that need to be estimated, the BVAR approach imposes restrictions on the coefficients of long lags by assuming that they are more likely to be zero than coefficients with shorter lags. ^[40] Another common restriction is that the coefficient of the first lag is assumed to have mean equal to one (Litterman, 1981).

The performance of BVARs for the housing market was assessed by Das, Gupta, and Kabundi (2010). They investigated whether information in a macroeconomic dataset of 126 time series can be used by large-scale BVAR models to forecast real house price growth in the US. They compared the forecast to small-scale VAR models, finding that forecasts over the first one- to 12- months ahead do not outperform smaller VARs.

Dynamic factor modelling

To overcome some important drawbacks of VAR modelling, such as the degrees of freedom problem (described above in Subsection 3.4), researchers have proposed incorporating vast data sets in a procedure called dynamic factor modelling (similar-and often synonymous-concepts include principal-components regression and factor-augmented forecasting). Dynamic factor modelling uses both observed and unobserved influences to forecast a system. To do so, the forecaster first examines the variables that can be observed and their relation to other observed variables. By subtracting this shared influence from the total behaviour of the system, all the unobserved factors influencing outcomes can be backed out. The behaviour of all the unobserved factors considered together can then be used to estimate a relatively compact equation.

Dynamic factor modelling can offer the best of both worlds-a model conditioned on a very rich, expansive data set, with the statistical advantages of working with only a small number of series. It relies crucially on the assumption that a large number of time series can be summarized by a small number of indexes.

Dynamic factor modelling has been applied to the housing market by researchers such as Gupta, Jurgilas, and Kabundi (2010). They used the factor-augmented VAR approach of Bernanke et al. (2005) and a large data set of 246 quarterly series over 1980 to 2006 to assess the impact of monetary policy on real housing price growth in South Africa. Gupta et al. found that real price growth responds negatively to interest rate increases, and that the effect is considerably larger for samples of large houses than small.

While some software packages are beginning to introduce libraries and add-ons for dynamic factor analysis, there would still be significant technical challenges to overcome, requiring analysts with a very specialised skill set.

Computable general equilibrium models

Computable general equilibrium models are similar in certain assumptions to DSGE models; however, CGE models are a snapshot in time, based purely on economic theory, and do not bring in the statistical dynamics of time series across time. Their evaluation algorithms provide a static long-run steady state solution for a set of prices that equates aggregate demand for all commodities and factor inputs with aggregate supply. They are not generally suited or used for forecasting.

That said, Dixon and Rimmer (2009) proposed a framework for CGE models that could be integrated into a macroeconomic forecasting framework to produce forecasts for the household sector. They run historical simulations for each year over history. By using that information and constraining the model to a separate forecast of macroeconomic variables, they arrive at forecasts for disaggregated individual commodities and sectors such as housing.

CGE models are useful for policy applications, most suitably tax efficiency and incidence analysis, international trade, and environmental analysis. HMRC uses a CGE model to assess these issues as well as the impact of tax changes on the macroeconomy. ^[41]

Maintaining a CGE model would require a dedicated team, and someone with a very specific skillset (almost certainly a PhD economist with research in that field). The cost of these external consultants can run between one and two full-time equivalent employees.

Predicting turning points

A useful trait of a new modelling approach would be the ability to predict market corrections. This is important not only for LBTT revenues, but also for the macroeconomic outlook and a wide range of policy reasons, given the power of the housing market to influence the rest of the economy.

While we came across few methods that were demonstrated to reliably predict when future bubbles will form and burst, probit models hold some promise to recognising whether the current period is a peak or trough. ^[42] Probit models estimate a result that lies between zero and one that reflects the probability of an event occurring, in this case the probability that a given quarter is a peak or trough in real house prices (with values lying closer to one meaning the event is more probable).

Rousová and Noord (2011) estimated a probit model across 20 OECD countries to predict possible peaks and troughs in real house prices in 2011 and 2012.

Estimation of the Rousová and Noord model involves three steps:

1. Identify local peaks and troughs over history using an indicator function that identifies local maximum and minimum over an arbitrary interval (the authors use 6 quarters, following Girouard et al. (2006) and Van den Noord (2006), but others, such as Crespo Cuaresma (2010) use as few as two).

2. Impose thresholds of minimum price changes before or after the turning points identified in Step 1 to screen out minor fluctuations, leaving only major peaks and troughs. The authors use an average increase of 15% during upturns (trough to peak) and 7.5% for downturns (peak to trough).

3. Estimate two probit models to calculate the probability of being in a peak or trough in a given quarter.

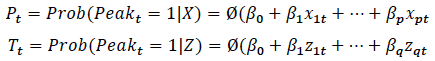
where P _t and T _t are the probability of a peak or trough and X _t and Z _t are explanatory variables which include the gap between actual prices and the time trend, the percentage change in real house prices, the number of house prices peaks in other OECD countries, borrowing conditions (the long-run level and percentage change in interest rates), and others.

Their model could classify 63 per cent of observations correctly. The power was higher for peaks (70 per cent). There were only two troughs in the 20 countries, which the model did not pick up (although the probability rose) but the model correctly classified when troughs were not occurring 91 per cent of the time.

Forecasting tax receipts directly

Rather than forecast the tax base and apply a complex tax model on top of the base, it is worth examining the forecast properties of several of the above techniques applied to LBTT receipts themselves. Technical assumption-based forecasts, univariate time series, or simple structural approaches are best suited for forecasting tax receipts directly.

Fewer resources and modelling effort are likely to be required, which may be appropriate given that LBTT is small relative to the Scottish budget. Practitioners in smaller forecasting groups mentioned that for forecasts below a threshold (such as £3 billion), they simply grow tax receipts with population and inflation, or directly in-line with nominal GDP, with no estimated parameters. Given that thresholds for LBTT are not indexed to inflation, it would be reasonable to augment this with an elasticity of revenue growth to GDP to account for fiscal drag which could be estimated over history.

If not used for the model itself, a simple growth model of receipts can be a useful check on the reasonableness of the main forecast.