The Importance for the Fish Processing and Merchanting Sector of Landinsg of Fish from the Waters of Pentland Firth and Orkney to the Local and Scottish Economies

ANNEX 2: The Concept of a Multiplier

The Structure of an Economy

While the interdependency of firms within an economy had long been understood, it was not until the 1920s that a Russian émigré, Wassily Leontief (1905-1999), working in the United States on the economics of production, realised that the accounts of firms (or more accurately groups of firms) could be placed side by side to provide a means of examining its precise nature.

It emerged that the sales of primary producers (farming, fishing, forestry, and mining) become the purchases of secondary producers (manufacturers and other processors) in a supply chain that runs downstream through the tertiary sector (broadly; services, retailing and distribution) to the final consumer.

The obverse of this is that the cost structure of the supply chain runs in the opposite direction upstream from the consumer with payments being made at each stage for the raw materials and other factors of production in the supply process.

Hence raw materials enter the supply chain at a high level while finished goods enter close to the end of the chain. Imports enter the supply chain at many different points depending on their state of finish.

Thus, throughout the supply chain, the sales of one firm are the purchases of another until the goods or services are exported or reach the domestic final consumer. However complex the pattern of trade between firms, the basic flow downstream always exists, with value being added at each stage.

The organic interdependency is graphically illustrated when a large company is forced to cease trading. Often upstream suppliers are left unpaid and purchasers downstream lose money paid for unsupplied goods. This is often sufficient to force some of the suppliers or purchasers out of business.

Table N2.1 below shows an abstract Input-Output Table known as the Consolidated Transactions Matrix.

In the real world, it is impossible to include all firms individually because of the dimensions of the table that would be created but Leontief realised that it is possible to group firms into industries or sectors.

A common practice in textbooks is to aggregate activity into the three basic sectors of an economy, primary, secondary and tertiary (see for example, an early contribution, O'Connor and Henry 1975).

The latest Input-Output Tables for Scotland for 2009 (2013) show firms grouped into 104 sectors.

Table N2.1: The Concept of the Sales and Purchases Transactions in the Supply Chain

£m	Year	Purchaser
		Firm 1	Firm 2	Firm n	Total Intermediate Demand	Households	Misc Final Demand	Exports	Total Output
Producer	Firm 1
	Firm 2
	Firm n
	Total Primary Inputs
	Households
	Imports
	Indirect Taxes & Profits
	Total Inputs

This possibility to aggregate makes it possible to isolate a particular segment or firm within an entire economy and from there to determine its contribution to that economy. It is also possible to specify the particular economy to be used, enabling regional impacts to be examined, so long as the basic data are available.

Hence, Input-Output Analysis offers a rigorous means of estimating the contribution of an economic activity to an economy as a whole (Chiang 1984, offers a lucid explanation of the methodology and underlying assumptions).

Multiplier Effects

An increase in demand (or alternatively in supply), known as the direct multiplier effect, creates organic growth within an economy because the firm experiencing the increase will itself need to purchase additional factors of production upstream and supply the additional product downstream in the supply chain.

The suppliers upstream will therefore enjoy additional demand and the purchasers will absorb the additional supply. Both will need additional resources in capital and labour to cope, creating an indirect multiplier effect.

The effects continue within the economy because the profits and wages amount to an increase in income which is spent more generally throughout the economy creating further demand and supply, and further need for capital and labour. These cycles, known as induced effects, would continue to infinity were it not for the fact that on average some income is saved and this acts as a dampener in each successive cycle.

The direct and indirect effects produce a Type I multiplier. A Type II multiplier includes direct, indirect and induced effects.

Suppose, for example, for each job in a factory a further 0.7 jobs are needed indirectly in the upstream suppliers to support the original job and a further 0.4 jobs are created (induced) in the economy as a whole to support their increased spending. The Type I multiplier is 1.7 (1 direct and 0.7 indirect jobs). The Type II multiplier is 2.1 (1 direct job plus 0.7 indirect jobs plus 0.4 induced jobs).

It can readily be seen that the multipliers have both upstream and downstream effects, and these may be separated in the calculations by treating the data from the point of view of demand or supply.

Assumptions

The multipliers show the size of the part of the economy based on the basic investment. The Technology Matrix and the Consolidated Transactions Matrix from which it is derived are linear. This implies constant returns to scale from any given levels of output, income and employment.

While the linearity is safe for small changes around the existing levels of output, income and employment, increasingly large changes mean that any non-linearity in the technology will not be observed. Hence it does not necessarily follow if the basic investment were removed, that all the employment, for example, based on it would be lost.

It is also assumed that there are supplies of all resources available including labour necessary to meet the needs of any increased investment.

The Problem of Households

A further conceptual problem arises from the question of where to place the household sector in the Input-Output Table. Households have a dual role in the economy.

The first of these roles is as a final consumer, and hence they may be included in the final consumption segment of the Consolidated Transactions Matrix. This places them outside the shaded area of inter-dependent business activity and labour income has to be included in the secondary inputs below the total of primary inputs.

This approach to the position of the household sector offers the possibility of calculating the Type I multipliers showing the direct and indirect effects of the presence of an industry. The Consolidated Transactions Matrix produced is described as Open and the expenditure of households need not equal the income from labour.

An alternative approach is to treat households as businesses which supply labour services and receive payment in return. This approach places the household sector firmly in the central shaded part of the Consolidated Transactions Matrix and offers the Type II multipliers, describing the direct and indirect effects of the Type I multiplier, and also the induced effects. The Consolidated Transactions Matrix is then said to be partially closed.

The Consolidated Transactions Matrix may be constructed so that household expenditure and labour income balance. This Closed matrix arises when savings are treated as a cost to the household business of supplying labour.

Estimation Procedure

In order to calculate, it is necessary to Constructing a Consolidated Transactions Matrix of the form shown in Table N2.1 above enables the Leontief (1951) demand-driven multipliers to be calculated. For illustrative purposes this is reduced further to Table N2.2 below and is shown, by convention, with the household sector excluded from the central core.

Table N2.2: The Consolidated Transactions Matrix

€		Purchases by
		Processing & Merchants: Orkney	Processing & Merchants: N. Highland	All Other Sectors	Final Demand	Total Output
Producer	Processing & Merchants: Orkney	x 11	x 12	x 13	d 1	x 1
	Processing & Merchants: N Highland	x 21	x 22	x 23	d 2	x 2
	All Other Sectors	x 31	x 32	x 33	d 3	x 3
	Primary Inputs	y 1	y 2	y 3
	Total Inputs	x 1	x 2	x 3

Table N2.3: The Technology Matrix

		Purchaser
		Processing & Merchants: Orkney	Processing & Merchants: N. Highland	All Other Sectors
Producer	Processing & Merchants: Orkney	a 11	a 12	a 13
	Processing & Merchants: N Highland	a 21	a 22	a 23
	All Other Sectors	a 31	a 32	a 33

From the central core (the grey shaded area) of the Consolidated Transactions Matrix, a Technology Matrix, shown above in Table N2.3, is constructed where i=1 to n and j=1 to n, where n is the number of sectors in the economy.

The elements a _i,j are the percentages of Total Input

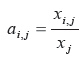
The Technology Matrix, T, shows, for example, that a unit of production of the fish processing sector requires a _1,2 units of input from the fishing sector (landed fish), a _2,2 units from the fish processing sector ( e.g. fish traded with another processor) and a _3,2 units of other products (capital equipment, energy, professional services etc.) from the rest of the businesses in the economy.

Mathematically, the model can be expressed as

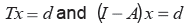
where x is the vector of outputs, d is the vector of final demand, I is the Identity Matrix and A is the matrix of input coefficients a _i,j.

If T is non-singular, the unique solution, 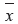, will be

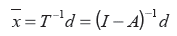
The upstream or demand-driven component of the output multiplier is the sum of each column, i, of the matrix ( I - A) ^-1 and for industry j is

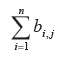
The upstream or demand-driven component of the income multiplier is the total interdependency on income, h, divided by the direct income dependency for industry j and can be expressed as

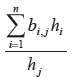
The upstream or demand-driven component of the employment multiplier is given by

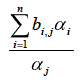
where 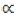is the employment coefficient defined as the employment per unit of output (in other words, the inverse of per capita productivity).

For supply-driven multipliers the elements of the Technology Matrix are the percentages of Total Output in the relevant row (Ghosh 1958) and the same approach to estimating the multipliers may then be followed.

When the household expenditure column and the household income row are included in the intermediate (shaded) sector of the Consolidated Transactions Matrix, then both the Leontief Type II and the Ghosh Type II multipliers may be estimated.

However, in summing the columns of the inverse of the Technology Matrix, ( I -A) ^-1, to obtain the output multipliers, the household row must be omitted because the objective is to measure the effect on output in the original industrial sectors.

The multipliers calculated this way may then be applied to the values of output, income and employment to be found in the original Consolidated Transactions Matrix to estimate the levels of output, income and employment dependent on the economic activity of, in this case, the Fish Processing Industry and Fish Merchants of Orkney and the Fish Processing Industry and Fish Merchants of North Highland.