Estimates of Collision Risk of Harbour Porpoises and Marine Renewable Energy Devices at Sites of High Tidal-Stream Energy

Appendix 1: Vertical Array Acoustic Monitoring of Porpoises in Loch Duich and Sound of Sleat as part of a Scottish Government Funded Project

Jamie Macaulay & Jonathan Gordon - EcologicUK Ltd.

Introduction

The underwater behaviour of small cetaceans at tidal turbine sites, and in particular the proportion of time they spend at different depths, is highly relevant to any realistic assessment of collision risk. Because tidal rapids are such physically unusual habitats we can't expect animals to behave within them in the same way as they have been observed to do elsewhere. Thus, there is no case of extrapolation using dive behaviour recorded in other locations. Underwater behaviour must be measured in tidal rapids during periods of high tidal current.

In 2009, as part of a study funded by the Welsh Assembly Government Ecologic Ltd and SMRU developed a vertical hydrophone array and a methodology for locating porpoises and measuring their depths using passive acoustics (Gordon et al., 2011). Additional work on analysing vertical array data using Markov Chain Monte Carlo localisation was undertaken by Macaulay as part of his undergraduate thesis. As part of the current project the Ecologic array was loaned to SAMS and was deployed from the HWDT research vessel Silurian. A variety of recordings of real porpoises in still waters and high tidal current areas were made and trials with test sound sources at known ranges and depths were undertaken. On the current project there was insufficient time to make definitive measurements of porpoise behaviour, however, it has served as a trial and proof of concept as well as providing the first indications of porpoise underwater behaviour in strong tidal current areas off the West Coast of Scotland.

Methods: Equipment

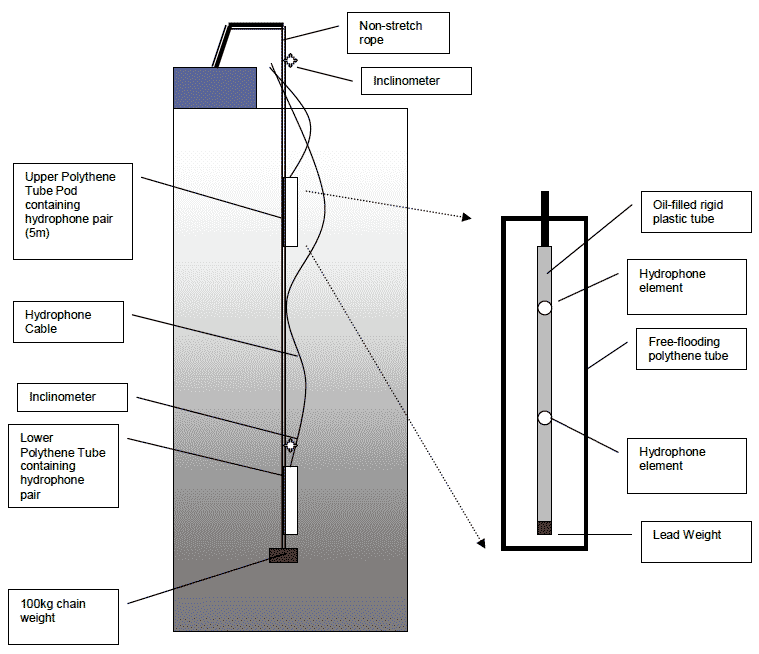
The vertical array comprised 4 individual hydrophone elements. These were configured as two pairs spaced 25cm apart with each pair separated by ~15m, see Figure 1. Each hydrophone pair was mounted in an oil-filled rigid plastic tube with a lead weight at the bottom which in turn was suspended within a free-flooding polythene cylinder. In this way, the hydrophone pairs were protected from the influence of water flow and were able to maintain a vertical orientation. Digital inclinometers attached to the suspension line just above the bottom cylinder and near the line's attachment point on the boat above water, provided information on the orientation of the cable away from the vertical. The hydrophones in the array were Magrec HP03 units which each consisted of a spherical ceramic hydrophone and a 29dB preamplifier with an integrated 2kHz high pass filter. Signals from the array were processed using Magrec HP27 ST preamplifiers to provide additional gain and a 20kHz high pass filter was applied to the amplifier output. Signals were digitised at 500kHz using two synchronised National Instruments 6251 USB DAQ devices. Software to achieve this synchronisation was written by Douglas Gillespie and implemented in the PAMGUARD acoustic monitoring program.

Figure 1. Four element vertical hydrophone array used for determining depth of porpoise vocalisations.

Data Analysis

Raw sound files were first analysed using click detector routines in PAMGUARD which was configured with each pair of hydrophones were treated as a paired channel. The click detector parameters applied were based on those typically used for detecting and classifying harbour porpoise clicks. The waveforms of these clicks, along with timestamps and information on the sampling rate and soundcard settings were packaged into .clk files (the format used by Rainbow Click). The recorded wav files from each hydrophone were run through PAMGUARD to detect likely porpoise clicks and a specially written Java program was then used to identify probable corresponding clicks on different hydrophones and localise using the MCMC techniques discussed below. (See Gordon et al. 2011 for details of the program).

Markov Chain Monte Carlo Localisation Method- Theory

An array of four or more hydrophones can localise in three-dimensional space. In this case practical considerations related to the feasibility of maintaining a complex array configuration in strong tidal currents led us to the use of a simpler vertical array consisting of two hydrophone pairs. Although the required number of hydrophones for three-dimensional localisation was met by this, the linearity of the array results in degeneracy of position after localisation so that only range and depth information are provided. In the case of a click incident on a single pair of hydrophones, the only information that can be extracted is the bearing to the sound source (porpoise). This bearing is resolved in three-dimensional space as a cone of possible of locations. The porpoise can be located anywhere on the surface of this cone; and the length of the cone is unknown. When a second pair of hydrophones is introduced, a second cone results. The intersection of these two conical surfaces indicates the position of the porpoise. For a three-dimensional array of four hydrophones there are six possible cones and there will generally be only one crossing point, providing a three-dimensional point localisation. However, because of the symmetry of the vertical array the cones always cross each other in perfect alignment, resulting in a ring of possible locations centred on the array. ( Fig. 2). Therefore, if the linear array is vertical both depth and range are determined.

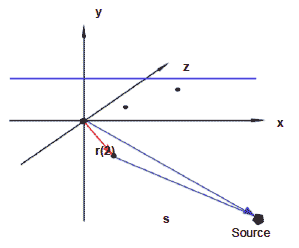
Time of arrival delays were calculated for each hydrophone using a combination of PAMGUARD and custom Java script (see above) and a Markov Chain Monte Carlo Algorithm was then utilised to localise each click. Markov Chain Monte Carlo is a statistical method widely used in physics and astronomy. Figure 2 shows multiple hydrophones represented by black dots in three-dimensional space. r( i) and s represent the vectors from the origin to hydrophone i and the source respectively. Considering distance=speed x time this leads to the equation

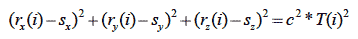
where c is the speed of sound, T(i) is the total time from the source to hydrophone i with r _x/y/z and s _x/y/z the Cartesian components of r and s. Rearranging this yields .

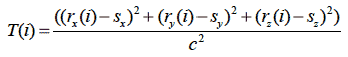
This significance of this equation is that it allows calculation of the expected time delays between the hydrophone elements for a simulated source located anywhere in space.

Figure 2. Vector diagram showing distance from source to hydrophone 2 in 3D space. Black dots represent hydrophones and hydrophone 1 is located at the origin.

Although straight forward this forms the basis of Markov Chain Monte Carlo localisation- from now on referred to as MCMC. MCMC localisation works by assuming a location in space and calculating the χ ² of that location using.

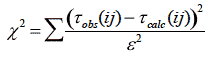
where τ _obs (ij) is the actual observed time delay between hydrophones i and j and τ _calc (ij) is the calculated time delay between hydrophones i and j from an acoustic source if it was at the assumed location. ε represents the expected error in observed data. For a four hydrophone array i=1,1,1,2,2,3 and j=2,3,4,3,4,4.

If χ ² is lower at the new location the jump is deemed successful and the new location is adopted. If χ ² is not lower then the jump is only accepted as successful with a probability of

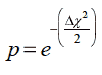
where represents the difference in χ ² values between the previous and new jump point. If still unsuccessful the new location is discarded and another random jump calculated from the previous location. If successful then a new random jump is instigated from the new location. In this way a chain of successful jumps results, converging quickly to the likely porpoise location. Once close to this location the chain then jumps around it creating a cloud of points, the density of which represents a probability distribution of the porpoise position.

The power of this technique is that it provides a reliable measure of the probability distribution for location and it can also easily incorporate other unknown parameters, in addition to the location of the porpoise. In the case of the vertical array for example, it is possible to allow the chain to search for unknowns in the position of the array.

Compensating for cable angle

Although inclinometers were included in the array they provided incomplete information on the array position. The inclinometer located on the top of the array was manually kept aligned with the bow of the survey vessel and thus provided exact information on the orientation of the top of the cable. However, due to the twist in the cable the orientation of the bottom inclinometer was not known and it therefore provided information on the angle of tilt but not its orientation. The orientation of the cable connecting both hydrophones is completely unknown. If one assumes inclination angles of Θ and azithumal angles of Φ ( Fig. 3) then there are three unknowns, Θ ₂,Φ ₂ and Φ ₃. Plotting the inclination angles, Θ ₁ and Θ ₃ it is evident that a periodic variation in angle occurred.

Figure 3. Diagram of the vertical array with an exaggerated offset angle. The shaded rectangles each represent a hydrophone pair. The red lines indicate the inclination angles Θ ₁, Θ ₂ ,Θ ₃ and circles represent the resultant possible azimuthal components due to unknown direction and inclination of the cable. The co-ordinate axis represented the Cartesian co-ordinate system used throughout the project.

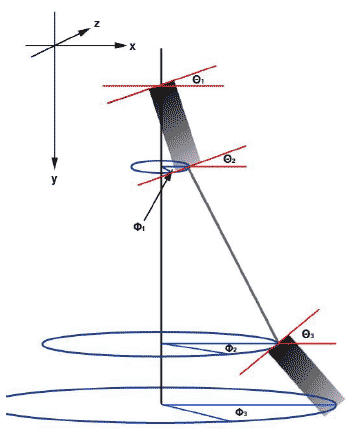
Figure 4. Inclination angles of the array over time May18 2010. Red represents to top inclinometer and blue represents the bottom inclinometer. Time is in matlab datenum format which converts date/time in a single number starting at 0 on Jan 0000 00:00:00 .

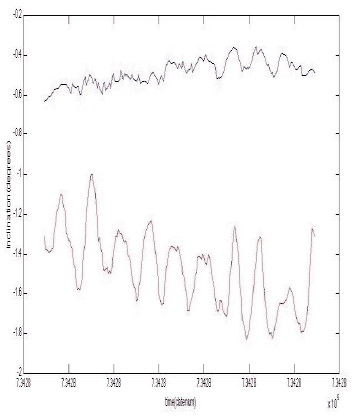
This periodic motion is attributed to the roll of the vessel and therefore it can be assumed that movement in the array is mostly in one plane. Thus the unknowns, Φ ₁ and Φ ₂, can be eliminated leaving Θ ₂, the inclination of the cable, as the last unknown parameter. The Markov Chain therefore calculates a random position in space and a random value for Θ ₂ on every jump.

Implementation

The method was implemented as a Java program. The test for a successful MCMC localisation is to determine whether several (in our case we used ten) different Markov chains all converge to the same probability distribution. The first 65% of each chain was discarded to remove effects from the initial starting locations and the mean and standard deviation of the depth and range of the remaining jumps calculated.

Final data was output to a spreadsheet showing time, depth and range along with errors for each localised click.

Field Calibration Trials
Methods

A porpoise click generator was used to broadcast simulated porpoise clicks to test the performance of the vertical array system. The click generator consisted of a 12V Sony XPLOD 1200W Car Audio Amplifier (XM-2200GTX) driving an HS150 hydrophone (Sonar Research & Development Ltd, Beverley, UK). The broadcast signal was a .wav file comprising a wave train of twenty simulated porpoise clicks created in MATLAB and this was output to a National Instruments 6251 DAQ card using a laptop computer. (We are grateful to Jay Barlow, NOAA Southwest Fisheries Centre, USA, for suggesting this playback equipment to us.)

The broadcast equipment was deployed from a drifting inflatable dinghy at a series of ranges of between 50 and 350m from the research vessel which was also drifting. At each range the transmission hydrophone was deployed at four different depths 2.5, 5, 7.5 and 10m. Range was measured using laser range finding binoculars accurate to 0.5m. The depth of the transmitting hydrophone was recorded using a UWATEC Aladdin prime dive computer accurate to 0.1m.

The vertical array was configured with hydrophones at water depths of 4.77, 5.13, 18.13 and 18.38 m and kept taut with a 100 kg weight.

Results

Although all broadcast click trains (out as far as 350m) were detected on a computer running PAMGUARD on the survey vessel, it was found that recordings that could be analysed to provide reliable range and depth measurements were collected at only five of these ranges. We suggest reasons for this below. Generally however, the results of the calibration are encouraging. Figure 5 summarises data for acoustically derived depth measurements. For transmission depth of 7.5m and deeper localizations were usually successful but, during this trial, depths were not calculated successfully for shallower transmissions. As Figure 6 indicates there is a good agreement in range measurements for distances out to 127m. At greater ranges, of 250 and 350m however, there were only sporadic detections from which a range could be calculated and these were not accurate.

Figure 5. Depths calculated during calibration trials. Red triangles are the mean depth vale for all MCMC chains in each successful location. The error bars show the standard deviation of the MCMC probability density cloud.

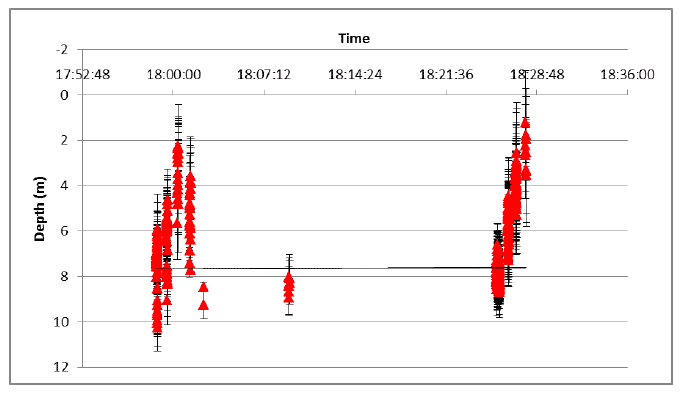
Figure 6 . Depths calculated during calibration trials. Red triangles show the mean all calculated depths for each calibration station. The mean depth for the same station calculated using the dive computer data are show as blue diamonds.

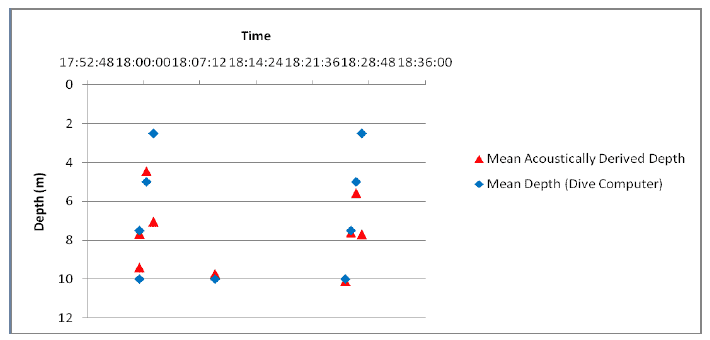
Figure 7. Depths calculated during calibration trials. Red triangles are the mean depth value for all MCMC chains in a successful localisation and error bars represent the standard deviation of the MCMC probability density cloud.

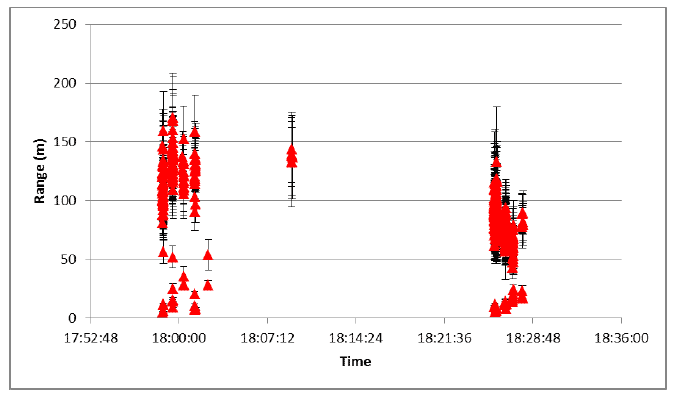
Figure 8. Range data from calibration trials. Red triangles are the mean range for all acoustic locations at a calibration station the mean of ranges measured using laser range finding binoculars as shown as blue diamonds.

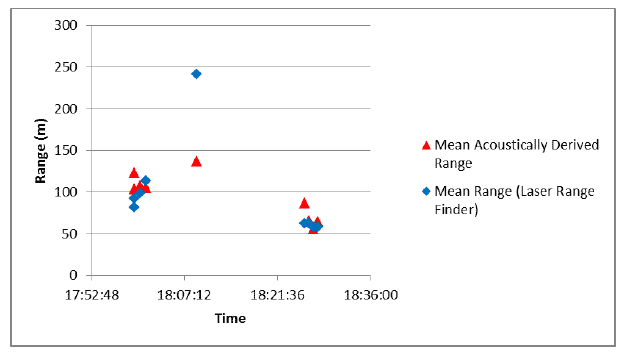
Table 1 Ranges and depths of broadcast hydrophone during calibration trials

Time	Distance from Boat(m)	Depth of Hydrophone (m)
18:57:32	82	10
18:58:43	92	10
18:59:28	98	7.5
19:00:24	113	5
19:01:01	127	2.5
19:08:03	241	10
19:09:24	245	7.5
19:10:32	248	5
19:11:24	247	2.5
19:17:12	350	10
19:18:20	350	7.5
19:19:04	351	5
19:20:16	349	2.5
19:25:51	62	10
19:25:52	62	10
19:26:54	61	7.5
19:27:23	59	5
19:27:45	58	5
19:28:20	58	2.5

These trials indicate that within the range tested (7.5-10 m broadcast depth and 50-125 m), the method provided accurate results with good precision and no indications of bias. There are grounds for expecting that results at greater ranges might be better with real porpoise in typical field conditions.

Field Recordings of Porpoises and Dive Profiles

Extended recordings were made from the vessel drifting in still waters in Loch Duich on (15/05/2011 and 17/05/2011) and in tidal currents in the upper Sound of Sleat (18/05/2011). On both occasions porpoises were sighted in the recording locations though in the Sound of Sleat porpoises were often detected acoustically without being seen.

Figure 9 shows a histogram of all acoustically derived depths from vertical array recordings of harbour porpoise made during this project. This provides a first indication of the use animals make of the water column in these habitats.

Figure 9. Histogram of acoustically derived depths for all acoustic encounters.

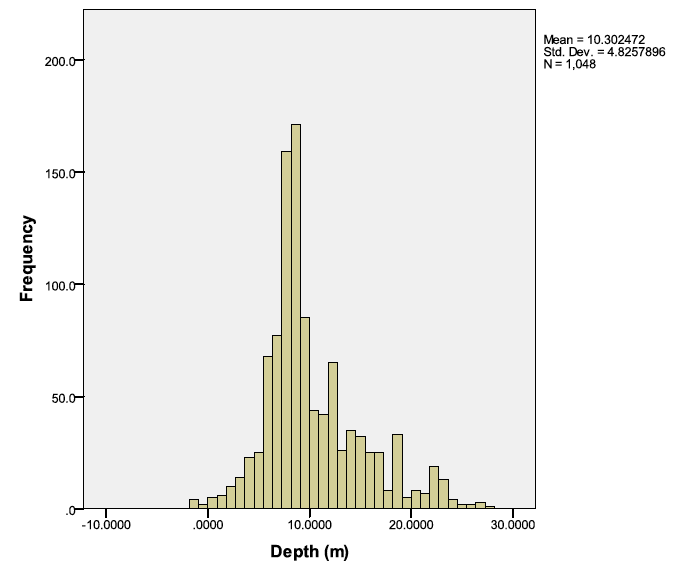
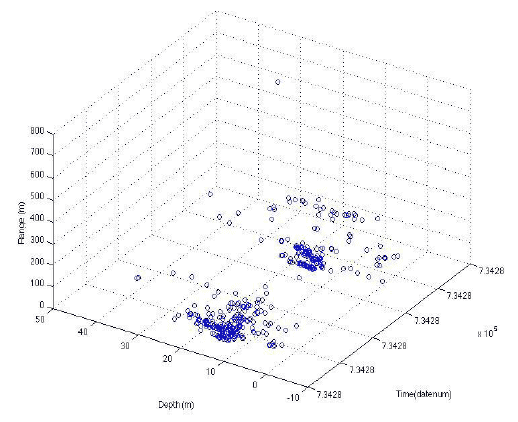
Figure 10 is an example fine-scale plot of range, depth and time. This shows a clear clustering demonstrating the correlation between all three variables - what is expected for dive profiles.

Figure 10. Example plot of Time v Depth v Range - May 18th. Note that time is in Matlab datenum format and depth and range are in meters.

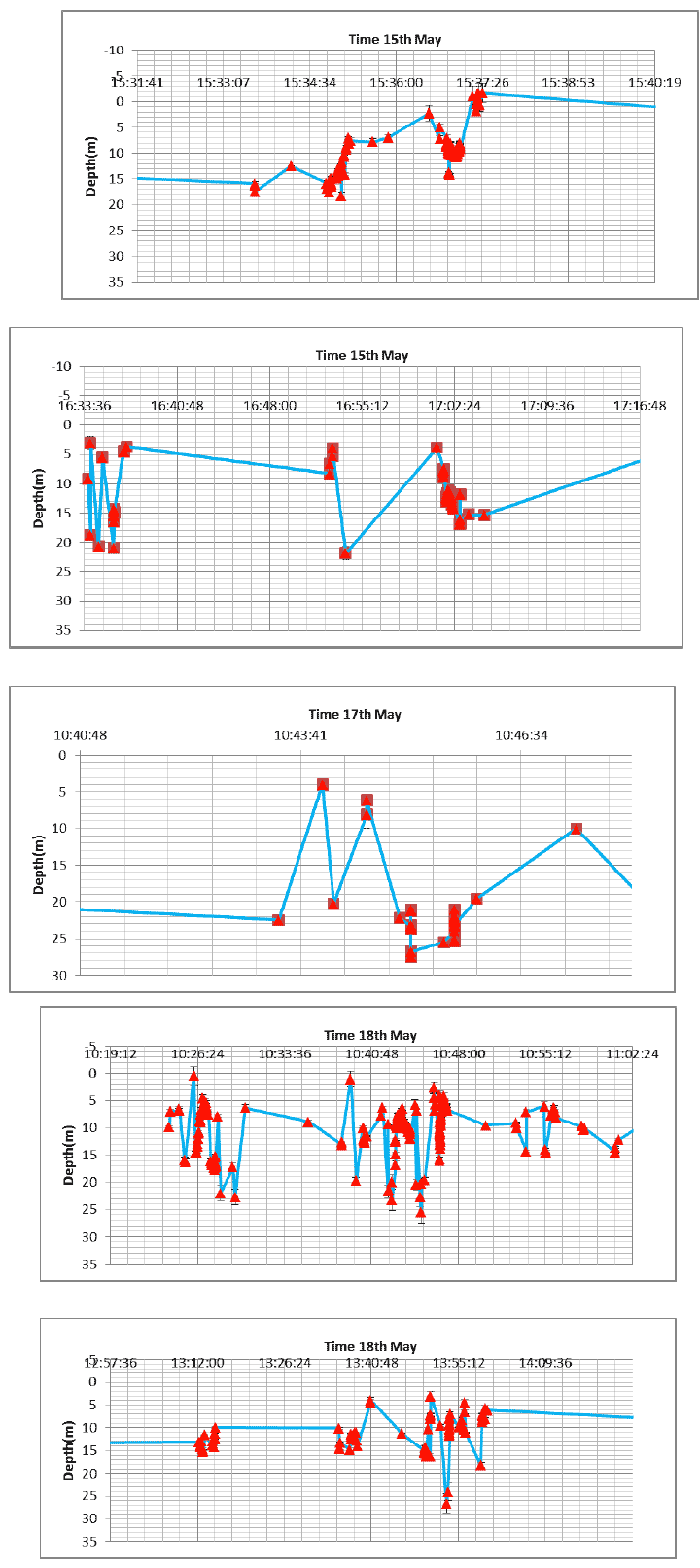
Figures 11 and 12 show the locations of the research vessel, in Loch Duich and the Sound of Sleat respectively, at times when acoustic localisations were made in. Circles around these plots show them maximum range calculated during each sequence of locations. Although, as explained above, the location of porpoises cannot be calculated with a vertical array, it is likely that they were within these circles. A series of detailed plots of depth calculated using MCMC method against time which provide indications of dive profiles for individual dives are shown in Figure 13. These appear to show dives with durations of around 90-120 seconds and with dive depths of between 5 and 15 m. (The time on these plots can be cross referenced with the times shown next to locations in Figures 11 and 12 to determine the position of the boat during particular sequences.)

Clearly, depths can only be calculated when an animal vocalises, so these profiles will inevitably be patchy and incomplete. Here we have plotted profiles by simply linking calculated depths. An alternative approach would be to fit a line to these points statistically. These plots largely serve to demonstrate the future potential of the method to provide detailed information on underwater behaviour in area with high tidal currents which is highly relevant to quantifying collision risk. It is interesting to note that in these data porpoise are rarely, if ever, diving to the bottom as has been reported in other studies. If this is typical of their behaviour in these habitats then the risk of collision with turbines sited deep in the water column would be reduced. However, we emphasise that a larger effort will be needed in the future to provide reliable and representative biological information.

Figure 11. Locations and times at which porpoise acoustic depth data were calculated from vertical array recordings in Loch Duich on 15th and 17th of May 2010. (Dates are shown only for the 17th of May locations, which are furthest east.) Circles are indicative of maximum range for each location.

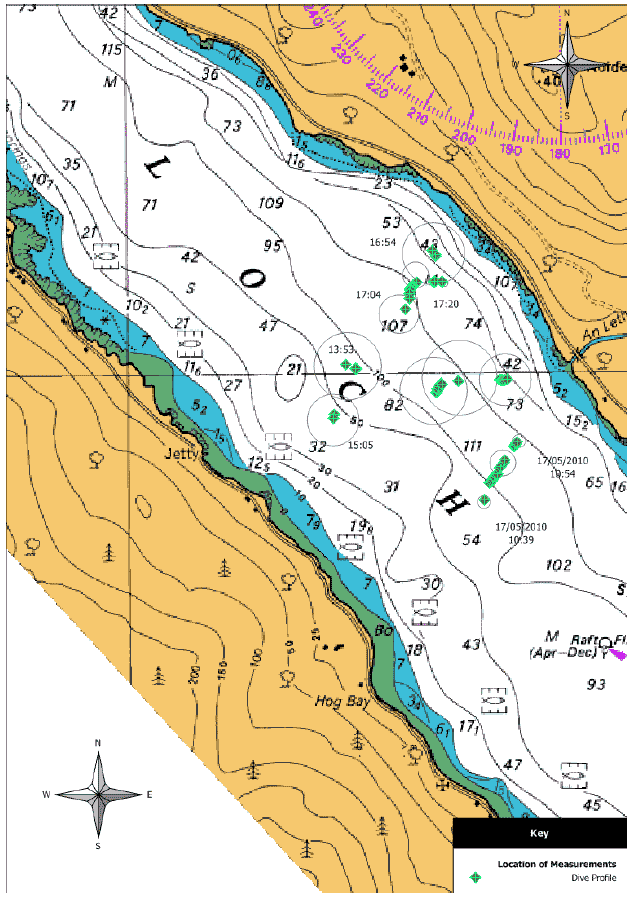
Figure 12 Locations and times at which porpoise acoustic depth data were calculated from vertical array recordings in the upper Sound of Sleat south of Kyle Rhea on the 18th of May 2010.

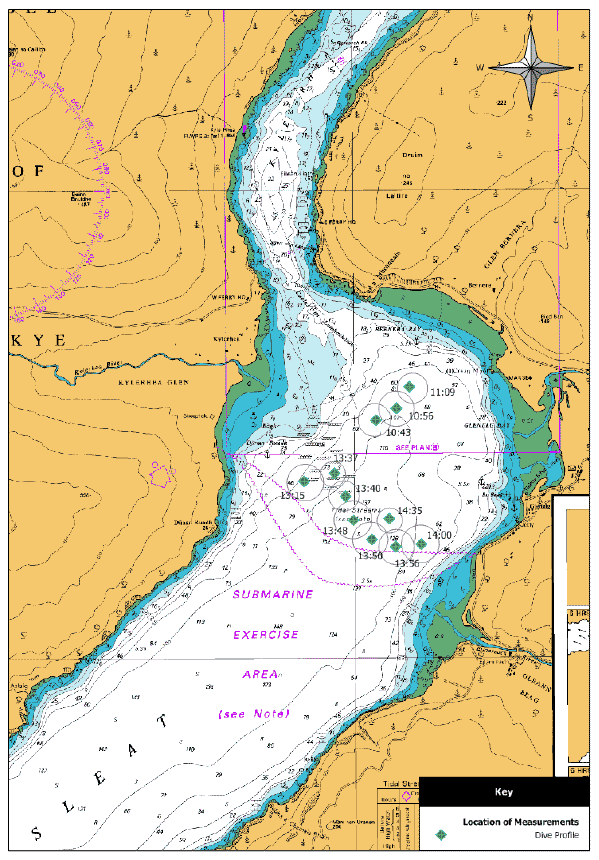
Figure 13. Plots of acoustically derived depth vs time giving an indication of dive profiles

Reference

Gordon, J., D. Thompson, R. Leaper, C. Pierpoint, S. Calderan, J. Macaulay, and T. Gordon. 2011. Studies of marine mammals in Welsh high tidal waters. N. Simpson, editor. Welsh Assembly Government. 152pp.