Scotland's Fiscal Outlook: The Scottish Government's Medium-Term Financial Strategy

Annex A - Assessing forecast error risk to the Scottish Budget

The Scottish Government has developed a framework for performing risk analysis on the likelihood, direction and magnitude of reconciliations payments for forecast errors over time. The framework developed in this analysis provides a tool that allows for insights into what the key drivers of forecast error risk are and to assess the capacity for the Scottish Government to be able to deal with it.

Methodology

The framework to analyse reconciliation risk takes advantage of a technique called a Monte Carlo Simulation. This technique is often used to help understand and quantify the impact of risk and uncertainty across a variety of fields and professions such as in finance, project management and forecasting.

These simulations allow the user to perform risk analysis by building models of possible results by substituting a range of values – a probability distribution – for any factor that has inherent uncertainty in it. In the case of reconciliation risk analysis, the factor of concern is the inherent uncertainty around the forecast performance of the SFC and OBR.

Forecasting performance generally refers to information on an individual’s or institution’s forecast error – the difference between what was forecast and what then eventually happened.

It is worth iterating that economic forecasting is notoriously challenging. Even with excellent data and judgements, economies are inherently difficult to forecast. For example, a working paper from the International Monetary Fund (IMF) in 2018 noted that globally, economists had failed to predict 148 of the last 153 global recessions^[46]. This was judged to be partly because the world is getting more inter-linked and complex, making accurate forecasts of individual economies increasingly difficult.

Unexpected events such as Global Financial Crises or Global Pandemics also exemplify the inherent difficulty faced by economic forecasters.

Given this, it is virtually certain that over time both the OBR and SFC are likely to have forecast errors. This is not a reflection or judgement on either institution, rather it is simply a standard reality for any forecaster.

In the Scottish Fiscal Framework it is the forecast errors of the SFC and OBR that drive the subsequent reconciliation risk faced by the Scottish Government. It is important how both forecasters have performed and how related their performance is which can have significant effects on the level of reconciliation risk involved. Consequently, four characteristics of the OBR and SFC’s forecast performance determine overall reconciliation risk. The first three are:

1. Each institution’s average forecast error over time.

2. The variance of each institution’s forecast errors over time.

3. The distribution of each institution’s forecast errors over time.

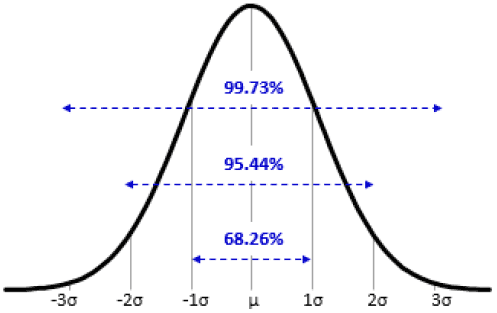
These are standard statistical properties. For example the below is a representation of a Standard Normal Distribution, with mean μ and Standard Deviation σ (the square of which is equal to the variance). These properties tell us things like what the average, or “most likely” outcome is over time (the mean μ), and the standard deviation and/or variance, provide a measure of how spread out from the mean observations tend to be over time.

The distribution can be thought of as the pattern of the forecast errors observed. For example, it might be expected that the forecast error is sometimes positive, and sometimes negative each with broadly the same respective probability which a normal distribution such as below can represent if the mean is equal to 0. Alternatively there may be reason to believe that it is more likely for forecast errors to be skewed in one direction, in which case other types of distributions can better capture this relationship.

The fourth characteristic required is:

4. The correlation (or covariance^[47]) between each institutions forecast errors over time

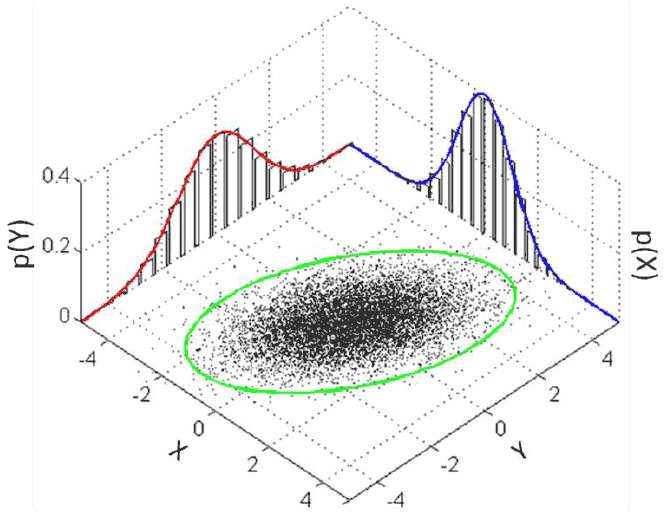
If the SFC and OBR’s forecast errors have a degree of positive correlation, then on average, when the SFC or OBR have been too optimistic (or pessimistic) in their forecasts, it is likely that the other institution was similarly too optimistic (or pessimistic) at the same time. For example, Chart A2 below is a diagram showing a hypothetical joint distribution where there is a degree of positive correlation between two distributions (the elliptical skew to the green circle). Had there been zero correlation between the two distributions, the green line would be perfectly circular.

The reason the degree of correlation or covariance is needed is because reconciliations are a function of both institution’s forecast performance over time. Whether or not the OBR and SFC’s forecasts tend to be right or wrong in a similar direction and magnitude can actually have quite a large impact on the degree of reconciliation risk implied.

These four characteristics above (the average, variance, distribution and correlation of each institution’s forecast error) can then be used to populate the assumptions required to perform Monte Carlo Simulations in order to quantify the risk and uncertainty the Scottish Government could face from forecast error for a specific tax or social security.

Consequently, as long as it is possible to populate the hypothetical forecast errors for a given scenario, it is then also possible to calculate what the subsequent reconciliation risk would be.

Monte Carlo Simulations follow the above procedure by simulating the hypothetical forecast errors using probability distributions. These probability distributions represent the likelihood and uncertainty of the future OBR and SFC forecast errors and also allow the possibility to repeatedly “sample” or “draw” from these probability distributions. The reconciliation payment for each sample or draw is then calculated resulting in a probability distribution of reconciliation risk.

For example, taking a non-informative assumption that both the SFC and OBR’s forecast errors have a normal distribution, with an average forecast error of 0%, a variance of 1% and have zero correlation / covariance with one another.

Using the above assumptions is it then possible to draw many samples (100,000 samples are used for each scenario in this paper) from this joint distribution such as below in Chart A3.

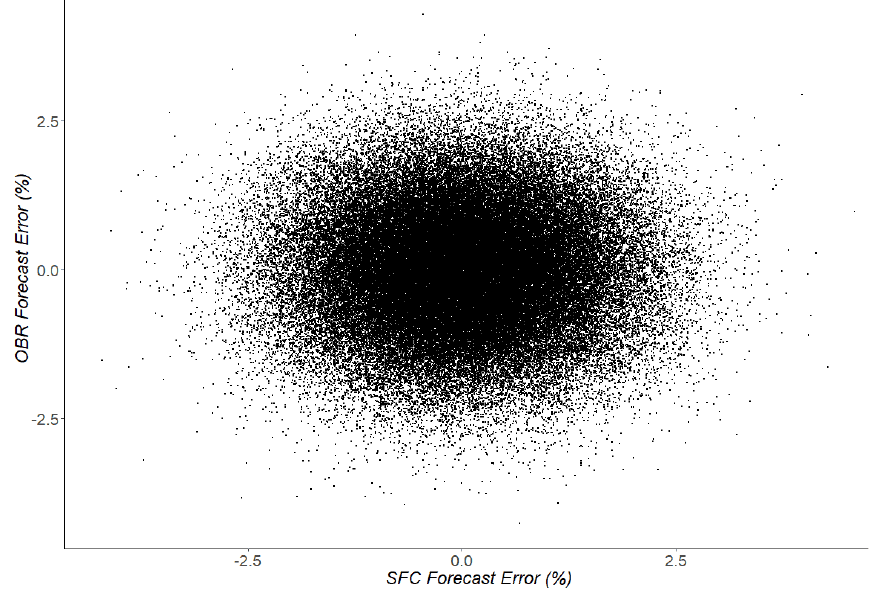
Each dot on Chart A3 represents a sample from this probability distribution, with each one representing a sample with an SFC forecast error, and a relative OBR forecast error.

Each one of these many thousands of samples can then be used to calculate a reconciliation value that would occur were these errors to occur in reality. Consequently, it is possible to create a probability distribution of reconciliation risk that allows us to quantify and assess what the average or likely reconciliation payment may be. The above example is visualised below in Chart A4, which is based on the 2018-19 Budget forecasts (from both the SFC and OBR) on devolved non-savings, non-dividends Income Tax.

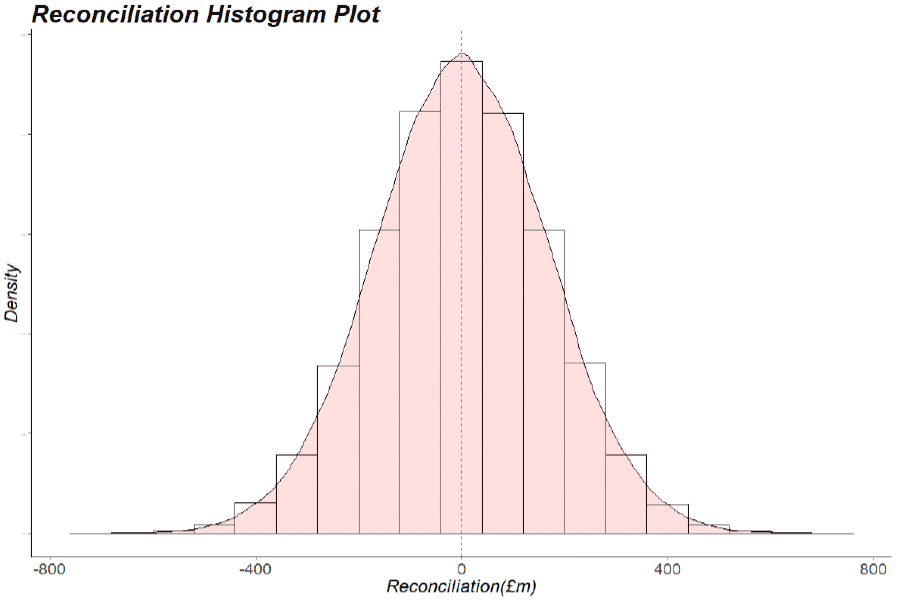
This represents a simulated probability distribution of reconciliation risk based on the assumption that both the OBR and SFC’s forecast errors have i) no correlation with each other, ii) both have an average forecast error of 0% iii) both have a forecast error variance of 1% and iv) their forecast errors have a joint-normal distribution.

Under this example scenario, because of the symmetry in each institutions forecasting performance, over time it would be expected that the positive and negative reconciliations even out, with a long-term average reconciliation payment of close to zero. However, year-on year there is likely to be volatility and, conditional on the forecast assumptions under this scenario, it would be expected that 80% of the time reconciliation payments would lie between negative £209 million and positive £211 million. Furthermore it is expected, that just over 3% of the time, reconciliations would exceed the -£300m borrowing limit currently available to the Scottish Government to deal with forecast error.

This demonstrates the strengths of Monte Carlo Simulations, with the ability to quantify the magnitude, direction and likelihood of an outcome from an inherently uncertain factor.

A central simulation on Income Tax Reconciliation Risk

Using the above methodology, it is then possible to construct a central estimate of Reconciliation Risk as a results of devolved Non-Saving, Non-Dividend Income Tax forecast error. It is not possible to know with complete certainty what the long-term forecasting performance of either the SFC or the OBR could be. However, it is possible to populate the required assumptions with any prior information available about what either institution’s forecast performance may be.

One approach to this is to assume that the SFC’s future forecasting performance is likely to be similar to that of the OBR’s to date. The OBR rather helpfully maintain and publish a historical forecast database, which tracks all historical forecasts and the eventual outturn (if available)^[48]. This includes revenue forecasts, of which there are historic forecasts of Income Tax revenue (ITR) receipts for the UK.

In the Scottish Fiscal Framework, it is the forecast of non-savings, non-dividend Income Tax Liabilities for the rUK and Scotland that is important and hence not directly comparable to the OBR’s historic forecast performance of UK Income Tax Receipts. However, the two are likely to be strongly correlated, with similar factors driving the forecast performance of each series over time (earnings assumptions, employment assumptions, Income Tax policy, etc.). Therefore, although not directly comparable, there should still be very useful information in the historic performance that can be used to update the assumptions about the OBR’s possible longer-term forecasting performance of rUK NSND Income Tax Liabilities based on how well they have forecast UK Income Tax Receipts.

Using the OBR’s historic performance, and taking a “3-Year Forecast relative to the latest available Outturn Data available at the creation of each forecast, the assumption made is that both institutions could have an average forecast error of 5.2%; a forecast error variance of 6.8% and have a positively skewed distribution, which will be characterised by a multivariate Log-Normal Distribution. The choice of distribution reflects the fact that the vast majority of the OBR’s forecast errors for Income Tax have been positive with a long right hand tail and hence may be better represented by a Log-Normal Distribution relative to a Normal Distribution. However, as a form of sensitivity analysis the results are tested using both a Multivariate Log-Normal and a Multivariate Normal Distribution and the choice of distribution does not radically alter the results. If anything the Log-Normal Distribution is actually more conservative and tends to marginally lower the risk profile.

Using the historic OBR forecasting performance, it is then possible to populate the assumptions for both the SFC and OBR’s average, forecast error, the variance of the forecast error and the type of distribution. However, the one part of each institutions forecasting performance for which there is more uncertainty on, is the likely magnitude and direction of correlation between both institutions.

In general, the greater the degree of positive correlation between the two institutions’ forecast errors, the lower the degree of forecast error risk. Conversely, the greater the degree of negative correlation the greater the degree of forecast error risk.

There are arguments that the forecasting performance of the OBR and SFC could likely have a degree of positive correlation over time. For example it may be expected that many unforeseen macroeconomic shocks (such as an unexpected change in monetary policy) are likely to affect both the Scottish and UK economies and hence influence OBR and SFC forecast errors in a similar direction.

However, given the uncertainty around the magnitude of this correlation however, a range is instead taken. In this case, the central scenario assumes a degree of positive correlation of between +20% to +80%.

Consequently, assuming that the SFC’s Income Tax forecasting performance follows a similar pattern to that of the OBR’s to date outlined above, and assuming a relatively wide range of positive correlation between the SFC and OBR’s forecasting performance, then a central estimate is that there could be a 5% to 17% probability of negative Income Tax reconciliations exceeding -£300 million.

This central estimate is based on relatively conservative assumptions. As noted, any assumption on positive correlation reduces reconciliation risk and this central estimate only assumes that there is a degree of positive correlation and no chance of a negative correlation, which is potentially quite a strong assumption.

Likewise, the assumption that the SFC and OBR have perfectly symmetrical forecasting performances is also quite strong. Depending on the degree of asymmetry, this could further negatively exacerbate the reconciliation risk that may be expected as a result of forecast error.

Overall though, there is evidence that on devolved Income Tax alone, there is a relatively high probability that forecast error in a given year could be sufficiently large enough to overwhelm the current borrowing powers provided to the Scottish Government to deal with them.

This is based on quite conservative assumptions. It is possible that by making relatively small adjustments to the underlying assumptions that the estimated risk profile is significantly larger.

The risk profile will also inevitably become worse over time as the scale of the economy and tax revenues increase whilst the borrowing powers remain fixed in nominal terms.